Chapter 3 Pursuing Low-Dimensionality via Lossy Compression

In this chapter

Entropy Minimization and Compression
Entropy and Coding Rate Differential Entropy Minimizing Coding Rate
Compression via Denoising
Diffusion and Denoising Processes Learning and Sampling a Distribution via Iterative Denoising
Compression via Lossy Coding
Necessity of Lossy Coding Rate Distortion and Data Geometry Lossy Coding Rate for a Low-Dimensional Gaussian Clustering a Mixture of Low-Dimensional Gaussians
Maximizing Information Gain
Linear Discriminative Representations The Principle of Maximal Coding Rate Reduction Optimization Properties of Coding Rate Reduction
Summary and Notes
Exercises and Extensions

“We compress to learn, and we learn to compress.”
— High-dimensional Data Analysis, Wright and Ma, 2022

In Chapter 2, we have shown how to learn simple classes of distributions whose supports are assumed to be either a single or a mixture of low-dimensional subspaces or low-rank Gaussians. For further simplicity, the different (hidden) linear or Gaussian modes are assumed to be orthogonal or independent¹¹1Or can be easily reduced to such idealistic cases., as illustrated in Figure 2.4. As we have shown, for such special distributions, one can derive rather simple and effective learning algorithms with correctness and efficiency guarantees. The geometric and statistical interpretation of operations in the associated algorithms is also very clear.

In practice, both linearity and independence are rather idealistic assumptions that distributions of real-world high-dimensional data rarely satisfy. The only thing that we may assume is that the intrinsic dimension of the distribution is very low compared to the dimension of the ambient space in which the data are embedded. Hence, in this chapter, we show how to learn a more general class of low-dimensional distributions in a high-dimensional space that is not necessarily (piecewise) linear.

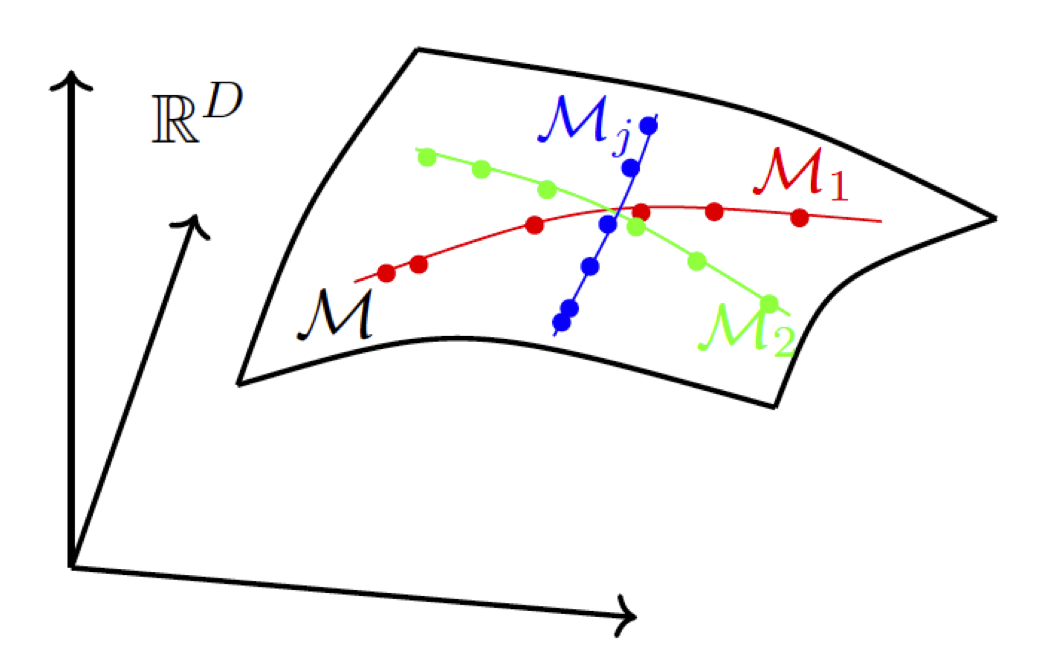
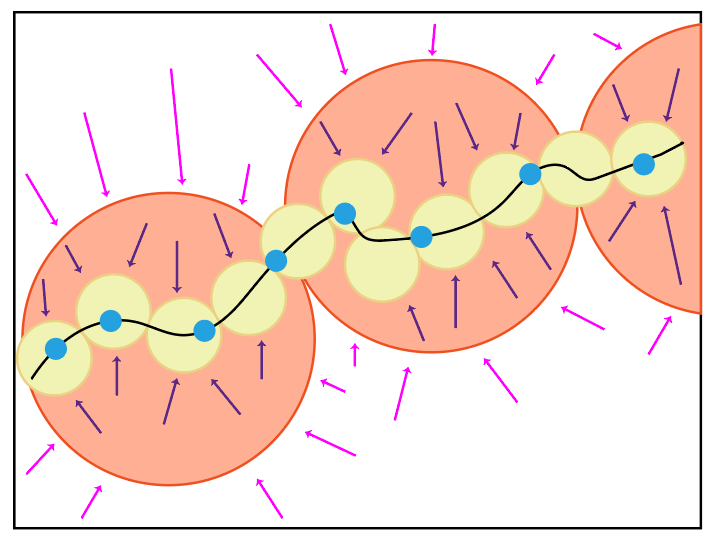
It is typical that the distribution of real data often contains multiple components or modes, say corresponding to different classes of objects in the case of images. These modes might not be statistically independent and they may even have different intrinsic dimensions. It is also typical that we have access to only a finite number of samples of the distribution. Therefore, in general, we may assume our data are distributed on a mixture of (nonlinear) low-dimensional submanifolds in a high-dimensional space. Figure 3.1 illustrates an example of such a distribution.

To learn such a distribution under such conditions, there are several fundamental questions that we need to address:

•

What is a general approach to learn a general low-dimensional distribution in a high-dimensional space and represent the learned distribution?
•

How do we measure the complexity of the resulting representation so that we can effectively exploit the low dimensionality to learn?
•

How do we make the learning process computationally tractable and even scalable, as the ambient dimension is usually high and the number of samples typically large?

As we will see, the fundamental idea of compression, or dimension reduction, which has been shown to be very effective for the linear/independent case, still serves as a general principle for developing effective computational models and methods for learning general low-dimensional distributions.

Due to its theoretical and practical significance, we will study in greater depth how this general framework of learning low-dimensional distributions via compression substantiates when the distribution of interest can be well-modeled or approximated by a mixture of low-dimensional subspaces or low-rank Gaussians.

Figure 3.1 : Data distributed on a mixture of low-dimensional submanifolds ∪ j ℳ j \cup_{j}\mathcal{M}_{j} ∪ start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT caligraphic_M start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT in a very high-dimensional ambient space, say ℝ D \mathbb{R}^{D} blackboard_R start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT . — Figure 3.1: Data distributed on a mixture of low-dimensional submanifolds $\cup_{j}\mathcal{M}_{j}$ in a very high-dimensional ambient space, say $\mathbb{R}^{D}$ .

3.1 Entropy Minimization and Compression

3.1.1 Entropy and Coding Rate

In Chapter 1, we have mentioned that the goal of learning is to find the simplest way to generate a given set of data. Conceptually, the Kolmogorov complexity was intended to provide such a measure of complexity, but it is not computable and is not associated with any implementable scheme that can actually reproduce the data. Hence, we need an alternative, computable, and realizable measure of complexity. That leads us to the notion of entropy, introduced by Shannon in 1948 [Sha48].

To illustrate the constructive nature of entropy, let us start with the simplest case. Suppose that we have a discrete random variable that takes $N$ distinct values, or tokens, $\{\bm{x}_{1},\ldots,\bm{x}_{N}\}$ with equal probability $1/N$ . Then we could encode each token $\bm{x}_{i}$ using the $\log_{2}N$ -bit binary representation of $i$ . This coding scheme could be generalized to encoding arbitrary discrete distributions [CT91]: Given a distribution $p$ such that $\sum_{i=1}^{N}p(\bm{x}_{i})=1$ , one could assign each token $\bm{x}_{i}$ with probability $p(\bm{x}_{i})$ to a binary code of size $\log_{2}[1/p(\bm{x}_{i})]=-\log_{2}p(\bm{x}_{i})$ bits. Hence the average number of bits, or the coding rate, needed to encode any sample from the distribution $p(\cdot)$ is given by the expression:²²2By the convention of Information Theory [CT91], the $\log$ here is to the base $2$ . Hence entropy is measured in (binary) bits.

H(\bm{x})\doteq\mathbb{E}[\log 1/p(\bm{x})]=-\sum_{i=1}^{N}p(\bm{x}_{i})\log p(\bm{x}_{i}).

(3.1.1)

This is known as the entropy of the (discrete) distribution $p(\cdot)$ . Note that this entropy is always nonnegative and it is zero if and only if $p(\bm{x}_{i})=1$ for some $\bm{x}_{i}$ with $i\in[N]$ .³³3Here notice that we use the fact $\lim_{p\rightarrow 0}p\log p=0$ .

3.1.2 Differential Entropy

When the random variable $\bm{x}\in\mathbb{R}^{D}$ is continuous and has a probability density $p$ , one may view that the limit of the above sum (3.1.1) is related to an integral:

h(\bm{x})\doteq\operatorname{\mathbb{E}}[\log 1/p(\bm{x})]=-\int_{\mathbb{R}^{D}}p(\bm{\xi})\log p(\bm{\xi})\mathrm{d}\bm{\xi}.

(3.1.2)

More precisely, given a continuous variable $\bm{x}$ , we may quantize it with a quantization size $\epsilon>0$ . Denote the resulting discrete variable as $\bm{x}^{\epsilon}$ . Then one can show that $H(\bm{x}^{\epsilon})+\log(\epsilon)\approx h(\bm{x})$ . Hence, when $\epsilon$ is small, the differential entropy $h(\bm{x})$ can be negative. Interested readers may refer to [CT91] for a more detailed explanation.

Example 3.1 (Entropy of Gaussian Distributions).

Through direct calculation, it is possible to show that the entropy of a Gaussian distribution $x\sim\mathcal{N}(\mu,\sigma^{2})$ is given by:

h(x)=\frac{1}{2}\log(2\pi\sigma^{2})+\frac{1}{2}.

(3.1.3)

It is also known that the Gaussian distribution achieves the maximal entropy for all distributions with the same variance $\sigma^{2}$ . The entropy of a multivariate Gaussian distribution $\bm{x}\sim\mathcal{N}(\bm{\mu},\bm{\Sigma})$ in $\mathbb{R}^{D}$ is given by:

h(\bm{x})=\frac{D}{2}(1+\log(2\pi))+\frac{1}{2}\log\det(\bm{\Sigma}).

(3.1.4)

$\blacksquare$

Similar to the entropy for a discrete distribution, we would like the differential entropy to be associated with the coding rate of some realizable coding scheme. For example, as above, we may discretize the domain of the distribution with a grid of size $\epsilon>0$ . The coding rate of the resulting discrete distribution can be viewed as an approximation to the differential entropy [CT91].

Be aware that there are some caveats associated with the definition of differential entropy. For a distribution in a high-dimensional space, when its support becomes degenerate (low-dimensional), its differential entropy diverges to $-\infty$ . This fact is proved in Theorem B.1 (we also recall the maximum entropy characterization of the Gaussian distribution mentioned above in Theorem B.1) but even in the simple explicit case of Gaussian distributions (3.1.4), when the covariance $\bm{\Sigma}$ is singular, we can see that $\log\det(\bm{\Sigma})=-\infty$ so we have $h(\bm{x})=-\infty$ . In such a situation, it is not obvious how to properly quantize or encode such a distribution. Nevertheless, degenerate (Gaussian) distributions are precisely the simplest possible, and arguably the most important, instances of low-dimensional distributions in a high-dimensional space. In this chapter, we will discuss a complete resolution to this seeming difficulty with degeneracy.

3.1.3 Minimizing Coding Rate

Remember that the learning problem entails the recovery of a (potentially continuous) distribution $p(\bm{x})$ from a set of samples $\{\bm{x}_{1},\ldots,\bm{x}_{N}\}$ drawn from the distribution. For ease of exposition, we write $\bm{X}=[\bm{x}_{1},\ldots,\bm{x}_{N}]\in\mathbb{R}^{D\times N}$ . Given that the distributions of interest here are (nearly) low-dimensional, we should expect that their (differential) entropy is very small. But unlike the situations that we have studied in the previous chapter, in general we do not know the family of (analytical) low-dimensional models to which the distribution $p(\bm{x})$ belongs. So checking whether the entropy is small seems to be the only guideline that we can rely on to identify and model the distribution.

Now given the samples alone without knowing what $p(\bm{x})$ is, in theory they could be interpreted as samples from any generic distribution. In particular, they could be interpreted as any of the following cases:

1.

as samples from the empirical distribution $p^{\bm{X}}$ itself, which assigns $1/N$ probability to each of the $N$ samples $\bm{x}_{i},i=1,\ldots,N$ .
2.

as samples from a standard normal distribution $\bm{x}^{n}\sim p^{n}\doteq\mathcal{N}(\bm{0},\sigma^{2}\bm{I})$ with a variance $\sigma^{2}$ large enough (say larger than the sample norms);
3.

as samples from a normal distribution $\bm{x}^{e}\sim p^{e}\doteq\mathcal{N}(\bm{0},\hat{\bm{\Sigma}})$ with a covariance $\hat{\bm{\Sigma}}=\frac{1}{N}\bm{X}\bm{X}^{T}$ being the empirical covariance of the samples;
4.

as samples from a distribution $\hat{\bm{x}}\sim\hat{q}(\bm{x})$ that closely approximates the ground truth distribution $p$ .

Now the question is: which one is better, and in what sense? Suppose that you believe these data $\bm{X}$ are drawn from a particular distribution $q(\bm{x})$ , which may be one of the above distributions considered. Then we could encode the data points with the optimal code book for the distribution $q(\bm{x})$ . The required average coding length (or coding rate) is given by:

\frac{1}{N}\sum_{i=1}^{N}-\log q(\bm{x}_{i})\quad\approx\quad-\int_{\mathbb{R}^{D}}p(\bm{\xi})\log q(\bm{\xi})\mathrm{d}\bm{\xi}

(3.1.5)

as the number of samples $N$ becomes large. If we have identified the correct distribution $p(\bm{x})$ , the coding rate is given by the entropy $-\int p(\bm{\xi})\log p(\bm{\xi})\mathrm{d}\bm{\xi}$ . It turns out that the above coding length $-\int p(\bm{\xi})\log q(\bm{\xi})\mathrm{d}\bm{\xi}$ is always larger than or equal to the entropy unless $q(\bm{x})=p(\bm{x})$ . Their difference, denoted as

	$\displaystyle\operatorname{\mathsf{KL}}(p\;\\|\;q)$	$\displaystyle\doteq$	$\displaystyle-\int_{\mathbb{R}^{D}}p(\bm{\xi})\log q(\bm{\xi})\mathrm{d}\bm{\xi}-\Big{(}-\int_{\mathbb{R}^{D}}p(\bm{\xi})\log p(\bm{\xi})\mathrm{d}\bm{\xi}\Big{)}$		(3.1.6)
		$\displaystyle=$	$\displaystyle\int_{\mathbb{R}^{D}}p(\bm{\xi})\log\frac{p(\bm{\xi})}{q(\bm{\xi})}\mathrm{d}\bm{\xi}$		(3.1.7)

is known as the Kullback-Leibler (KL) divergence, or relative entropy. This quantity is always non-negative.

Theorem 3.1 (Information Inequality).

Let $p(\bm{x}),q(\bm{x})$ be two probability density functions (that have the same support). Then $\operatorname{\mathsf{KL}}(p\;\|\;q)\geq 0$ , where the inequality becomes equality if and only if $p=q$ .⁴⁴4Technically, this equality should be taken to mean “almost everywhere”, i.e., except possibly on a set of zero measure (volume), since this set would not impact the value of any integral.

Proof.

	$\displaystyle-\operatorname{\mathsf{KL}}(p\;\\|\;q)$	$\displaystyle=$	$\displaystyle-\int_{\mathbb{R}^{D}}p(\bm{\xi})\log\frac{p(\bm{\xi})}{q(\bm{\xi})}\mathrm{d}\bm{\xi}=\int_{\mathbb{R}^{D}}p(\bm{\xi})\log\frac{q(\bm{\xi})}{p(\bm{\xi})}\mathrm{d}\bm{\xi}$
		$\displaystyle\leq$	$\displaystyle\log\int_{\mathbb{R}^{D}}p(\bm{\xi})\frac{q(\bm{\xi})}{p(\bm{\xi})}\mathrm{d}\bm{\xi}=\log\int_{\mathbb{R}^{D}}q(\bm{\xi})\mathrm{d}\bm{\xi}=\log 1=0,$

where the first inequality follows from Jensen’s inequality and the fact that the function $\log(\cdot)$ is strictly concave. The equality holds if and only if $p=q$ . ∎

Hence, given a set of sampled data $\bm{X}$ , to determine which case is better among $p^{n}$ , $p^{e}$ , and $\hat{q}$ , we may compare their coding rates for $\bm{X}$ and see which one gives the lowest rate. We know from the above that the (theoretically achievable) coding rate for a distribution is closely related to its entropy. In general, we have:

h(\bm{x}^{n})>h(\bm{x}^{e})>h(\hat{\bm{x}}).

(3.1.8)

Hence, if the data $\bm{X}$ were encoded by the code book associated with each of these distributions, the coding rate for $\bm{X}$ would in general decrease in the same order:

p(\bm{x}^{n})\rightarrow p(\bm{x}^{e})\rightarrow p(\hat{\bm{x}}).

(3.1.9)

This observation gives us a general guideline on how we may be able to pursue a distribution $p(\bm{x})$ which has a low-dimensional structure. It suggests two possible approaches:

1.

Starting with a general distribution (say a normal distribution) with high entropy, gradually transforming the distribution towards the (empirical) distribution of the data by reducing entropy.
2.

Among a large family of (parametric or non-parametric) distributions with explicit coding schemes that encode the given data, progressively search for better coding schemes that give lower coding rates.

Conceptually, both approaches are essentially trying to do the same thing. For the first approach, we need to make sure such a path of transformation exists and is computable. For the second approach, it is necessary that the chosen family is rich enough and can closely approximate (or contain) the ground truth distribution. For either approach, we need to ensure that solutions with lower entropy or better coding rates can be efficiently computed and converge to the desired distribution quickly.⁵⁵5Say the distribution of real-world data such as images and texts. We will explore both approaches in the two remaining sections of this chapter.

3.2 Compression via Denoising

In this section, we will describe a natural and computationally tractable way to learn a distribution $p(\bm{x})$ by way of learning a parametric encoding of our distribution such that the representation has the minimum entropy or coding rate, then using this encoding to transform high-entropy samples from a standard Gaussian into low-entropy samples from the target distribution, as illustrated in Figure 3.2. This presents a methodology that utilizes both approaches above in order to learn and sample from the distribution.

Figure 3.2 : Illustration of an iterative denoising process that, starting from an isotropic Gaussian distribution, converges to an arbitrary data distribution. — Figure 3.2: Illustration of an iterative denoising process that, starting from an isotropic Gaussian distribution, converges to an arbitrary data distribution.

3.2.1 Diffusion and Denoising Processes

We first want to find a procedure to decrease the entropy of a given very noisy sample into a lower-entropy sample from the data distribution. Here, we describe a potential approach—one of many, but perhaps the most natural way to attack this problem. First, we find a way to gradually increase the entropy of existing samples from the data distribution. Then, we find an approximate inverse of this process. But in general, the operation of increasing entropy does not have an inverse, as information from the original distribution may be destroyed. We will thus tackle a special case where (1) the operation of adding entropy takes on a simple, computable, and reversible form; (2) we can obtain a (parametric) encoding of the data distribution, as alluded to in the above pair of approaches. As we will see, the above two factors will ensure that our approach is possible.

We will increase the entropy in arguably the simplest possible way, i.e., adding isotropic Gaussian noise. More precisely, given the random variable $\bm{x}$ , we can consider the stochastic process $(\bm{x}_{t})_{t\in[0,T]}$ which adds gradual noise to it, i.e.,

\bm{x}_{t}\doteq\bm{x}+t\bm{g},\qquad\forall t\in[0,T],

(3.2.1)

where $T\in[0,\infty)$ is a time horizon and $\bm{g}\sim\operatorname{\mathcal{N}}(\bm{0},\bm{I})$ is drawn independently of $\bm{x}$ . This process is an example of a diffusion process, so-named because it spreads the probability mass out over all of $\mathbb{R}^{D}$ as time goes on, increasing the entropy over time. This intuition is confirmed graphically by Figure 3.3, and rigorously via the following theorem.

Theorem 3.2 (Simplified Version of Theorem B.2).

Suppose that $(\bm{x}_{t})_{t\in[0,T]}$ follows the model (3.2.1). For any $t\in(0,T]$ , the random variable $\bm{x}_{t}$ has differential entropy $h(\bm{x}_{t})>-\infty$ . Moreover, under certain technical conditions on $\bm{x}$ ,

\frac{\mathrm{d}}{\mathrm{d}t}h(\bm{x}_{t})>0,\qquad\forall t\in(0,T],

(3.2.2)

showing that the entropy of the noised $\bm{x}$ increases over time $t$ .

The proof is elementary, but it is rather long, so we postpone it to Section B.2.1. The main as-yet unstated implication of this result is that $h(\bm{x}_{t})>h(\bm{x})$ for every $t>0$ . To see this, note that if $h(\bm{x})=-\infty$ then $h(\bm{x}_{t})>-\infty$ for all $t>0$ , and if $h(\bm{x})>-\infty$ then $h(\bm{x}_{t})=h(\bm{x})+\int_{0}^{t}[\frac{\mathrm{d}}{\mathrm{d}s}h(\bm{x}_{s})]\mathrm{d}s>h(\bm{x})$ by the fundamental theorem of calculus, so in both cases $h(\bm{x}_{t})>h(\bm{x})$ for every $t>0$ .

Figure 3.3 : Diffusing a mixture of Gaussians. From left to right, we observe the evolution of the density as t t italic_t grows from 0 to 10 10 10 , along with some representative samples. Each region is colored by its density ( 0.0 0.0 0.0 is completely white, > 0.01 >0.01 > 0.01 is very dark blue, every other value maps to some shade of blue in between.) We observe that the probability mass gets less concentrated as t t italic_t increases, signaling that entropy increases. — Figure 3.3: Diffusing a mixture of Gaussians. From left to right, we observe the evolution of the density as $t$ grows from $0$ to $10$ , along with some representative samples. Each region is colored by its density ( $0.0$ is completely white, $>0.01$ is very dark blue, every other value maps to some shade of blue in between.) We observe that the probability mass gets less concentrated as $t$ increases, signaling that entropy increases.

The inverse operation to adding noise is known as denoising. It is a classical and well-studied topic in signal processing and system theory, such as the Wiener filter and the Kalman filter. Several problems discussed in Chapter 2, such as PCA, ICA, and Dictionary Learning, are specific instances of the denoising problem. For a fixed $t$ and the additive Gaussian noise model (3.2.1), the denoising problem can be formulated as attempting to learn a function $\bar{\bm{x}}^{\ast}(t,\cdot)$ which forms the best possible approximation (in expectation) of the true random variable $\bm{x}$ , given both $t$ and $\bm{x}_{t}$ :

\bar{\bm{x}}^{\ast}(t,\cdot)\in\operatorname*{arg\ min}_{\bar{\bm{x}}(t,\cdot)}\operatorname{\mathbb{E}}_{\bm{x},\bm{x}_{t}}\|\bm{x}-\bar{\bm{x}}(t,\bm{x}_{t})\|_{2}^{2}.

(3.2.3)

The solution to this problem, when optimizing $\bar{\bm{x}}(t,\cdot)$ over all possible (square-integrable) functions, is the so-called Bayes optimal denoiser:

\bar{\bm{x}}^{\ast}(t,\bm{\xi})\doteq\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}].

(3.2.4)

This expression justifies the notation $\bar{\bm{x}}$ , which is meant to compute a conditional expectation (i.e., conditional mean or conditional average). In short, it attempts to remove the noise from the noisy input, outputting the best possible guess (in expectation and w.r.t. the $\ell^{2}$ -distance) of the (de-noised) original random variable.

Example 3.2 (Denoising Gaussian Noise from a Mixture of Gaussians).

In this example we compute the Bayes optimal denoiser for an incredibly important class of distributions, the Gaussian mixture model. To start, let us fix parameters for the distribution: mixture weights $\bm{\pi}\in\mathbb{R}^{K}$ , component means $\{\bm{\mu}_{k}\}_{k=1}^{K}\subseteq\mathbb{R}^{D}$ , and component covariances $\{\bm{\Sigma}_{k}\}_{k=1}^{K}\subseteq\mathsf{PSD}(D)$ , where $\mathsf{PSD}(D)$ is the set of $D\times D$ symmetric positive semidefinite matrices. Now, suppose $\bm{x}$ is generated by the following two-step procedure:

•

First, an index (or label) $y\in[K]$ is sampled such that $y=k$ with probability $\pi_{k}$ .
•

Second, $\bm{x}$ is sampled from the normal distribution $\operatorname{\mathcal{N}}(\bm{\mu}_{y},\bm{\Sigma}_{y})$ .

Then $\bm{x}$ has distribution

\bm{x}\sim\sum_{k=1}^{K}\pi_{k}\operatorname{\mathcal{N}}(\bm{\mu}_{k},\bm{\Sigma}_{k}),

(3.2.5)

and so

\bm{x}_{t}=\bm{x}+t\bm{g}\sim\sum_{k=1}^{K}\pi_{k}\operatorname{\mathcal{N}}(\bm{\mu}_{k},\bm{\Sigma}_{k}+t^{2}\bm{I}).

(3.2.6)

Let us define $\varphi(\bm{x};\bm{\mu},\bm{\Sigma})$ as the probability density of $\operatorname{\mathcal{N}}(\bm{\mu},\bm{\Sigma})$ evaluated at $\bm{x}$ . In this notation, the density of $\bm{x}_{t}$ is

p_{t}(\bm{x}_{t})=\sum_{k=1}^{K}\pi_{k}\varphi(\bm{x}_{t};\bm{\mu}_{k},\bm{\Sigma}_{k}+t^{2}\bm{I}).

(3.2.7)

Conditioned on $y$ , the variables are jointly Gaussian: if we say that $\bm{x}=\bm{\mu}_{y}+\bm{\Sigma}_{y}^{1/2}\bm{u}$ where $(\cdot)^{1/2}$ is the matrix square root and $\bm{u}\sim\operatorname{\mathcal{N}}(\bm{0},\bm{I})$ independently of $y$ (and $\bm{g}$ ), then we have

\begin{bmatrix}\bm{x}\\ \bm{x}_{t}\end{bmatrix}=\begin{bmatrix}\bm{\mu}_{y}\\ \bm{\mu}_{y}\end{bmatrix}+\begin{bmatrix}\bm{\Sigma}_{y}^{1/2}&\bm{0}\\ \bm{\Sigma}_{y}^{1/2}&t\bm{I}\end{bmatrix}\begin{bmatrix}\bm{u}\\ \bm{g}\end{bmatrix}.

(3.2.8)

This shows that $\bm{x}$ and $\bm{x}_{t}$ are jointly Gaussian (conditioned on $y$ ) as claimed. Thus we can write

\begin{bmatrix}\bm{x}\\ \bm{x}_{t}\end{bmatrix}\sim\operatorname{\mathcal{N}}\left(\begin{bmatrix}\bm{\mu}_{y}\\ \bm{\mu}_{y}\end{bmatrix},\begin{bmatrix}\bm{\Sigma}_{y}&\bm{\Sigma}_{y}\\ \bm{\Sigma}_{y}&\bm{\Sigma}_{y}+t^{2}\bm{I}\end{bmatrix}\right).

(3.2.9)

Thus the conditional expectation of $\bm{x}$ given $\bm{x}_{t}$ (i.e., the Bayes optimal denoiser conditioned on $y$ ) is famously (Exercise 3.2)

\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t},y]=\bm{\mu}_{y}+\bm{\Sigma}_{y}(\bm{\Sigma}_{y}+t^{2}\bm{I})^{-1}(\bm{x}_{t}-\bm{\mu}_{y}).

(3.2.10)

To find the overall Bayes optimal denoiser, we use the law of iterated expectation, obtaining

$\displaystyle\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})$	$\displaystyle=\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]$	(3.2.11)
	$\displaystyle=\operatorname{\mathbb{E}}[\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t},y]\mid\bm{x}_{t}]$	(3.2.12)
	$\displaystyle=\sum_{k=1}^{K}\operatorname{\mathbb{P}}[y=k\mid\bm{x}_{t}]\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t},y=k].$	(3.2.13)

The probability can be dealt with as follows. Let $p_{t\mid y}$ be the probability density of $\bm{x}_{t}$ conditioned on the value of $y$ . Then

	$\displaystyle\operatorname{\mathbb{P}}[y=k\mid\bm{x}_{t}]$	$\displaystyle=\frac{p_{t\mid y}(\bm{x}_{t}\mid k)\pi_{k}}{p_{t}(\bm{x}_{t})}$		(3.2.14)
		$\displaystyle=\frac{\pi_{k}\varphi(\bm{x}_{t};\bm{\mu}_{k},\bm{\Sigma}_{k}+t^{2}\bm{I})}{\sum_{i=1}^{K}\pi_{i}\varphi(\bm{x}_{t};\bm{\mu}_{i},\bm{\Sigma}_{i}+t^{2}\bm{I})}.$		(3.2.15)

On the other hand, the conditional expectation is as described before:

\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t},y=k]=\bm{\mu}_{k}+\bm{\Sigma}_{k}(\bm{\Sigma}_{k}+t^{2}\bm{I})^{-1}(\bm{x}_{t}-\bm{\mu}_{k}).

(3.2.16)

So putting this all together, the true Bayes optimal denoiser is

\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})=\sum_{k=1}^{K}\frac{\pi_{k}\varphi(\bm{x}_{t};\bm{\mu}_{k},\bm{\Sigma}_{k}+t^{2}\bm{I})}{\sum_{i=1}^{K}\pi_{i}\varphi(\bm{x}_{t};\bm{\mu}_{i},\bm{\Sigma}_{i}+t^{2}\bm{I})}\cdot\left(\bm{\mu}_{k}+\bm{\Sigma}_{k}(\bm{\Sigma}_{k}+t^{2}\bm{I})^{-1}(\bm{x}_{t}-\bm{\mu}_{k})\right).

(3.2.17)

This example is particularly important, and several special cases will give us great conceptual insight later. For now, let us attempt to extract some geometric intuition from the functional form of the optimal denoiser (3.2.17).

To try to understand (3.2.17) intuitively, let us first set $K=1$ (i.e., one Gaussian) such that $\bm{x}\sim\operatorname{\mathcal{N}}(\bm{\mu},\bm{\Sigma})$ . Let us then diagonalize $\bm{\Sigma}=\bm{V}\bm{\Lambda}\bm{V}^{\top}$ . Then the Bayes optimal denoiser is

\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})=\bm{\mu}+\bm{\Sigma}(\bm{\Sigma}+t^{2}\bm{I})^{-1}(\bm{x}_{t}-\bm{\mu})=\bm{\mu}+\bm{V}\begin{bmatrix}\lambda_{1}/(\lambda_{1}+t^{2})&&\\ &\ddots&\\ &&\lambda_{D}/(\lambda_{D}+t^{2})\end{bmatrix}\bm{V}^{\top}(\bm{x}_{t}-\bm{\mu}),

(3.2.18)

where $\lambda_{1},\dots,\lambda_{D}$ are the eigenvalues of $\bm{\Sigma}$ . We can observe that this denoiser has three steps:

•

Translate the input $\bm{x}_{t}$ by $\bm{\mu}$ .
•

Contract the (translated) input $\bm{x}_{t}-\bm{\mu}$ in each eigenvector direction by a quantity $\lambda_{i}/(\lambda_{i}+t^{2})$ . If the translated input is low-rank and some eigenvalues of $\bm{\Sigma}$ are zero, these directions get immediately contracted to $0$ by the denoiser, ensuring that the output of the contraction is similarly low-rank.
•

Translate the output back by $\bm{\mu}$ .

It is easy to show that it contracts the current $\bm{x}_{t}$ towards the mean $\bm{\mu}$ :

\|\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})-\bm{\mu}\|_{2}\leq\|\bm{x}_{t}-\bm{\mu}\|_{2}.

(3.2.19)

This is the geometric interpretation of the denoiser of a single Gaussian. The overall denoiser of the Gaussian mixture model (3.2.17) uses $K$ such denoisers, weighting their output by the posterior probabilities $\operatorname{\mathbb{P}}[y=k\mid\bm{x}_{t}]$ . If the means of the Gaussians are well-separated, these posterior probabilities are very close to $0$ or $1$ near each mean or cluster. In this regime, the overall denoiser (3.2.17) has the same geometric interpretation as the above single Gaussian denoiser.

At first glance, such a contraction mapping (3.2.19) may appear similar to power iterations (see Section 2.1.2). However, the two are fundamentally different. Power iteration implements a contraction mapping towards a subspace—namely the subspace spanned by the first principal component. In contrast, the iterates in (3.2.19) converge to the mean $\bm{\mu}$ of the underlying distribution, which is a single point. $\blacksquare$

Figure 3.4 : Bayes optimal denoiser and score of a Gaussian mixture model. In the same setting as Figure 3.3 , we demonstrate the effect of the Bayes optimal denoiser 𝒙 ¯ ∗ \bar{\bm{x}}^{\ast} over¯ start_ARG bold_italic_x end_ARG start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT by plotting 𝒙 t \bm{x}_{t} bold_italic_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT (red) and 𝒙 ¯ ∗ ( t , 𝒙 t ) \bar{\bm{x}}^{\ast}(t,\bm{x}_{t}) over¯ start_ARG bold_italic_x end_ARG start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ( italic_t , bold_italic_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT ) (green) for some choice t t italic_t and 𝒙 t \bm{x}_{t} bold_italic_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT . By Tweedie’s formula Theorem 3.3 , the residual between them is proportional to the so-called (Hyvärinen) score ∇ 𝒙 t log ⁡ p t ( 𝒙 t ) \nabla_{\bm{x}_{t}}\log p_{t}(\bm{x}_{t}) ∇ start_POSTSUBSCRIPT bold_italic_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT end_POSTSUBSCRIPT roman_log italic_p start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT ( bold_italic_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT ) . We can see that the score points towards the modes of the distribution of 𝒙 t \bm{x}_{t} bold_italic_x start_POSTSUBSCRIPT italic_t end_POSTSUBSCRIPT . — Figure 3.4: Bayes optimal denoiser and score of a Gaussian mixture model. In the same setting as Figure 3.3, we demonstrate the effect of the Bayes optimal denoiser $\bar{\bm{x}}^{\ast}$ by plotting $\bm{x}_{t}$ (red) and $\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})$ (green) for some choice $t$ and $\bm{x}_{t}$ . By Tweedie’s formula Theorem 3.3, the residual between them is proportional to the so-called (Hyvärinen) score $\nabla_{\bm{x}_{t}}\log p_{t}(\bm{x}_{t})$ . We can see that the score points towards the modes of the distribution of $\bm{x}_{t}$ .

Intuitively, and as we can see from Example 3.2, the Bayes optimal denoiser $\bar{\bm{x}}^{\ast}(t,\cdot)$ should move its input $\bm{x}_{t}$ towards the modes of the distribution of $\bm{x}$ . It turns out that, actually, we can quantify this by showing that the Bayes optimal denoiser takes a gradient ascent step on the (log-)density of $\bm{x}_{t}$ , which (recall) we denoted $p_{t}$ . That is, following the denoiser means moving from the input iterate to a region of higher probability within this (perturbed) distribution. For small $t$ , the perturbation is small so our initial intutition is therefore (almost) exactly right. The picture is visualized in Figure 3.4 and rigorously formulated as Tweedie’s formula [Rob56].

Theorem 3.3 (Tweedie’s Formula).

Suppose that $(\bm{x}_{t})_{t\in[0,T]}$ obeys (3.2.1). Let $p_{t}$ be the density of $\bm{x}_{t}$ (as previously declared). Then

\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]=\bm{x}_{t}+t^{2}\nabla_{\bm{x}_{t}}\log p_{t}(\bm{x}_{t}).

(3.2.20)

Proof.

For the proof let us suppose that $\bm{x}$ has a density (even though the theorem is true without this assumption), and call this density $p$ . Let $p_{0\mid t}$ and $p_{t\mid 0}$ be the conditional densities of $\bm{x}=\bm{x}_{0}$ given $\bm{x}_{t}$ and $\bm{x}_{t}$ given $\bm{x}$ respectively. Let $\varphi(\bm{x};\bm{\mu},\bm{\Sigma})$ be the density of $\operatorname{\mathcal{N}}(\bm{\mu},\bm{\Sigma})$ evaluated at $\bm{x}$ , so that $p_{t\mid 0}(\bm{x}_{t}\mid\bm{x})=\varphi(\bm{x}_{t};\bm{x},t^{2}\bm{I})$ . Then a simple calculation gives

$\displaystyle\nabla_{\bm{x}_{t}}\log p_{t}(\bm{x}_{t})$	$\displaystyle=\frac{\nabla_{\bm{x}_{t}}p_{t}(\bm{x}_{t})}{p_{t}(\bm{x}_{t})}$	(3.2.21)
	$\displaystyle=\frac{1}{p_{t}(\bm{x}_{t})}\nabla_{\bm{x}_{t}}\int_{\mathbb{R}^{D}}p(\bm{x})p_{t\mid 0}(\bm{x}_{t}\mid\bm{x})\mathrm{d}\bm{x}$	(3.2.22)
	$\displaystyle=\frac{1}{p_{t}(\bm{x}_{t})}\nabla_{\bm{x}_{t}}\int_{\mathbb{R}^{D}}p(\bm{x})\varphi(\bm{x}_{t};\bm{x},t^{2}\bm{I})\mathrm{d}\bm{x}$	(3.2.23)
	$\displaystyle=\frac{1}{p_{t}(\bm{x}_{t})}\int_{\mathbb{R}^{D}}p(\bm{x})[\nabla_{\bm{x}_{t}}\varphi(\bm{x}_{t};\bm{x},t^{2}\bm{I})]\mathrm{d}\bm{x}$	(3.2.24)
	$\displaystyle=\frac{1}{p_{t}(\bm{x}_{t})}\int_{\mathbb{R}^{D}}p(\bm{x})\varphi(\bm{x}_{t};\bm{x},t^{2}\bm{I})\left[-\frac{\bm{x}_{t}-\bm{x}}{t^{2}}\right]\mathrm{d}\bm{x}$	(3.2.25)
	$\displaystyle=\frac{1}{t^{2}p_{t}(\bm{x}_{t})}\int_{\mathbb{R}^{D}}p(\bm{x})\varphi(\bm{x}_{t};\bm{x},t^{2}\bm{I})[\bm{x}-\bm{x}_{t}]\mathrm{d}\bm{x}$	(3.2.26)
	$\displaystyle=\frac{1}{t^{2}p_{t}(\bm{x}_{t})}\int_{\mathbb{R}^{D}}p(\bm{x})\varphi(\bm{x}_{t};\bm{x},t^{2}\bm{I})\bm{x}\mathrm{d}\bm{x}-\frac{\bm{x}_{t}}{t^{2}p_{t}(\bm{x}_{t})}\int_{\mathbb{R}^{D}}p(\bm{x})\varphi(\bm{x}_{t};\bm{x},t^{2}\bm{I})\mathrm{d}\bm{x}$	(3.2.27)
	$\displaystyle=\frac{1}{t^{2}p_{t}(\bm{x}_{t})}\int_{\mathbb{R}^{D}}p(\bm{x})p_{t\mid 0}(\bm{x}_{t}\mid\bm{x})\bm{x}\mathrm{d}\bm{x}-\frac{\bm{x}_{t}}{t^{2}p_{t}(\bm{x}_{t})}p_{t}(\bm{x}_{t})$	(3.2.28)
	$\displaystyle=\frac{1}{t^{2}p_{t}(\bm{x}_{t})}\int_{\mathbb{R}^{D}}p_{t}(\bm{x}_{t})p_{0\mid t}(\bm{x}\mid\bm{x}_{t})\bm{x}\mathrm{d}\bm{x}-\frac{\bm{x}_{t}}{t^{2}p_{t}(\bm{x}_{t})}p_{t}(\bm{x}_{t})$	(3.2.29)
	$\displaystyle=\frac{1}{t^{2}}\int_{\mathbb{R}^{D}}p_{0\mid t}(\bm{x}\mid\bm{x}_{t})\bm{x}\mathrm{d}\bm{x}-\frac{\bm{x}_{t}}{t^{2}}$	(3.2.30)
	$\displaystyle=\frac{1}{t^{2}}\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]-\frac{\bm{x}_{t}}{t^{2}}$	(3.2.31)
	$\displaystyle=\frac{\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]-\bm{x}_{t}}{t^{2}}.$	(3.2.32)

Simple rearranging of the above equality proves the theorem. ∎

This result develops a connection between denoising and optimization: the Bayes-optimal denoiser takes a single step of gradient ascent on the perturbed data density $p_{t}$ , and the step size adaptively becomes smaller (i.e., taking more precise steps) as the perturbation to the data distribution grows smaller. The quantity $\nabla_{\bm{x}_{t}}\log p_{t}(\bm{x}_{t})$ is called the (Hyvärinen) score and frequently appears in discussions about denoising, etc.; it first appeared in a paper of Aapo Hyvärinen in the context of ICA [Hyv05].

Similar to how one step of gradient descent is almost never sufficient to minimize an objective in practice when initializing far from the optimum, the output of the Bayes-optimal denoiser $\bar{\bm{x}}^{\ast}(t,\cdot)$ is almost never contained in a high-probability region of the data distribution when $t$ is large, especially when the data have low-dimensional structures. We illustrate this point explicitly in the following example.

Example 3.3 (Denoising a Two-Point Mixture).

Let $x$ be uniform on the two-point set $\{-1,+1\}$ and let $(\bm{x}_{t})_{t\in[0,T]}$ follow (3.2.1). This is precisely a degenerate Gaussian mixture model with priors equal to $\frac{1}{2}$ , means $\{-1,+1\}$ , and covariances both equal to $0$ . For a fixed $t>0$ we can use the calculation of the Bayes-optimal denoiser in (3.2.17) to obtain (proof as exercise)

\bar{x}^{\ast}(t,x_{t})=\frac{\varphi(x_{t};+1,t^{2})-\varphi(x_{t};-1,t^{2})}{\varphi(x_{t};1,t^{2})+\varphi(x_{t};-1,t^{2})}=\tanh\left(-\frac{x_{t}}{t^{2}}\right).

(3.2.33)

For $t$ near $0$ , this quantity is near $\{-1,+1\}$ for almost all inputs $\bar{x}^{\ast}(t,x_{t})$ . However, for $t$ large, this quantity is not necessarily even approximately in the original support of $x$ , which, remember, is $\{-1,+1\}$ . In particular, for $x_{t}\approx 0$ it holds $\bar{x}^{\ast}(t,x_{t})\approx 0$ which lies completely in between the two possible points. Thus $\bar{x}^{\ast}$ will not output “realistic” $x$ . Or more mathematically, the distribution of $\bar{x}(t,x_{t})$ is very different from the distribution of $x$ . $\blacksquare$

Therefore, if we want to denoise the very noisy sample $\bm{x}_{T}$ (where—recall— $T$ is the maximum time), we cannot just use the denoiser once. Instead, we must use the denoiser many times, analogously to gradient descent with decaying step sizes, to converge to a stationary point $\hat{\bm{x}}$ . Namely, we shall use the denoiser to go from $\bm{x}_{T}$ to $\hat{\bm{x}}_{T-\delta}$ which approximates $\bm{x}_{T-\delta}$ , then from $\hat{\bm{x}}_{T-\delta}$ to $\hat{\bm{x}}_{T-2\delta}$ , etc., all the way from $\hat{\bm{x}}_{\delta}$ to $\hat{\bm{x}}=\hat{\bm{x}}_{0}$ . Each time we take a denoising step, the action of the denoiser becomes more like a gradient step on the original (log-)density.

More formally, we uniformly discretize $[0,T]$ into $L+1$ timesteps $0=t_{0}<t_{1}<\cdots<t_{L}=T$ , i.e.,

t_{\ell}=\frac{\ell}{L}T,\qquad\ell\in\{0,1,\dots,L\}.

(3.2.34)

Then for each $\ell\in[L]=\{1,2,\dots,L\}$ , going from $\ell=L$ to $\ell=1$ , we can run the iteration

$\displaystyle\hat{\bm{x}}_{t_{\ell-1}}$	$\displaystyle=\operatorname{\mathbb{E}}[\bm{x}_{t_{\ell-1}}\mid\bm{x}_{t_{\ell}}=\hat{\bm{x}}_{t_{\ell}}]$	(3.2.35)
	$\displaystyle=\operatorname{\mathbb{E}}[\bm{x}+t_{\ell-1}\bm{g}\mid\bm{x}_{t_{\ell}}=\hat{\bm{x}}_{t_{\ell}}]$	(3.2.36)
	$\displaystyle=\operatorname{\mathbb{E}}\left[\bm{x}+t_{\ell-1}\cdot\frac{\bm{x}_{t_{\ell}}-\bm{x}}{t_{\ell}}\mid\bm{x}_{t_{\ell}}=\hat{\bm{x}}_{t_{\ell}}\right]$	(3.2.37)
	$\displaystyle=\frac{t_{\ell-1}}{t_{\ell}}\hat{\bm{x}}_{t_{\ell}}+\left(1-\frac{t_{\ell-1}}{t_{\ell}}\right)\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t_{\ell}}=\hat{\bm{x}}_{t_{\ell}}]$	(3.2.38)
	$\displaystyle=\left(1-\frac{1}{\ell}\right)\cdot\hat{\bm{x}}_{t_{\ell}}+\frac{1}{\ell}\cdot\bar{\bm{x}}^{\ast}(t_{\ell},\hat{\bm{x}}_{t_{\ell}}).$	(3.2.39)

The effect of this iteration is as follows. At the beginning of the iteration, where $\ell$ is large, we barely trust the output of the denoiser and mostly keep the current iterate. This makes sense, as the denoiser can have huge variance (cf Example 3.3). When $\ell$ is small, the denoiser will “lock on” to the modes of the data distribution, as a denoising step basically takes a gradient step on the true distribution’s log-density, and we can trust it not to produce unreasonable samples, so the denoising step mostly involves the output of the denoiser. At $\ell=1$ we even throw away the current iterate and just keep the output of the denoiser.

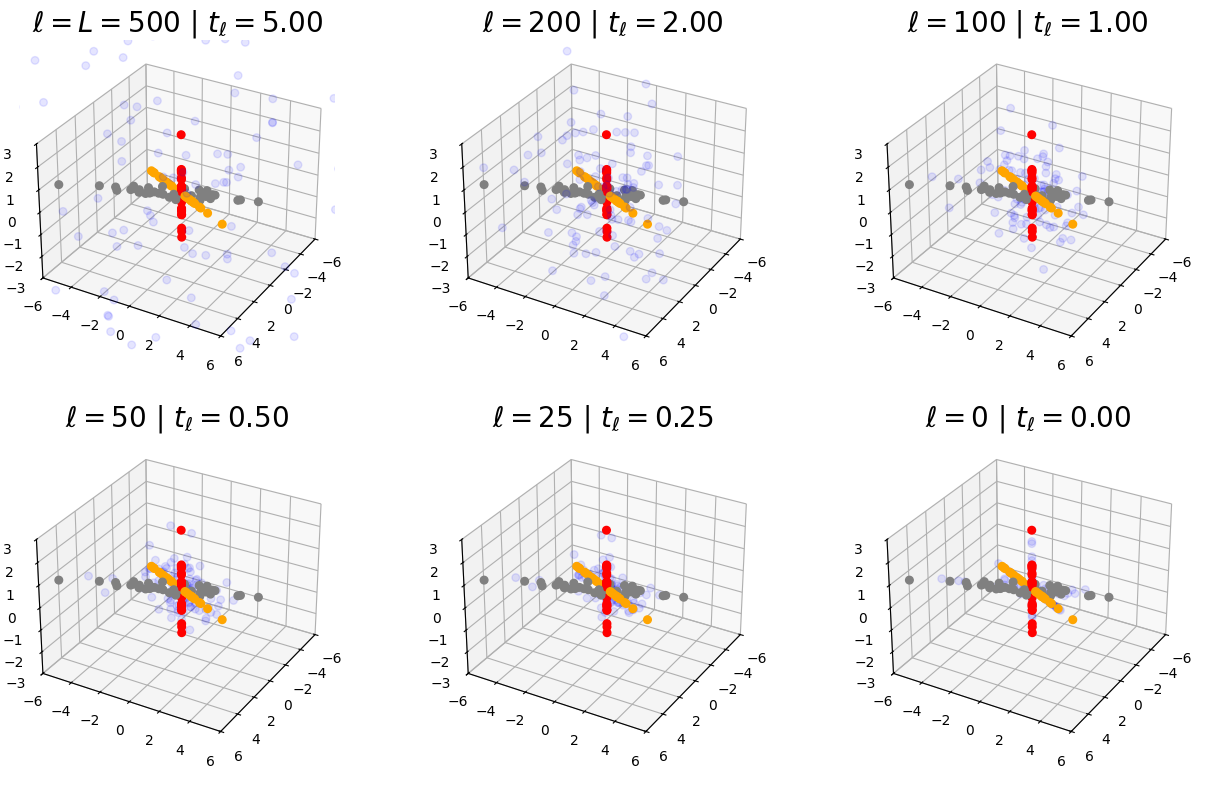
Figure 3.5 : Denoising a low-rank mixture of Gaussians. Each figure represents samples from the true data distribution (gray, orange, red) and samples undergoing the denoising process ( 3.2.66 ) (light blue). At top left, the process has just started, and the noise is very large. As the process continues, the noise is pushed further towards the support of the low-rank data distribution. Finally, in the bottom right, the generated samples are perfectly aligned with the support of the data and look very much like samples drawn from the low-rank Gaussian mixture model. — Figure 3.5: Denoising a low-rank mixture of Gaussians. Each figure represents samples from the true data distribution (gray, orange, red) and samples undergoing the denoising process (3.2.66) (light blue). At top left, the process has just started, and the noise is very large. As the process continues, the noise is pushed further towards the support of the low-rank data distribution. Finally, in the bottom right, the generated samples are perfectly aligned with the support of the data and look very much like samples drawn from the low-rank Gaussian mixture model.

The above is intuition for why we expect the denoising process to converge. We visualize the convergence process in $\mathbb{R}^{3}$ in Figure 3.5. We will develop some rigorous results about convergence later. For now, recall that we wanted to build a process to reduce the entropy. While we did do this in a roundabout way by inverting a process which adds entropy, it is now time to pay the piper and confirm that our iterative denoising process reduces the entropy.

Theorem 3.4 (Simplified Version of Theorem B.3).

Suppose that $(\bm{x}_{t})_{t\in[0,T]}$ obeys (3.2.1). Then, under certain technical conditions on $\bm{x}$ , for every $s<t$ with $s,t\in(0,T]$ ,

h(\operatorname{\mathbb{E}}[\bm{x}_{s}\mid\bm{x}_{t}])<h(\bm{x}_{t}).

(3.2.40)

The full statement of the theorem, and the proof itself, requires some technicality, so it is postponed to Section B.2.2.

The last thing we discuss here is that many times, we will not be able to compute $\bar{\bm{x}}^{\ast}(t,\cdot)$ for any $t$ , since we do not have the distribution $p_{t}$ . But we can try to learn one from data. Recall that the denoiser $\bar{\bm{x}}^{\ast}$ is defined in (3.2.3) as minimizing the mean-squared error $\operatorname{\mathbb{E}}\|\bar{\bm{x}}(t,\bm{x}_{t})-\bm{x}\|_{2}^{2}$ . We can use this mean-squared error as a loss or objective function to learn the denoiser. For example, we can parameterize $\bar{\bm{x}}(t,\cdot)$ by a neural network, writing it as $\bar{\bm{x}}_{\theta}(t,\cdot)$ , and optimize the loss over the parameter space $\Theta$ :

\min_{\theta\in\Theta}\operatorname{\mathbb{E}}_{\bm{x},\bm{x}_{t}}\|\bar{\bm{x}}_{\theta}(t,\bm{x}_{t})-\bm{x}\|_{2}^{2}.

(3.2.41)

The solution to this optimization problem, implemented via gradient descent or a similar algorithm, will give us a $\bar{\bm{x}}_{\theta^{\ast}}(t,\cdot)$ which is a good approximation to $\bar{\bm{x}}^{\ast}(t,\cdot)$ (at least if the training works) and which we will use as our denoiser.

What is a good architecture for this neural network $\bar{\bm{x}}_{\theta^{\ast}}(t,\cdot)$ ? To answer this question, we will examine the ubiquitous case of a Gaussian mixture model, whose denoiser we computed in Example 3.2. This model is relevant because it can approximate many types of distributions: in particular, given a distribution for $\bm{x}$ , there is a Gaussian mixture model that can approximate it arbitrarily well. So optimizing among the class of denoisers for Gaussian mixture models can give us something close to the optimal denoiser for the real data distribution.

In our case, we assume that $\bm{x}$ is low-dimensional, which loosely translates into the requirement that $\bm{x}$ is approximately distributed according to a mixture of low-rank Gaussians. Formally, we write

\bm{x}\sim\frac{1}{K}\sum_{k=1}^{K}\operatorname{\mathcal{N}}(\bm{0},\bm{U}_{k}\bm{U}_{k}^{\top})

(3.2.42)

where $\bm{U}_{k}\in\mathsf{O}(D,P)\subseteq\mathbb{R}^{D\times P}$ is an orthogonal matrix. Then the optimal denoiser under (3.2.1) is (from Example 3.2)

\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})=\sum_{k=1}^{K}\frac{\varphi(\bm{x}_{t};\bm{0},\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})}{\sum_{i=1}^{K}\varphi(\bm{x}_{t};\bm{0},\bm{U}_{i}\bm{U}_{i}^{\top}+t^{2}\bm{I})}\cdot\left(\bm{U}_{k}\bm{U}_{k}^{\top}(\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})^{-1}\bm{x}_{t}\right).

(3.2.43)

Notice that within the computation $\varphi$ and outside of it, we compute the inverse $(\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})^{-1}$ . This is a low-rank perturbation of the full-rank matrix $t^{2}\bm{I}$ , and thus ripe for simplification via the Sherman-Morrison-Woodbury identity, i.e., for matrices $\bm{A},\bm{C},\bm{U},\bm{V}$ such that $\bm{A}$ and $\bm{C}$ are invertible,

(\bm{A}+\bm{U}\bm{C}\bm{V})^{-1}=\bm{A}^{-1}-\bm{A}^{-1}\bm{U}(\bm{C}^{-1}+\bm{V}\bm{A}^{-1}\bm{U})^{-1}\bm{V}\bm{A}^{-1}.

(3.2.44)

We prove this identity in Exercise 3.3. For now we apply this identity with $\bm{A}=t^{2}\bm{I}$ , $\bm{U}=\bm{U}_{k}$ , $\bm{V}=\bm{U}_{k}^{\top}$ , and $\bm{C}=\bm{I}$ , obtaining

$\displaystyle(\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})^{-1}$	$\displaystyle=\frac{1}{t^{2}}\bm{I}-\frac{1}{t^{4}}\bm{U}_{k}\left(\bm{I}+\frac{1}{t^{2}}\bm{U}_{k}^{\top}\bm{U}_{k}\right)^{-1}\bm{U}_{k}^{\top}$	(3.2.45)
	$\displaystyle=\frac{1}{t^{2}}\bm{I}-\frac{1}{t^{4}\left(1+\frac{1}{t^{2}}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}$	(3.2.46)
	$\displaystyle=\frac{1}{t^{2}}\left(\bm{I}-\frac{1}{1+t^{2}}\bm{U}_{k}\bm{U}_{k}^{\top}\right).$	(3.2.47)

Then we can compute the posterior probabilities as follows. Note that since $\bm{U}_{k}$ ’s are all orthogonal, $\det(\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})$ are all the same for each $k$ . So

$\displaystyle\frac{\varphi(\bm{x}_{t};\bm{0},\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})}{\sum_{i=1}^{K}\varphi(\bm{x}_{t};\bm{0},\bm{U}_{i}\bm{U}_{i}^{\top}+t^{2}\bm{I})}$	$\displaystyle=\frac{\exp\left(-\frac{1}{2}\bm{x}_{t}^{\top}(\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})^{-1}\bm{x}_{t}\right)}{\sum_{i=1}^{K}\exp\left(-\frac{1}{2}\bm{x}_{t}^{\top}(\bm{U}_{i}\bm{U}_{i}^{\top}+t^{2}\bm{I})^{-1}\bm{x}_{t}\right)}$	(3.2.48)
	$\displaystyle=\frac{\exp\left(-\frac{1}{2t^{2}}\bm{x}_{t}^{\top}\left(\bm{I}-\frac{1}{1+t^{2}}\bm{U}_{k}\bm{U}_{k}^{\top}\right)\bm{x}_{t}\right)}{\sum_{i=1}^{K}\exp\left(-\frac{1}{2t^{2}}\bm{x}_{t}^{\top}\left(\bm{I}-\frac{1}{1+t^{2}}\bm{U}_{i}\bm{U}_{i}^{\top}\right)\bm{x}_{t}\right)}$	(3.2.49)
	$\displaystyle=\frac{\exp\left(-\frac{1}{2t^{2}}\\|\bm{x}_{t}\\|_{2}^{2}+\frac{1}{2t^{2}(1+t^{2})}\\|\bm{U}_{k}^{\top}\bm{x}_{t}\\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(-\frac{1}{2t^{2}}\\|\bm{x}_{t}\\|_{2}^{2}+\frac{1}{2t^{2}(1+t^{2})}\\|\bm{U}_{i}^{\top}\bm{x}_{t}\\|_{2}^{2}\right)}$	(3.2.50)
	$\displaystyle=\frac{\exp\left(-\frac{1}{2t^{2}}\\|\bm{x}_{t}\\|_{2}^{2}\right)\exp\left(\frac{1}{2t^{2}(1+t^{2})}\\|\bm{U}_{k}^{\top}\bm{x}_{t}\\|_{2}^{2}\right)}{\exp\left(-\frac{1}{2t^{2}}\\|\bm{x}_{t}\\|_{2}^{2}\right)\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\\|\bm{U}_{i}^{\top}\bm{x}_{t}\\|_{2}^{2}\right)}$	(3.2.51)
	$\displaystyle=\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\\|\bm{U}_{k}^{\top}\bm{x}_{t}\\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\\|\bm{U}_{i}^{\top}\bm{x}_{t}\\|_{2}^{2}\right)}.$	(3.2.52)

This is a softmax operation weighted by the projection of $\bm{x}_{t}$ onto each subspace measured by $\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}$ (tempered by a temperature $2t^{2}(1+t^{2})$ ). Meanwhile, the component denoisers can be written as

$\displaystyle\bm{U}_{k}\bm{U}_{k}^{\top}(\bm{U}_{k}\bm{U}_{k}^{\top}+t^{2}\bm{I})^{-1}\bm{x}_{t}$	$\displaystyle=\frac{1}{t^{2}}\bm{U}_{k}\bm{U}_{k}^{\top}\left(\bm{I}-\frac{1}{1+t^{2}}\bm{U}_{k}\bm{U}_{k}^{\top}\right)\bm{x}_{t}$	(3.2.53)
	$\displaystyle=\frac{1}{t^{2}}\left(1-\frac{1}{1+t^{2}}\right)\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t}$	(3.2.54)
	$\displaystyle=\frac{1}{1+t^{2}}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t}.$	(3.2.55)

Putting these together, we have

\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})=\frac{1}{1+t^{2}}\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{k}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t},

(3.2.56)

i.e., a projection of $\bm{x}_{t}$ onto each of $K$ subspaces, weighted by a soft-max operation of a quadratic function of $\bm{x}_{t}$ . This functional form is similar to an attention mechanism in a transformer architecture! As we will see in Chapter 4, this is no coincidence at all; the deep link between denoising and lossy compression (to be covered in Section 3.3) makes transformer denoisers so effective in practice. And so overall, our Gaussian mixture model theory motivates the use of transformer-like neural networks for denoising.

Remark 3.1.

Connections between denoising a distribution and probabilistic PCA. Here, we would like to connect denoising a low-dimensional distribution to probabilistic PCA (see Section 2.1.3 for more details about probabilistic PCA). Suppose that we consider $K=1$ in (3.2.42), i.e., $\bm{x}\sim\operatorname{\mathcal{N}}(\bm{0},\bm{U}\bm{U}^{\top})$ , where $\bm{U}\in\mathsf{O}(D,P)\subseteq\mathbb{R}^{D\times P}$ is an orthogonal matrix. According to (3.2.56), the Bayes optimal denoiser is

\displaystyle\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})=\frac{1}{1+t^{2}}\bm{U}\bm{U}^{\top}\bm{x}_{t}.

(3.2.57)

To learn this Bayes optimal denoiser, we can accordingly parameterize the denoising operator $\bar{\bm{x}}(t,\bm{x}_{t})$ as follows:

\displaystyle\bar{\bm{x}}(t,\bm{x}_{t})=\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}\bm{x}_{t},

(3.2.58)

where $\bm{V}\in\mathsf{O}(D,P)$ are learnable parameters. Substituting this into the training loss (3.2.3) yields

\min_{\bm{V}\in\mathsf{O}(D,P)}\operatorname{\mathbb{E}}_{\bm{x},\bm{x}_{t}}\left\|\bm{x}-\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}\bm{x}_{t}\right\|_{2}^{2}=\operatorname{\mathbb{E}}_{\bm{x},\bm{g}}\left\|\bm{x}-\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}(\bm{x}+t\bm{g})\right\|_{2}^{2},

(3.2.59)

where the equality is due to (3.2.1). Conditioned on $\bm{x}$ , we compute

	$\displaystyle\operatorname{\mathbb{E}}_{\bm{g}}\left\\|\bm{x}-\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}(\bm{x}+t\bm{g})\right\\|_{2}^{2}$	(3.2.60)
$\displaystyle=$	$\displaystyle\left\\|\bm{x}-\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}\bm{x}\right\\|_{2}^{2}-\frac{t}{1+t^{2}}\operatorname{\mathbb{E}}_{\bm{g}}\left\langle\bm{x}-\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}\bm{x},\bm{V}\bm{V}^{\top}\bm{g}\right\rangle+\frac{t^{2}}{(1+t^{2})^{2}}\operatorname{\mathbb{E}}_{\bm{g}}\left\\|\bm{V}\bm{V}^{\top}\bm{g}\right\\|_{2}^{2}$	(3.2.61)
$\displaystyle=$	$\displaystyle\left\\|\bm{x}-\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}\bm{x}\right\\|_{2}^{2}+\frac{t^{2}P}{(1+t^{2})^{2}}$	(3.2.62)

where the second equality follows from $\bm{g}\sim\operatorname{\mathcal{N}}(\bm{0},\bm{I})$ and $\operatorname{\mathbb{E}}_{\bm{g}}\left\|\bm{V}\bm{V}^{\top}\bm{g}\right\|_{2}^{2}=\operatorname{\mathbb{E}}_{\bm{g}}\left\|\bm{V}^{\top}\bm{g}\right\|_{2}^{2}=P$ due to $\bm{V}\in\mathsf{O}(D,P)$ . Therefore, Problem (3.2.59) in equivalent to

\displaystyle\min_{\bm{V}\in\mathsf{O}(D,P)}\operatorname{\mathbb{E}}_{\bm{x}}\left\|\bm{x}-\frac{1}{1+t^{2}}\bm{V}\bm{V}^{\top}\bm{x}\right\|_{2}^{2}=\operatorname{\mathbb{E}}_{\bm{x}}\|\bm{x}\|_{2}^{2}+\left(\frac{1}{(1+t^{2})^{2}}-\frac{2}{1+t^{2}}\right)\operatorname{\mathbb{E}}_{\bm{x}}\|\bm{V}^{\top}\bm{x}\|_{2}^{2}.

(3.2.63)

This is further equivalent to

\displaystyle\max_{\bm{V}\in\mathsf{O}(D,P)}\operatorname{\mathbb{E}}_{\bm{x}}\|\bm{V}^{\top}\bm{x}\|_{2}^{2},

(3.2.64)

which is essentially Problem (2.1.27).

Overall, the learned denoiser forms an (implicit parametric) encoding scheme of the given data, since it can be used to denoise/project onto the data distribution. Training a denoiser is equivalent to finding a better coding scheme, and this partially fulfills one of the desiderata (the second) at the end of Section 3.1.3. In the sequel, we will discuss how to fulfill the other (the first).

3.2.2 Learning and Sampling a Distribution via Iterative Denoising

Remember that at the end of Section 3.1.3, we discussed a pair of desiderata for pursuing a distribution with low-dimensional structure. The first such desideratum is to start with a normal distribution, say with high entropy, and gradually reduce its entropy until it reaches the distribution of the data. We will call this procedure sampling since we are generating new samples. It is now time for us to discuss how to do this with the toolkit we have built up.

We know how to denoise very noisy samples $\bm{x}_{T}$ to attain approximations $\hat{\bm{x}}$ that have similar distributions to the target random variable $\bm{x}$ . But the desideratum says that, to sample, we want to start with a template distribution with no influence from the distribution of $\bm{x}$ and use the denoiser to guide the iterates towards the distribution of $\bm{x}$ . How can we do this? One way is motivated as follows:

\frac{\bm{x}_{T}}{T}=\frac{\bm{x}+T\bm{g}}{T}=\frac{\bm{x}}{T}+\bm{g}\to\bm{g}\sim\operatorname{\mathcal{N}}(\bm{0},\bm{I}).

(3.2.65)

Thus, $\bm{x}_{T}\approx\operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I})$ . This approximation is quite good for almost all practical distributions, and visualized in Figure 3.6.

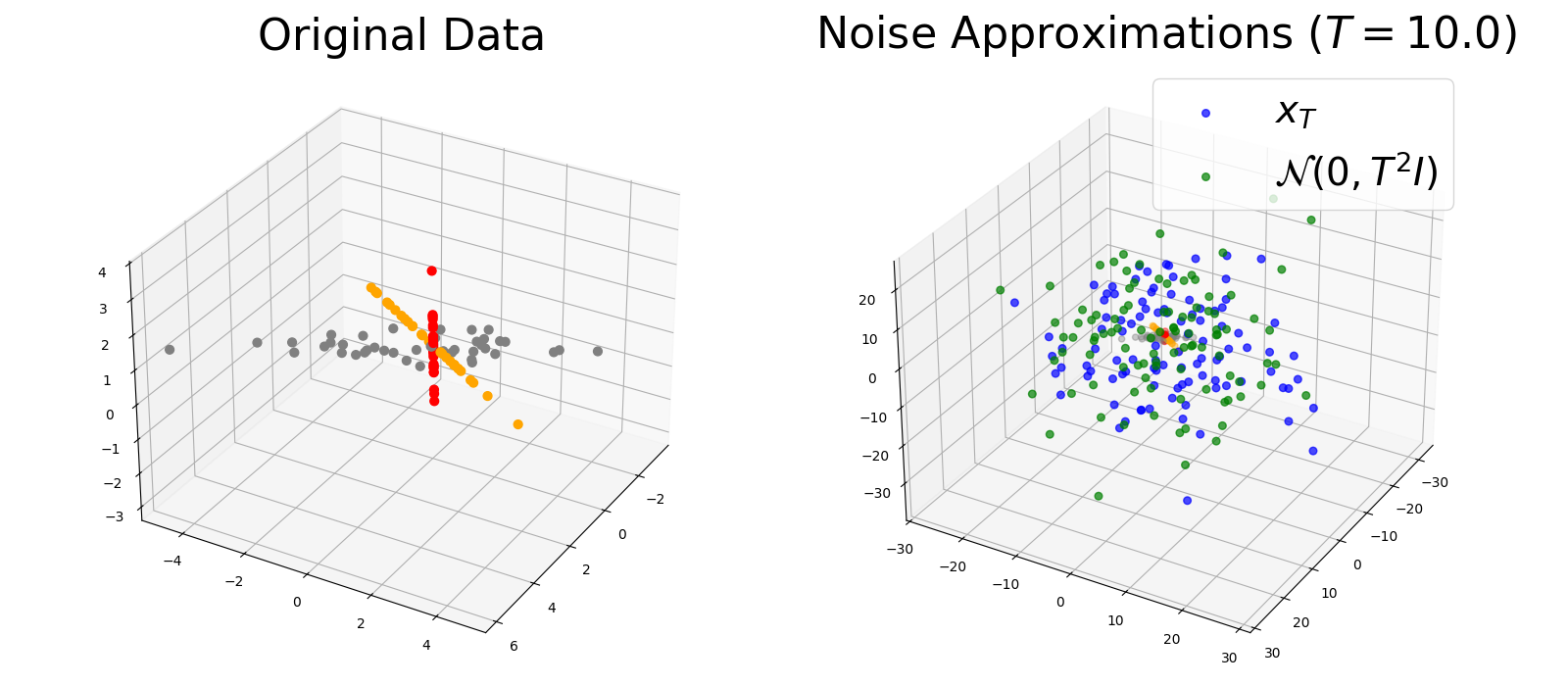
Figure 3.6 : Visualizing x T \bm{x}_{T} bold_italic_x start_POSTSUBSCRIPT italic_T end_POSTSUBSCRIPT versus 𝒩 ⁡ ( 𝟎 , T 2 I ) \operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I}) caligraphic_N ( bold_0 , italic_T start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT bold_italic_I ) . Left: A plot of Gaussian mixture model data 𝒙 \bm{x} bold_italic_x . Right: A plot of 𝒙 \bm{x} bold_italic_x as well as 𝒙 T \bm{x}_{T} bold_italic_x start_POSTSUBSCRIPT italic_T end_POSTSUBSCRIPT and an independent sample of 𝒩 ⁡ ( 𝟎 , T 2 𝑰 ) \operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I}) caligraphic_N ( bold_0 , italic_T start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT bold_italic_I ) , for T = 10 T=10 italic_T = 10 . On the right plot, 𝒙 \bm{x} bold_italic_x is plotted in the same colors as the left: however, samples from 𝒙 T \bm{x}_{T} bold_italic_x start_POSTSUBSCRIPT italic_T end_POSTSUBSCRIPT and 𝒩 ⁡ ( 𝟎 , T 2 𝑰 ) \operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I}) caligraphic_N ( bold_0 , italic_T start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT bold_italic_I ) are both much larger, on average, than samples from 𝒙 \bm{x} bold_italic_x , and so it appears much smaller because of the scaling. Despite this large blow-up, we clearly observe the similarities in the distributions of 𝒙 T \bm{x}_{T} bold_italic_x start_POSTSUBSCRIPT italic_T end_POSTSUBSCRIPT and 𝒩 ⁡ ( 𝟎 , T 2 𝑰 ) \operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I}) caligraphic_N ( bold_0 , italic_T start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT bold_italic_I ) . — Figure 3.6: Visualizing $\bm{x}_{T}$ versus $\operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I})$ . Left: A plot of Gaussian mixture model data $\bm{x}$ . Right: A plot of $\bm{x}$ as well as $\bm{x}_{T}$ and an independent sample of $\operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I})$ , for $T=10$ . On the right plot, $\bm{x}$ is plotted in the same colors as the left: however, samples from $\bm{x}_{T}$ and $\operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I})$ are both much larger, on average, than samples from $\bm{x}$ , and so it appears much smaller because of the scaling. Despite this large blow-up, we clearly observe the similarities in the distributions of $\bm{x}_{T}$ and $\operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I})$ .

So, discretizing $[0,T]$ into $0=t_{0}<t_{1}<\cdots<t_{L}=T$ uniformly using $t_{\ell}=T\ell/L$ (as in the previous section), one possible way to sample from pure noise is:

•

Sample $\hat{\bm{x}}_{T}\sim\operatorname{\mathcal{N}}(\bm{0},T^{2}\bm{I})$ (i.i.d. of everything else)

•

Run the denoising iteration as in Section 3.2.1, i.e.,

\hat{\bm{x}}_{t_{\ell-1}}=\left(1-\frac{1}{\ell}\right)\cdot\hat{\bm{x}}_{t_{\ell}}+\frac{1}{\ell}\cdot\bar{\bm{x}}^{\ast}(t_{\ell},\hat{\bm{x}}_{t_{\ell}}).

(3.2.66)

•

Output $\hat{\bm{x}}=\hat{\bm{x}}_{0}$ .

This conceptually is all there is behind diffusion models, which transform noise into data samples in accordance with the first desideratum. However, there are a few steps left to take before we get models which can actually sample from real data distributions like images given practical resource constraints. In the sequel, we will introduce and motivate several such steps.

Step 1: different discretizations.

The first step we do is motivated by the following point: we do not need to spend so many denoising iterations at large $t$ . If we look at Figure 3.5, we observe that the first $200$ or $300$ iterations out of the $500$ iterations of the sampling process are just spent contracting the noise towards the data distribution as a whole, before the remaining iterations push the samples towards a subspace. Given a fixed iteration count $L$ , this signals that we should spend more timesteps $t_{\ell}$ near $t=0$ compared to $t=T$ . During sampling (and training), we can therefore use another discretization of $[0,T]$ into $0\leq t_{0}<t_{1}<\cdots<t_{L}\leq T$ , such as an exponential discretization:

t_{\ell}=C_{1}(e^{C_{2}\ell}-1),\qquad\forall\ell\in\{0,1,\dots,L\}

(3.2.67)

where $C_{1},C_{2}>0$ are constants which can be tuned for optimal performance in practice; theoretical analysis will often specify such optimal constants as well. Then the denoising/sampling iteration becomes

\hat{\bm{x}}_{t_{\ell-1}}\doteq\frac{t_{\ell-1}}{t_{\ell}}\hat{\bm{x}}_{t_{\ell}}+\left(1-\frac{t_{\ell-1}}{t_{\ell}}\right)\bar{\bm{x}}^{\ast}(t_{\ell},\hat{\bm{x}}_{t_{\ell}}),

(3.2.68)

with, again, $\hat{\bm{x}}_{t_{L}}\sim\operatorname{\mathcal{N}}(\bm{0},t_{L}^{2}\bm{I})$ .

Step 2: different noise models.

The second step is to consider slightly different models compared to (3.2.1). The basic motivation for this is as follows. In practice, the noise distribution $\operatorname{\mathcal{N}}(\bm{0},t_{L}^{2}\bm{I})$ becomes an increasingly poor estimate of the true covariance in high dimensions, i.e., (3.2.65) becomes an increasingly worse approximation, especially with anisotropic high-dimensional data. The increased distance between $\operatorname{\mathcal{N}}(\bm{0},t_{L}^{2}\bm{I})$ and the true distribution of $\bm{x}_{t_{L}}$ may cause the denoiser to perform worse in such circumstances. Theoretically, $\bm{x}_{t_{L}}$ never converges to any distribution as $t_{L}$ increases, so this setup is difficult to analyze end-to-end. In this case, our remedy is to simultaneously add noise and shrink the contribution of $\bm{x}$ , such that $\bm{x}_{T}$ converges as $T\to\infty$ . The rate of added noise is denoted $\sigma\colon[0,T]\to\mathbb{R}_{\geq 0}$ , and the rate of shrinkage is denoted $\alpha\colon[0,T]\to\mathbb{R}_{\geq 0}$ , such that $\sigma$ is increasing and $\alpha$ is (not strictly) decreasing, and

\bm{x}_{t}\doteq\alpha_{t}\bm{x}+\sigma_{t}\bm{g},\qquad\forall t\in[0,T].

(3.2.69)

The previous setup has $\alpha_{t}=1$ and $\sigma_{t}=t$ , and this is called the variance-exploding (VE) process. A popular choice which decreases the contribution of $\bm{x}$ , as we described originally, has $T=1$ (so that $t\in[0,1]$ ), $\alpha_{t}=\sqrt{1-t^{2}}$ and $\sigma_{t}=t$ ; this is the variance-preserving (VP) process. Note that under the VP process, $\bm{x}_{1}\sim\operatorname{\mathcal{N}}(\bm{0},\bm{I})$ exactly, so we can just sample from this standard distribution and iteratively denoise. As a result, the VP process is much easier to analyze theoretically and more stable empirically.⁶⁶6Why use the whole $\alpha,\sigma$ setup? As we will see in Exercise 3.5, it encapsulates and unifies many proposed processes, including the recently popular so-called flow matching process. Despite this, the VE and VP processes are still the most popular empirically and theoretically (so far), and so we will consider them in this Section.

With this more general setup, Tweedie’s formula (3.2.20) becomes

\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]=\frac{1}{\alpha_{t}}\left(\bm{x}_{t}+\sigma_{t}^{2}\nabla\log p_{t}(\bm{x})\right).

(3.2.70)

The denoising iteration (3.2.68) becomes

\hat{\bm{x}}_{t_{\ell-1}}=\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\hat{\bm{x}}_{t_{\ell}}+\left(\alpha_{t_{\ell-1}}-\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\alpha_{t_{\ell}}\right)\bar{\bm{x}}^{\ast}(t_{\ell},\hat{\bm{x}}_{t_{\ell}}).

(3.2.71)

Finally, the Gaussian mixture model denoiser (3.2.17) becomes

\bar{\bm{x}}^{\ast}(t,\bm{x}_{t})=\sum_{k=1}^{K}\frac{\pi_{k}\varphi(\bm{x}_{t};\alpha_{t}\bm{\mu}_{k},\alpha_{t}^{2}\bm{\Sigma}_{k}+\sigma_{t}^{2}\bm{I})}{\sum_{i=1}^{K}\pi_{i}\varphi(\bm{x}_{t};\alpha_{t}\bm{\mu}_{i},\alpha_{t}^{2}\bm{\Sigma}_{i}+\sigma_{t}^{2}\bm{I})}\cdot\left(\bm{\mu}_{k}+\alpha_{t}\bm{\Sigma}_{k}(\alpha_{t}^{2}\bm{\Sigma}_{k}+\sigma_{t}^{2}\bm{I})^{-1}(\bm{x}_{t}-\alpha_{t}\bm{\mu}_{k})\right).

(3.2.72)

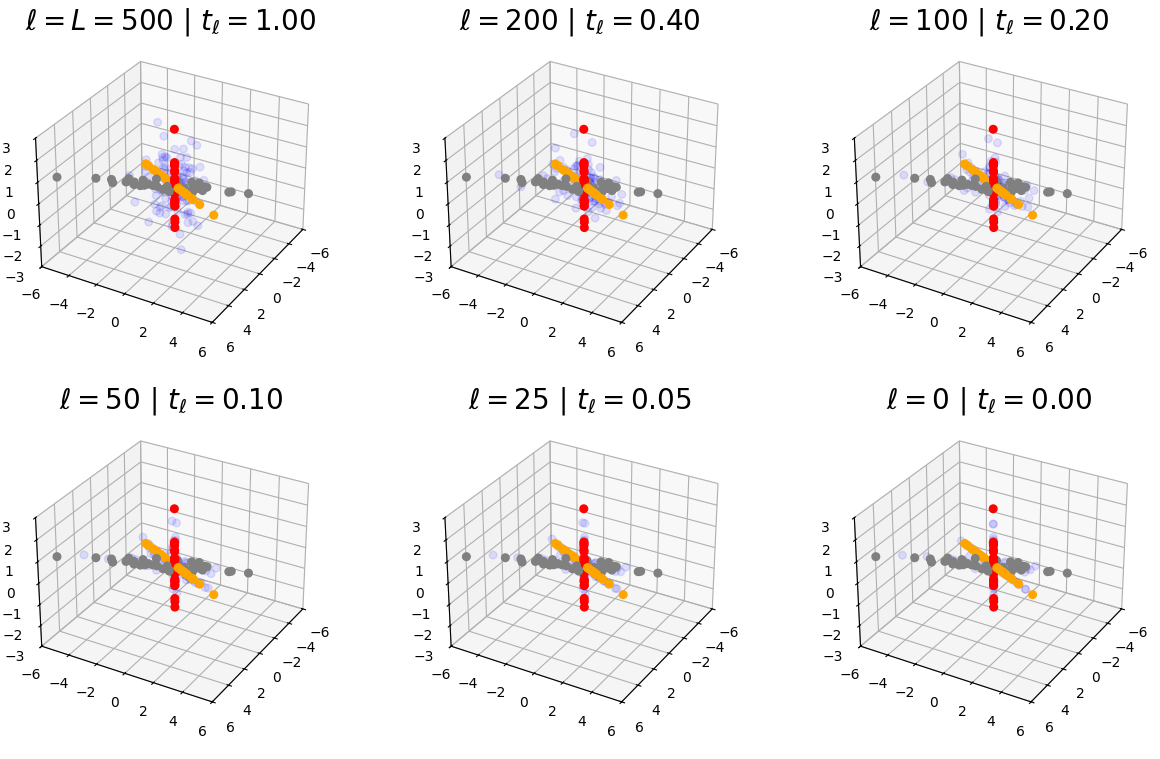
Figure 3.7 demonstrates iterations of the sampling procedure. Note that the denoising iteration (3.2.71) gives a sampling algorithm called the DDIM (“Denoising Diffusion Implicit Model”) sampler [SME20], and is one of the most popular sampling algorithms used today in diffusion models. We summarize it here in Algorithm 3.1.

Figure 3.7 : Denoising a mixture of Gaussians using the VP diffusion process. We use the same figure setup and data distribution as Figure 3.5 . Note that compared to Figure 3.5 , the noise distribution is much more concentrated around the origin. — Figure 3.7: Denoising a mixture of Gaussians using the VP diffusion process. We use the same figure setup and data distribution as Figure 3.5. Note that compared to Figure 3.5, the noise distribution is much more concentrated around the origin.

Algorithm 3.1 Sampling using a denoiser.

1:An ordered list of timesteps

0\leq t_{0}<\cdots<t_{L}\leq T

to use for sampling.

2:A denoiser

\bar{\bm{x}}\colon\{t_{\ell}\}_{\ell=1}^{L}\times\mathbb{R}^{D}\to\mathbb{R}^{D}

3:Scale and noise level functions

\alpha,\sigma\colon\{t_{\ell}\}_{\ell=0}^{L}\to\mathbb{R}_{\geq 0}

4:A sample

\hat{\bm{x}}

, approximately from the distribution of

\bm{x}

5:function DDIMSampler(

\bar{\bm{x}},(t_{\ell})_{\ell=0}^{L}

)

6: Initialize

\tilde{\bm{x}}_{t_{L}}\sim

approximate distribution of

\bm{x}_{t_{L}}

\triangleright

\implies\operatorname{\mathcal{N}}(\bm{0},\bm{I})

, VE

\implies\operatorname{\mathcal{N}}(\bm{0},t_{L}^{2}\bm{I})

7: for

\ell=L,L-1,\dots,1

8: Compute

\hat{\bm{x}}_{t_{\ell-1}}\doteq\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\hat{\bm{x}}_{t_{\ell}}+\left(\alpha_{t_{\ell-1}}-\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\alpha_{t_{\ell}}\right)\bar{\bm{x}}(t_{\ell},\hat{\bm{x}}_{t_{\ell}})

9: end for

10: return

\hat{\bm{x}}_{t_{0}}

11:end function

Step 3: optimizing training pipelines.

If we use the procedure dictated by Section 3.2.1 to learn a separate denoiser $\bar{\bm{x}}(t,\cdot)$ for each time $t$ to be used in the sampling algorithm, we would have to learn $L$ separate denoisers! This is highly inefficient—the usual case is that we have to train $L$ separate neural networks, taking up $L$ times the training time and storage memory, and then be locked into using these timesteps for sampling forever. Instead, we can train a single neural network to denoise across all times $t$ , taking as input the continuous variables $\bm{x}_{t}$ and $t$ (instead of just $\bm{x}_{t}$ before). Mechanically, our training loss averages over $t$ , i.e., solves the following problem:

\min_{\theta}\operatorname{\mathbb{E}}_{t,\bm{x},\bm{x}_{t}}\|\bar{\bm{x}}_{\theta}(t,\bm{x}_{t})-\bm{x}\|_{2}^{2}.

(3.2.73)

Similar to Step 1, where we used more timesteps closer to $t=0$ to ensure a better sampling process, we may want to ensure that the denoiser is higher quality closer to $t=0$ , and thereby weight the loss so that $t$ near $0$ has higher weight. Letting $w_{t}$ be the weight at time $t$ , the weighted loss would look like

\min_{\theta}\operatorname{\mathbb{E}}_{t}w_{t}\operatorname{\mathbb{E}}_{\bm{x},\bm{x}_{t}}\|\bar{\bm{x}}_{\theta}(t,\bm{x}_{t})-\bm{x}\|_{2}^{2}.

(3.2.74)

One reasonable choice of weight in practice is $w_{t}=\alpha_{t}/\sigma_{t}$ . The precise reason will be covered in the next paragraph, but generally it serves to up-weight the losses corresponding to $t$ near $0$ while still remaining reasonably numerically stable. Also, of course, we cannot compute the expectation in practice, so we use the most straightforward Monte-Carlo average to estimate it. The series of changes made here have several conceptual and computational benefits: we do not need to train multiple denoisers, we can train on one set of timesteps and sample using a subset (or others entirely), etc. The full pipeline is discussed in Algorithm 3.2.

1:Dataset

\mathcal{D}\subseteq\mathbb{R}^{D}

2:An ordered list of timesteps

0\leq t_{0}<\cdots<t_{L}\leq T

to use for sampling.

3:A weighting function

w\colon\{t_{\ell}\}_{\ell=1}^{L}\to\mathbb{R}_{\geq 0}

4:Scale and noise level functions

\alpha,\sigma\colon\{t_{\ell}\}_{\ell=0}^{L}\to\mathbb{R}_{\geq 0}

5:A parameter space

\Theta

and a denoiser architecture

\bar{\bm{x}}_{\theta}

6:An optimization algorithm for the parameters.

7:The number of optimization iterations

M

8:The number of Monte-Carlo draws

N

per iteration (to approximate the expectation in (3.2.74))

9:A trained denoiser

\bar{\bm{x}}_{\theta^{\ast}}

10:function TrainDenoiser(

\mathcal{D},\Theta

)

11: Initialize

\theta^{(1)}\in\Theta

12: for

i\in[M]

13: for

n\in[N]

14:

\bm{x}_{n}^{(i)}\sim\mathcal{D}

\triangleright

Draw a sample from the dataset.

15:

t_{n}^{(i)}\stackrel{{\scriptstyle\mathrm{i.i.d.}}}{{\sim}}\operatorname{\mathcal{U}}(\{t_{\ell}\}_{\ell=1}^{L})

\triangleright

Sample a timestep.

16:

\bm{g}_{n}^{(i)}\stackrel{{\scriptstyle\mathrm{i.i.d.}}}{{\sim}}\operatorname{\mathcal{N}}(\bm{0},\bm{I})

\triangleright

Sample a noise vector.

17:

\bm{x}_{t,n}^{(i)}\doteq\alpha_{t_{n}^{(i)}}\bm{x}_{n}^{(i)}+\sigma_{t_{n}^{(i)}}\bm{g}_{n}^{(i)}

\triangleright

Compute the noised sample.

18:

w_{n}^{(i)}\doteq w_{t_{n}^{(i)}}

\triangleright

Compute the loss weight.

19: end for

20:

\hat{\mathcal{L}}^{(i)}\doteq\displaystyle\frac{1}{N}\sum_{n=1}^{N}w_{n}^{(i)}\|\bm{x}_{n}^{(i)}-\bar{\bm{x}}_{\theta^{(i)}}(t_{n}^{(i)},\bm{x}_{t,n}^{(i)})\|_{2}^{2}

\triangleright

Compute the loss estimate.

21:

\theta^{(i+1)}\doteq\texttt{OptimizationUpdate}^{(i)}(\theta^{(i)},\nabla_{\theta^{(i)}}\hat{\mathcal{L}}^{(i)})

\triangleright

Update parameters.

22: end for

23: return

\bar{\bm{x}}_{\theta^{(K+1)}}

24:end function

Algorithm 3.2 Learning a denoiser from data.

(Optional) Step 4: changing the estimation target.

Note that it is common to instead reorient the whole denoising pipeline around noise predictors, i.e., estimates of $\operatorname{\mathbb{E}}[\bm{g}\mid\bm{x}_{t}]$ . In practice, noise predictors are slightly easier to train because their output is (almost) always of comparable size to a Gaussian random variable, so training is more numerically stable. Note that by (3.2.69) we have

\bm{x}_{t}=\alpha_{t}\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]+\sigma_{t}\operatorname{\mathbb{E}}[\bm{g}\mid\bm{x}_{t}]\implies\operatorname{\mathbb{E}}[\bm{g}\mid\bm{x}_{t}]=\frac{1}{\sigma_{t}}\left(\bm{x}_{t}-\alpha_{t}\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]\right),

(3.2.75)

Therefore any predictor for $\bm{x}$ can be turned into a predictor for $\bm{g}$ using the above relation, i.e.,

\bar{\bm{g}}(t,\bm{x}_{t})=\frac{1}{\sigma_{t}}\bm{x}_{t}-\frac{\alpha_{t}}{\sigma_{t}}\bar{\bm{x}}(t,\bm{x}_{t}),

(3.2.76)

and vice-versa. Thus a good network for estimating $\bar{\bm{g}}$ is the same as a good network for estimating $\bar{\bm{x}}$ plus a residual connection (as seen in, e.g., transformers). Their losses are also the same as the denoiser, up to the factor of $\alpha_{t}/\sigma_{t}$ , i.e.,

\operatorname{\mathbb{E}}_{t}w_{t}\operatorname{\mathbb{E}}_{\bm{g},\bm{x}_{t}}\|\bm{g}-\bar{\bm{g}}(t,\bm{x}_{t})\|_{2}^{2}=\operatorname{\mathbb{E}}_{t}w_{t}\frac{\alpha_{t}^{2}}{\sigma_{t}^{2}}\operatorname{\mathbb{E}}_{\bm{x},\bm{x}_{t}}\|\bm{x}-\bar{\bm{x}}(t,\bm{x}_{t})\|_{2}^{2}.

(3.2.77)

For the sake of completeness we will mention that other targets have been proposed for different tasks, e.g., $\operatorname{\mathbb{E}}[\frac{\mathrm{d}}{\mathrm{d}t}\bm{x}_{t}\mid\bm{x}_{t}]$ (called $v$ -prediction or velocity prediction), etc., but denoising and noise prediction remain commonly used. Throughout the rest of this book we will only consider denoising.

We have made lots of changes to our original platonic noising/denoising process. To assure ourselves that the new process still works in practice, we can compute numerical examples (such as Figure 3.7). To assure ourselves that it is theoretically sound, we can prove a bound on the error rate for the sampling algorithm, which shows that the error rate is small. We will now furnish such a rate from the literature, which shows that the output distribution of the sampler converges in the so-called total variation (TV) distance to the true distribution. The TV distance is defined between two random variables $\bm{x}$ and $\bm{y}$ as:

\operatorname{\mathsf{TV}}(\bm{x},\bm{y})\doteq\sup_{A\subseteq\mathbb{R}^{d}}\left\lvert\operatorname{\mathbb{P}}[\bm{x}\in A]-\operatorname{\mathbb{P}}[\bm{y}\in A]\right\rvert.

(3.2.78)

If $\bm{x}$ and $\bm{y}$ are very close (uniformly), then the supremum will be small. So the TV distance measures the closeness of random variables. (It is indeed a metric, as the name suggests; the proof is an exercise.)

Theorem 3.5 ([LY24] Theorem 1, Simplified).

Suppose that $\operatorname{\mathbb{E}}\|\bm{x}\|_{2}<\infty$ . If $\bm{x}$ is denoised according to the VP process with an exponential discretization⁷⁷7The precise definition is rather lengthy in our notation and only defined up to various absolute constants, so we omit it here for brevity. Of course it is in the original paper [LY24]. as in (3.2.67), the output $\hat{\bm{x}}$ of Algorithm 3.1 satisfies the total variation bound

\operatorname{\mathsf{TV}}(\bm{x},\hat{\bm{x}})=\tilde{\mathcal{O}}\left(\underbrace{\frac{D}{L}}_{\text{discretization error}}+\underbrace{\sqrt{\frac{1}{L}\sum_{\ell=1}^{L}\frac{\alpha_{t_{\ell}}}{\sigma_{t_{\ell}}^{2}}\operatorname{\mathbb{E}}_{\bm{x},\bm{x}_{t_{\ell}}}\|\bar{\bm{x}}^{\ast}(t_{\ell},\bm{x}_{t_{\ell}})-\bar{\bm{x}}(t_{\ell},\bm{x}_{t_{\ell}})\|_{2}^{2}}}_{\text{average excess error of the denoiser}}\right)

(3.2.79)

where $\bar{\bm{x}}^{\ast}$ is the Bayes optimal denoiser for $\bm{x}$ , and $\tilde{\mathcal{O}}$ is a version of the big- $\mathcal{O}$ notation which ignores logarithmic factors in $L$ .

The very high-level proof technique is, as discussed earlier, to bound the error at each step, distinguish the error sources (between discretization and denoiser error), and carefully ensure that the errors do not accumulate too much (or even cancel out).

Note that if $L\to\infty$ and we correctly learn the Bayes optimal denoiser $\bar{\bm{x}}=\bar{\bm{x}}^{\ast}$ (such that the excess error is $0$ ), then the sampling process in Algorithm 3.1 yields a perfect (in distribution) inverse of the noising process, since the error rate in Theorem 3.5 goes to $0$ ,⁸⁸8There are similar results for VE processes, though none are as sharp as this to our knowledge. as heuristically argued previously.

Remark 3.2.

What if the data is low-dimensional, say supported on a low-rank subspace of the high dimensional space $\mathbb{R}^{D}$ ? If the data distribution is compactly supported—say if the data is normalized to the unit hypercube, which is often ensured as a pre-processing step for real data such as images—it is possible to do better. Namely, the authors of [LY24] also define a measure of approximate intrinsic dimension using the asymptotics of the so-called covering number, which is extremely similar in intuition (if not in implementation) to the rate distortion function presented in the next Section. Then they show that using a particular small modification of the DDIM sampler in Algorithm 3.1 (i.e., slightly perturbing the update coefficients), the discretization error becomes

\tilde{\mathcal{O}}\left(\frac{\text{approximate intrinsic dimension}}{L}\right)

(3.2.80)

instead of $\frac{D}{L}$ like it was in Theorem 3.5. Therefore, using this modified algorithm, $L$ does not have to be too large even as $D$ reaches the thousands or millions, since real data have low-dimensional structure. However in practice we use the DDIM sampler instead, so $L$ should have a mild dependence on $D$ to achieve consistent error rates. The exact choice of $L$ trades off between the computational complexity (e.g., runtime or memory consumption) of sampling and the statistical complexity of learning a denoiser for low-dimensional structures. The value of $L$ is often different at training time (where a larger $L$ allows better coverage of the interval $[0,T]$ , which helps the network learn a relationship which generalizes over $t$ ) and sampling time (where $L$ being smaller means more efficient sampling). One can even pick the timesteps adaptively at sampling time in order to optimize this tradeoffs [BLZ+22].

Remark 3.3.

Various other works define the reverse process as moving backward in the time index $t$ using an explicit difference equation, or differential equation in the limit $L\to\infty$ , or forward in time using the transformation $\bm{y}_{t}=\bm{x}_{T-t}$ , such that if $t$ increases then $\bm{y}_{t}$ becomes closer to $\bm{x}_{0}$ . In this work we strive to keep consistency: we move forward in time to noise, and backward in time to denoise. If you are reading another work which is not clear on the time index, or trying to implement an algorithm which is similarly unclear, there is one way to do it right every time: the sampling process should always have a positive coefficient on both the denoiser term and the current iterate when moving from step to step. But in general many papers define their own notation and it is not user-friendly.

Remark 3.4.

The theory presented at the end of the last Section 3.2.1 seems to suggest (loosely speaking) that in practice, using a transformer-like network is a good choice for learning or approximating a denoiser. This is reasonable, but what is the problem with using any old neural network (such as a multi-layer perceptron (MLP)) and just trying to scale it up to infinity? To observe the problem with this, let us look at another special case of the Gaussian mixture model studied in Example 3.2. Namely, the empirical distribution is an instance of a degenerate Gaussian mixture model, with $K=N$ components $\operatorname{\mathcal{N}}(\bm{x}_{i},\bm{0})$ sampled with equal probability $\pi_{i}=\frac{1}{N}$ . In this case the Bayes optimal denoiser is

\bar{\bm{x}}^{\star}(t,\bm{x}_{t})=\sum_{i=1}^{N}\frac{e^{-\|\bm{x}_{t}-\alpha_{t}\bm{x}_{i}\|_{2}^{2}/(2\sigma_{t}^{2})}}{\sum_{j=1}^{N}e^{-\|\bm{x}_{t}-\alpha_{t}\bm{x}_{j}\|_{2}^{2}/(2\sigma_{t}^{2})}}\bm{x}_{i}.

(3.2.81)

This is a convex combination of the data $\bm{x}_{i}$ , and the coefficients get “sharper” (i.e., closer to $0$ or $1$ ) as $t\to 0$ . Notice that this denoiser optimally solves the denoising optimization problem (3.2.74) when we compute the loss based on drawing $\bm{x}$ uniformly at random from a fixed finite dataset $\bm{X}=\{\bm{x}_{i}\}_{i=1}^{N}$ , which is a very realistic setting. Thus, if our network architecture $\bar{\bm{x}}_{\theta}$ is expressive enough such that optimal denoisers of the above form (3.2.81) may be well-approximated, then the learned denoiser may do just that. Then, our iterative denoising Algorithm 3.1 will sample exactly from the empirical distribution, re-generating samples in the training data, as certified by Theorem 3.5. This is a bad sampler, not really more interesting than a database of all samples, and so it is important to understand how to avoid this in practice. The key is to come up with a network architecture which can well-approximate the true denoiser (say corresponding to a low-rank distribution as in (3.2.56)) but not the empirical Bayesian denoiser as in (3.2.81). Some work has explored this fine line and why modern diffusion models, which use transformer- and convolutional-based network architectures, can memorize and generalize in different regimes [KG24, NZM+24].

At a high level, a denoiser which memorizes all the training points, as in (3.2.81), corresponds to a parametric model of the distribution which has minimal coding rate, and achieves this by just coding every sample separately. We will discuss this problem (and seeming paradox with our initial desiderata at the end of Section 3.1.3) from the perspective of information theory in the next section.

3.3 Compression via Lossy Coding

Let us recap what we have covered so far. We have discussed how to fit a denoiser $\bar{\bm{x}}_{\theta}$ using finite samples. We showed that this denoiser encodes a distribution in that it is directly connected to its log-density via Tweedie’s formula (3.2.20). Then, we used it to gradually transform a pure noise (high-entropy) distribution towards the learned distribution via iterative denoising. Thus, we have developed the first way of learning or pursuing a distribution laid out at the end of Section 3.1.3.

Nevertheless, in this methodology, the encoding of the distribution is implicit in the denoiser’s functional form and parameters, if any. In fact, acute readers might have noticed that for a general distribution, we have never explicitly specified what the functional form for the denoiser is. In practice, people typically model it by some deep neural network with an empirically designed architecture. In addition, although we know the above denoising process reduces the entropy, we do not know by how much, nor do we know the entropy of the intermediate and resulting distributions.

Recall that our general goal is to model data from a (continuous) distribution with a low-dimensional support. If our goal is to identify the “simplest” model that generates the data, one could consider three typical measures of parsimony: the dimension, the volume, or the (differential) entropy. Well, if one uses the dimension, then obviously the best model for a given dataset is the empirical distribution itself which is zero-dimensional. For all distributions with low-dimensional supports, the differential entropy is always negative infinity; the volume of their supports are always zero. So, among all distributions of low-dimensional supports that could have generated the same data samples, how can we decide which one is better based on these measures of parsimony that cannot distinguish among low-dimensional models at all? This section aims to address this seemingly baffling situation.

In the remainder of this chapter, we discuss a framework that allows us to alleviate the above technical difficulty by associating the learned distribution with an explicit computable encoding and decoding scheme, following the second approach suggested at the end of Section 3.1.3. As we will see, such an approach essentially allows us to accurately approximate the entropy of the learned distributions in terms of a (lossy) coding length or coding rate associated with the coding scheme. With such a measure, not only can we accurately measure how much the entropy is reduced, hence information gained, by any processing (including denoising) of the distribution, but we can also derive an explicit form of the optimal operator that can conduct such operations in the most efficient way. As we will see in the next Chapter 4, this will lead to a principled explanation for the architecture of deep networks, as well as to more efficient deep-architecture designs.

3.3.1 Necessity of Lossy Coding

We have previously, multiple times, discussed a difficulty: if we learn the distribution from finite samples in the end, and our function class of denoisers contains enough functions, how do we ensure that we sample from the true distribution (with low-dimensional supports), instead of any other distribution that may produce those finite samples with high probability? Let us reveal some of the conceptual and technical difficulties with some concrete examples.

Example 3.4 (Volume, Dimension, and Entropy).

For the example shown on the top of Figure 3.8, suppose we have taken some samples from a uniform distribution on a line (say in a 2D plane). The volume of the line or the sample sets is zero. Geometrically, the empirical distribution on the produced finite sample set is the minimum-dimension one which can produce the finite sample set.⁹⁹9A set of discrete samples are all of zero dimension whereas the supporting line is one dimension. But this is in seemingly contrast with yet another measure of complex: entropy. The (differential) entropy of the line is negative infinity but the (discrete) entropy of this sample set is finite and positive. So we seem to have a paradoxical situation according to these common measures of parsimony or complexity: they cannot properly differentiate among (models for) distributions of low-dimensional supports at all, and some seem to differentiate them even in exactly opposite manners.¹⁰¹⁰10Of course, strictly speaking, differential entropy and discrete entropy are not directly comparable. $\blacksquare$

Example 3.5 (Density).

Consider the two sets of sampled data points shown in Figure 3.8. Geometrically, they are essentially the same: each set consists of eight points and each point has occurred with equal frequency $1/8$ th. The only difference is that for the second data set, some points are “close” enough to be viewed as having a higher density around their respective “cluster.” Which one is more relevant to the true distribution that may have generated the samples? How can we reconcile such ambiguity in interpreting this kind of (empirical) distributions?

Figure 3.8 : Eight points observed on a line. — Figure 3.8: Eight points observed on a line.

$\blacksquare$

There is yet another technical difficulty associated with constructing an explicit encoding and decoding scheme for a data set. Given a sampled data set in $\bm{X}=[\bm{x}_{1},\ldots,\bm{x}_{N}]$ , how to design a coding scheme that is implementable on machines with finite memory and computing resources? Note that even representing a general real number requires an infinite number of digits or bits. Therefore, one may wonder whether the entropy of a distribution is a direct measure for the complexity of its (optimal) coding scheme. We examine this matter with another simple example.

Example 3.6 (Precision).

Consider a discrete distribution $\bm{X}=[e,\pi]$ with equal probability $1/2$ taking the values of the Euler number $e\approx 2.71828$ or the number $\pi\approx 3.14159$ . The entropy of this distribution is $H=1$ , which suggests that one may encode the two numbers by a one-bit digit $0$ or $1$ , respectively. But can you realize a decoding scheme for this code on a finite-state machine? The answer is actually no, as it takes infinitely many bits to describe either number precisely. $\blacksquare$

Hence, it is generally impossible to have an encoding and decoding scheme that can precisely reproduce samples from an arbitrary real-valued distribution.¹¹¹¹11That is, if one wants to encode such samples precisely, the only way is to memorize every single sample. But there would be little practical value to encode a distribution without being able to decode for samples drawn from the same distribution.

So to ensure that any encoding/decoding scheme is computable and implementable with finite memory and computational resources, we need to quantify the sample $\bm{x}$ and encode it only up to a certain precision, say $\epsilon>0$ . By doing so, in essence, we treat any two data points equivalent if their distance is less than $\epsilon$ . More precisely, we would like to consider coding schemes

\bm{x}\mapsto\hat{\bm{x}}

(3.3.1)

such that the expected error caused by the quantization is bounded by $\epsilon$ . It is mathematically more convenient, and conceptually almost identical, to bound the expected squared error by $\epsilon^{2}$ , i.e.,

\operatorname{\mathbb{E}}[d(\bm{x},\hat{\bm{x}})^{2}]\leq\epsilon^{2}.

(3.3.2)

Typically, the distance $d$ is chosen to be the Euclidean distance, or the 2-norm.¹²¹²12More generally, we can replace $d^{2}$ with any so-called divergence. We will adopt this choice in the sequel.

3.3.2 Rate Distortion and Data Geometry

Of course, among all encoding schemes that satisfy the above constraint, we would like to choose the one that minimizes the resulting coding rate. For a given random variable $\bm{x}$ and a precision $\epsilon$ , this rate is known as the rate distortion, denoted as $\mathcal{R}_{\epsilon}(\bm{x})$ . A deep theorem in information theory, originally proved by [Sha59], establishes that this rate can be expressed equivalently in purely probabilistic terms as

\mathcal{R}_{\epsilon}(\bm{x})=\min_{p(\hat{\bm{x}}\mid\bm{x}):\operatorname{\mathbb{E}}[\|\bm{x}-\hat{\bm{x}}\|_{2}^{2}]\leq\epsilon^{2}}I(\bm{x};\hat{\bm{x}}),

(3.3.3)

where the quantity $I(\bm{x};\hat{\bm{x}})$ is known as the mutual information, defined by

I(\bm{x};\hat{\bm{x}})=\operatorname{\mathsf{KL}}(p(\bm{x},\hat{\bm{x}})\;\|\;p(\bm{x})p(\hat{\bm{x}})).

(3.3.4)

Note that the minimization in (3.3.3) is over all conditional distributions $p(\hat{\bm{x}}\mid\bm{x})$ that satisfy the distortion constraint $\operatorname{\mathbb{E}}_{\bm{x},\hat{\bm{x}}}[\|\bm{x}-\hat{\bm{x}}\|_{2}^{2}]\leq\epsilon^{2}$ . Each such conditional distribution induces a joint distribution $p(\bm{x},\hat{\bm{x}})=p(\hat{\bm{x}}\mid\bm{x})p(\bm{x})$ , which determines the mutual information (3.3.4). Many convenient properties of the mutual information (and hence the rate distortion) are implied by corresponding properties of the KL divergence (recall Theorem 3.1). From the definition, we know that $\mathcal{R}_{\epsilon}(\bm{x})$ is a non-increasing function in $\epsilon$ .

Remark 3.5.

As it turns out, the rate distortion is an implementable approximation to the entropy of $\bm{x}$ in the following sense. Assume that $\bm{x}$ and $\hat{\bm{x}}$ are continuous random vectors. Then the mutual information can be written as

I(\bm{x};\hat{\bm{x}})=h(\bm{x})-h(\bm{x}\mid\hat{\bm{x}}),

(3.3.5)

where $h(\bm{x}\mid\hat{\bm{x}})=\mathbb{E}[\log_{2}p(\bm{x}\mid\hat{\bm{x}})]$ is the conditional entropy of $\bm{x}$ given $\hat{\bm{x}}$ . Hence, the minimal coding rate is achieved when the difference between the entropy of $\bm{x}$ and the conditional entropy of $\bm{x}$ given $\hat{\bm{x}}$ is minimized among all distributions that satisfy the constraint: $\mathbb{E}[\|\bm{x}-\hat{\bm{x}}\|_{2}^{2}]\leq\epsilon^{2}$ .

In fact, it is not necessary to assume that $\bm{x}$ and $\hat{\bm{x}}$ are continuous to obtain the above type of conclusion. For example, if both random vectors are instead discrete, we have after a suitable interpretation of the KL divergence for discrete-valued random vectors that

I(\bm{x};\hat{\bm{x}})=H(\bm{x})-H(\bm{x}\mid\hat{\bm{x}}).

(3.3.6)

More generally, advanced mathematical notions from measure theory can be used to define the mutual information (and hence the rate distortion) for arbitrary random variables $\bm{x}$ and $\hat{\bm{x}}$ , including those with rather exotic low-dimensional distributions; see [CT91, §8.5].

Remark 3.6.

Given a set of data points in $\bm{X}=[\bm{x}_{1},\ldots,\bm{x}_{N}]$ , one can always interpret them as samples from a uniform discrete distribution with equal probability $1/N$ on these $N$ vectors. The entropy for such a distribution is $H(\bm{X})=\frac{1}{N}\log_{2}N$ .¹³¹³13Note again, even if we can encode these vectors with this coding rate, we cannot decode them with an arbitrary precision. However, even if $\bm{X}$ is a uniform distribution on its samples, the coding rate $\mathcal{R}_{\epsilon}(\bm{X})$ achievable with a lossy coding scheme could be significantly lower than $H(\bm{X})$ if these samples are not so evenly distributed and many are clustered closely to each other. Therefore, for the second distribution shown in Figure 3.8, for a properly chosen quantization error $\epsilon$ , the achievable lossy coding rate can be significantly lower than coding it as a uniform distribution.¹⁴¹⁴14Nevertheless, for this discrete uniform distribution, when $\epsilon$ is small enough, we always have $H(\bm{X})\approx\mathcal{R}_{\epsilon}(\bm{X})$ . Also notice that, with the notion of rate distortion, the difficulty discussed in Example 3.6 also disappears: We can choose two rational numbers that are close enough to each of the two irrational numbers. The resulting coding scheme will have a finite complexity.

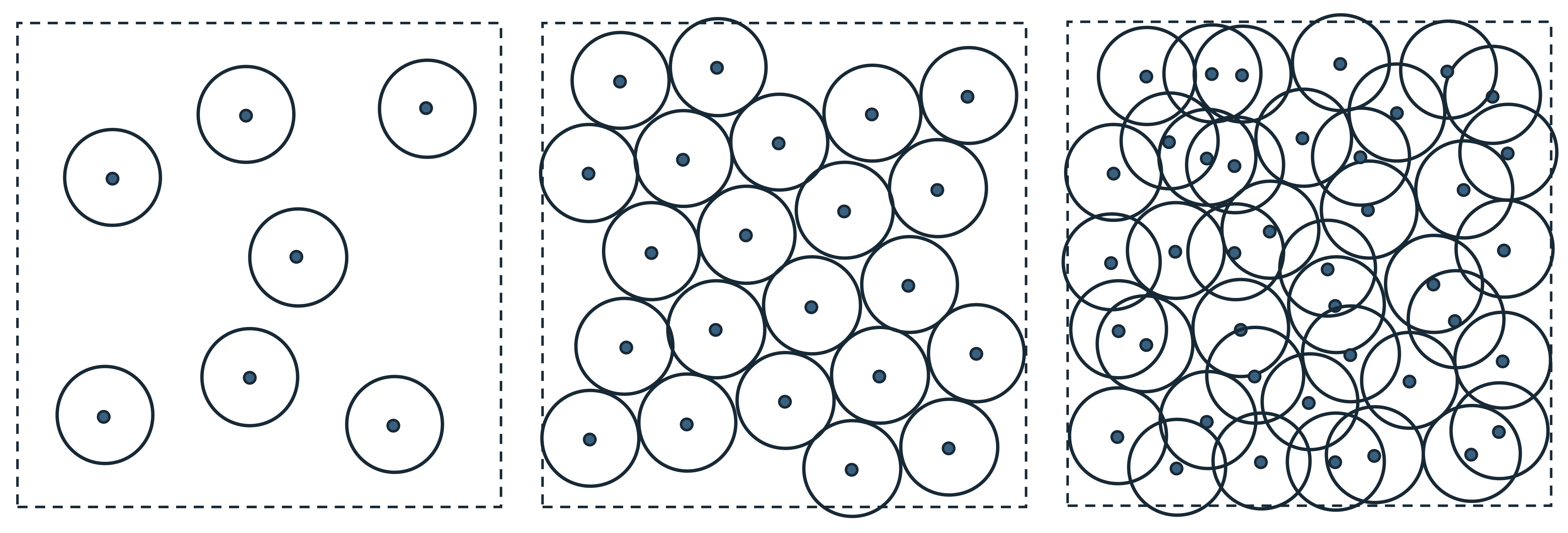
Example 3.7.

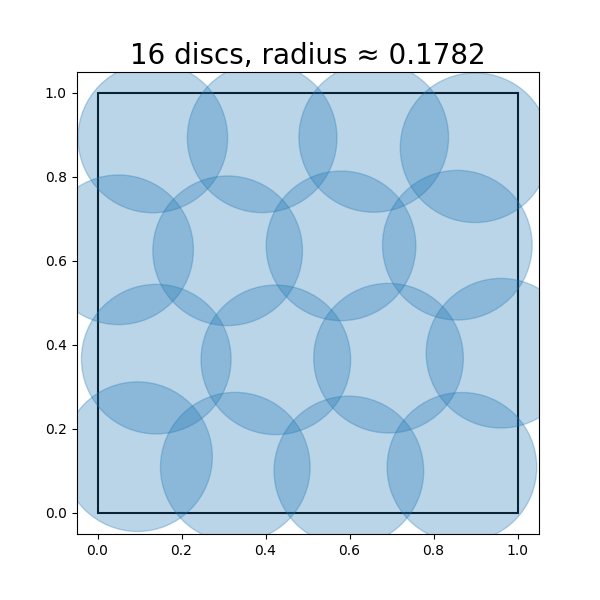
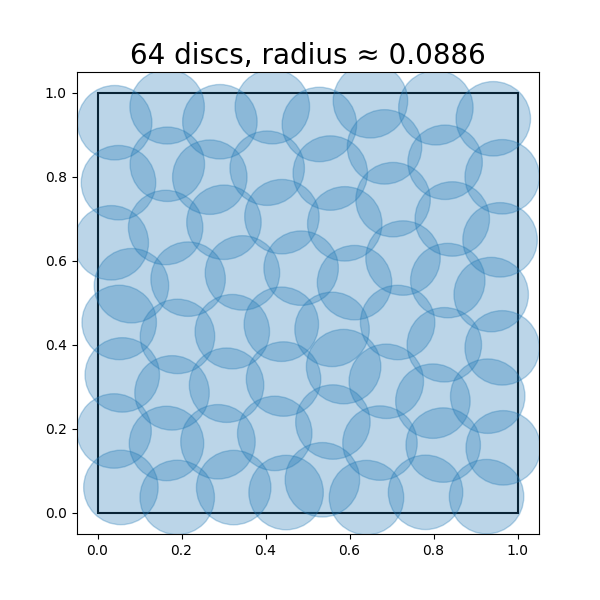
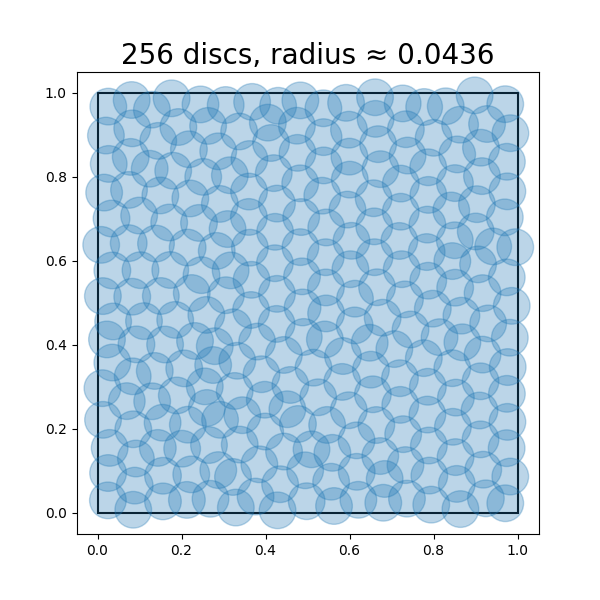
Sometimes, one may face an opposite situation when we want to fix the coding rate first and try to find a coding scheme that minimizes the distortion. For example, suppose that we only want to use a fixed number of codes for points sampled from a distribution, and we want to know how to design the codes such that the average or maximum distortion is minimized during the encoding/decoding scheme. For example, given a uniform distribution on a unit square, we wonder how precisely we can encode points drawn from this distribution, with say $n$ bits. This problem is equivalent to asking what is the minimum radius (i.e., distortion) such that we can cover the unit square with $2^{n}$ discs of this radius. Figure 3.9 shows approximately optimal coverings of a square with $n=4,6,8$ , so that $2^{n}=16,64,256$ discs, respectively. Notice that the optimal radii of the discs decreases as the number of discs $2^{n}$ increases.

Figure 3.9 : Approximations to the optimal solutions for 2 4 2^{4} 2 start_POSTSUPERSCRIPT 4 end_POSTSUPERSCRIPT , 2 6 2^{6} 2 start_POSTSUPERSCRIPT 6 end_POSTSUPERSCRIPT , and 2 8 2^{8} 2 start_POSTSUPERSCRIPT 8 end_POSTSUPERSCRIPT discs covering a square, along with the corresponding radii, calculated using a heuristic optimization algorithm. — Figure 3.9: Approximations to the optimal solutions for $2^{4}$ , $2^{6}$ , and $2^{8}$ discs covering a square, along with the corresponding radii, calculated using a heuristic optimization algorithm.

$\blacksquare$

Figure 3.10 : The approximation of a low-dimensional distribution by ϵ \epsilon italic_ϵ balls. We can see that as the ϵ \epsilon italic_ϵ parameter shrinks, the union of ϵ \epsilon italic_ϵ -balls approximates the support of the true distribution (black) increasingly well. Furthermore, the associated denoisers (whose input-output mapping is given by the provided arrows) obtained by approximating the true distribution by a mixture of Gaussians, each with covariance ( ϵ 2 / D ) 𝑰 (\epsilon^{2}/D)\bm{I} ( italic_ϵ start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT / italic_D ) bold_italic_I , increasingly well-approximate the true denoisers. At large ϵ \epsilon italic_ϵ , such denoisers do not point near the true distribution at all, whereas at small ϵ \epsilon italic_ϵ they closely approximate the true denoisers. Theorem 3.6 establishes that this approximation characterizes the rate distortion function at small distortions ϵ \epsilon italic_ϵ , unifying the parallel approaches of coding rate minimization and denoising for learning low-dimensional distributions without pathologies. — Figure 3.10: The approximation of a low-dimensional distribution by $\epsilon$ balls. We can see that as the $\epsilon$ parameter shrinks, the union of $\epsilon$ -balls approximates the support of the true distribution (black) increasingly well. Furthermore, the associated denoisers (whose input-output mapping is given by the provided arrows) obtained by approximating the true distribution by a mixture of Gaussians, each with covariance $(\epsilon^{2}/D)\bm{I}$ , increasingly well-approximate the true denoisers. At large $\epsilon$ , such denoisers do not point near the true distribution at all, whereas at small $\epsilon$ they closely approximate the true denoisers. Theorem 3.6 establishes that this approximation characterizes the rate distortion function at small distortions $\epsilon$ , unifying the parallel approaches of coding rate minimization and denoising for learning low-dimensional distributions without pathologies.

It turns out to be a notoriously hard problem to obtain closed-form expressions for the rate distortion function (3.3.3) for general distributions $p(\bm{x})$ . However, as Example 3.7 suggests, there are important special cases where the geometry of the support of the distribution $p(\bm{x})$ can be linked to the rate distortion function and hence to the optimal coding rate at distortion level $\epsilon$ . In fact, this example can be generalized to any setting where the support of $p(\bm{x})$ is a sufficiently regular compact set—including low-dimensional distributions—and $p(\bm{x})$ is uniformly distributed on its support. This covers a vast number of cases of practical interest. We formalize this notion in the following result, which establishes this property for a special case.

Theorem 3.6.

Suppose that $\bm{x}$ is a random variable such that its support $K\doteq\operatorname{Supp}(\bm{x})$ is a compact set. Define the covering number $\mathcal{N}_{\epsilon}(K)$ as the minimum number of balls of radius $\epsilon$ that can cover $K$ , i.e.,

\mathcal{N}_{\epsilon}(K)\doteq\min\left\{n\in\mathbb{N}\colon\exists\bm{p}_{1},\dots,\bm{p}_{n}\in K\ \text{s.t.}\ K\subseteq\bigcup_{i=1}^{n}B_{\epsilon}(\bm{p}_{i})\right\},

(3.3.7)

where $B_{\epsilon}(\bm{p})=\{\bm{\xi}\in\mathbb{R}^{D}\mid\|\bm{\xi}-\bm{p}\|_{2}\leq\epsilon\}$ is the Euclidean ball of radius $\epsilon$ centered at $\bm{p}$ . Then it holds

\mathcal{R}_{\epsilon}(\bm{x})\leq\log_{2}\mathcal{N}_{\epsilon}(K).

(3.3.8)

If, in addition, $\bm{x}$ is uniformly distributed on $K$ and $K$ is a mixture of mutually orthogonal low-rank subspaces,¹⁵¹⁵15In fact, it is possible to treat highly irregular $K$ , such as fractals, with a parallel result, but its statement becomes far more technical: c.f. Riegler et al. [RBK18, RKB23]. We give a simple proof in Section B.3 which shows the result for mixtures of subspaces. then a matching lower bound holds:

\mathcal{R}_{\epsilon}(\bm{x})\geq\log_{2}\mathcal{N}_{\epsilon}(K)-O(D).

(3.3.9)

Proof.

A proof of this theorem is beyond the scope of this book and we defer it to Section B.3. ∎

The implication of Theorem 3.6 can be summarized as follows: for sufficiently accurate coding of the distribution of $\bm{x}$ , the minimum rate distortion coding framework is completely characterized by the sphere packing problem on the support of $\bm{x}$ . The core of the proof of Theorem 3.6 can indeed be generalized to more complex distributions such as sufficiently incoherent mixtures of manifolds, but we leave this for a future study. So the rate distortion can be thought of as a “probability-aware” way to approximate the support of the distribution of $\bm{x}$ by a mixture of many small balls.

We now discuss another connection between this and the denoising-diffusion-entropy complexity hierarchy we discussed earlier in this chapter.

Remark 3.7.

The key ingredient in the proof of the lower bound in Theorem 3.6 is an important result from information theory known as the Shannon lower bound for the rate distortion, named after Claude Shannon, who first derived it in a special case [Sha59]. It asserts the following estimate for the rate distortion function, for any random variable $\bm{x}$ with a density $p(\bm{x})$ and finite expected squared norm [LZ94]:

\mathcal{R}_{\epsilon}(\bm{x})\geq h(\bm{x})-\log_{2}\operatorname{vol}(B_{\epsilon})-C_{D},

(3.3.10)

where $C_{D}>0$ is a constant depending only on $D$ . Moreover, this lower bound is actually sharp as $\epsilon\to 0$ : that is,

\lim_{\epsilon\to 0}\mathcal{R}_{\epsilon}(\bm{x})-\left[h(\bm{x})-\log_{2}\operatorname{vol}(B_{\epsilon})-C_{D}\right]=0.

(3.3.11)

So when the distortion $\epsilon$ is small, we can think solely in terms of the Shannon lower bound, rather than the (generally intractable) optimization problem defining the rate distortion (3.3.3).

The Shannon lower bound is the bridge between the coding rate, entropy minimization/denoising, and geometric sphere packing approaches for learning low-dimensional distributions. Notice that in the special case of a uniform density $p(\bm{x})$ , (3.3.10) becomes

	$\displaystyle\mathcal{R}_{\epsilon}(\bm{x})$	$\displaystyle\geq-\int_{K}\frac{1}{\operatorname{vol}(K)}\log_{2}\frac{1}{\operatorname{vol}(K)}\mathrm{d}\bm{\xi}-\log_{2}\operatorname{vol}(B_{\epsilon})-C_{d}$		(3.3.12)
		$\displaystyle=\log_{2}\operatorname{vol}(K)/\operatorname{vol}(B_{\epsilon})-C_{d}.$		(3.3.13)

The ratio $\operatorname{vol}(K)/\operatorname{vol}(B_{\epsilon})$ approximates the number of $\epsilon$ -balls needed to cover $K$ by a worst-case argument, which is accurate for sufficiently regular sets $K$ when $\epsilon$ is small (see Section B.3 for details). Meanwhile, recall the Gaussian denoising model $\bm{x}_{\epsilon}=\bm{x}+\epsilon\bm{g}$ from earlier in the Chapter, where $\bm{g}\sim\mathcal{N}(\mathbf{0},\bm{I})$ is independent of $\bm{x}$ . Interestingly, the differential entropy of the joint distribution $(\bm{x},\bm{g})$ can be calculated as

	$\displaystyle h(\bm{x},\bm{g})$	$\displaystyle=-\int p(\bm{\xi})p(\bm{\gamma})\log_{2}p(\bm{\xi})p(\bm{\gamma})\mathrm{d}\bm{\xi}\mathrm{d}\bm{\gamma}$		(3.3.14)
		$\displaystyle=h(\bm{x})+h(\epsilon\bm{g}).$		(3.3.15)

We have seen the Gaussian entropy calculated in Equation 3.1.4: when $\epsilon$ is small, it is equal, up to additive constants, to the volumetric quantity $-\log_{2}\operatorname{vol}(B_{\epsilon})$ we have seen in the Shannon lower bound. In certain special cases (e.g., data supported on incoherent low-rank subspaces), when $\epsilon$ is small and the support of $\bm{x}$ is sufficiently regular, the distribution of $\bm{x}_{\epsilon}$ can even be well-approximated locally by the product of the distributions $p(\bm{x})$ and $p(\bm{g})$ , justifying the above computation. Hence the Gaussian denoising process yields yet another interpretation of the Shannon lower bound, as arising from the entropy of a noisy version of $\bm{x}$ , with noise level proportional to the distortion level $\epsilon$ .

Thus, this finite rate distortion approach via sphere covering re-enables or generalizes all previous measures of complexity of the distribution, allowing us to differentiate between and rank different distributions in a unified way. These interrelated viewpoints are visualized in Figure 3.10.

For a general distribution at finite distortion levels, it is typically impossible to find its rate distortion function in an analytical form. One must often resort to numerical computation¹⁶¹⁶16Interested readers may refer to [Bla72] for a classic algorithm that computes the rate distortion function numerically for a discrete distribution.. Nevertheless, as we will see, in our context we often need to know the rate distortion as an explicit function of a set of data points or their representations. This is because we want to use the coding rate as a measure of the goodness of the representations. An explicit analytical form makes it easy to determine how to transform the data distribution to improve the representation. So, we should work with distributions whose rate distortion functions take explicit analytical forms. To this end, we start with the simplest, and also the most important, family of distributions.

3.3.3 Lossy Coding Rate for a Low-Dimensional Gaussian

Now suppose we are given a set of data samples in $\bm{X}=[\bm{x}_{1},\ldots,\bm{x}_{N}]$ from any distribution.¹⁷¹⁷17Or these data points could be viewed as an (empirical) distribution themselves. We would like to come up with a constructive scheme that can encode the data up to certain precision, say

\bm{x}_{i}\mapsto\hat{\bm{x}}_{i},\quad\mbox{subject to}\quad\|\bm{x}_{i}-\hat{\bm{x}}_{i}\|_{2}\leq\epsilon.

(3.3.16)

Notice that this is a sufficient, explicit, and interpretable condition which ensures that the data are encoded such that $\frac{1}{N}\sum_{i=1}^{N}\|\bm{x}_{i}-\hat{\bm{x}}_{i}\|_{2}^{2}\leq\epsilon^{2}$ . This latter inequality is exactly the rate distortion constraint for the provided empirical distribution and its encoding. For example, in Example 3.7, we used this simplified criterion to explicitly find the minimum distortion and explicit coding scheme for a given coding rate.

Without loss of generality, let us assume the mean of $\bm{X}$ is zero, i.e., $\frac{1}{N}\sum_{i=1}^{N}\bm{x}_{i}=\bm{0}$ . Without any prior knowledge about the nature of the distribution behind $\bm{X}$ , we may view $\bm{X}$ as sampled from a Gaussian distribution $\mathcal{N}(\bm{0},{\bm{\Sigma}})$ with the covariance¹⁸¹⁸18It is known that given a fixed variance, the Gaussian achieves the maximal entropy. That is, it gives an upper bound for what the worst case could be in terms of possible coding rate.

{\bm{\Sigma}}=\frac{1}{N}\bm{X}\bm{X}^{\top}.

(3.3.17)

Notice that geometrically ${\bm{\Sigma}}$ characterizes an ellipsoidal region where most of the samples $\bm{x}_{i}$ reside.

We may view $\hat{\bm{X}}=[\hat{\bm{x}}_{1},\ldots,\hat{\bm{x}}_{N}]$ as a noisy version of $\bm{X}=[\bm{x}_{1},\ldots,\bm{x}_{N}]$ :

\hat{\bm{x}}_{i}=\bm{x}_{i}+\bm{w}_{i},

(3.3.18)

where $\bm{w}_{i}$ is a Gaussian noise $\bm{w}_{i}\sim\mathcal{N}(\bm{0},{\epsilon^{2}}\bm{I}/{D})$ independent of $\bm{x}_{i}$ . Then the covariance of $\hat{\bm{x}}_{i}$ is given by

\hat{\bm{\Sigma}}=\mathbb{E}\left[\hat{\bm{x}}_{i}\hat{\bm{x}}_{i}^{\top}\right]=\frac{\epsilon^{2}}{D}\bm{I}+\frac{1}{N}\bm{X}\bm{X}^{\top}.

(3.3.19)

Note that the volume of the region spanned by the vectors $\bm{x}_{i}$ is proportional to the square root of the determinant of the covariance matrix

\mbox{volume}(\hat{\bm{x}}_{i})\propto\sqrt{\det\big{(}\hat{\bm{\Sigma}}\big{)}}=\sqrt{\det\left(\frac{\epsilon^{2}}{D}\bm{I}+\frac{1}{N}\bm{X}\bm{X}^{\top}\right)}.

(3.3.20)

The volume spanned by each random vector $\bm{w}_{i}$ is proportional to

\mbox{volume}(\bm{w}_{i})\propto\sqrt{\det\left(\frac{\epsilon^{2}}{D}\bm{I}\right)}.

(3.3.21)

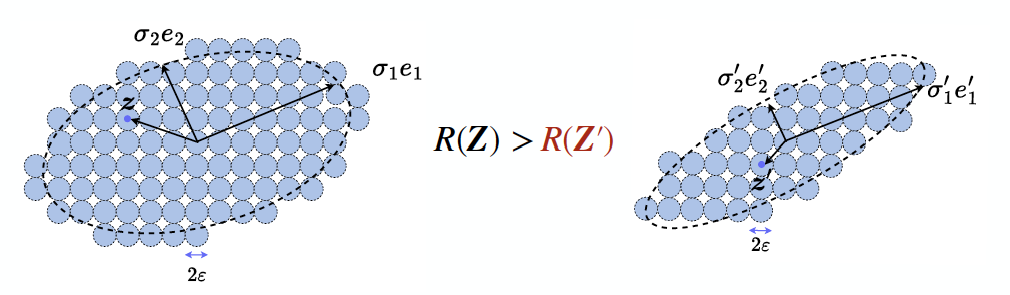
Figure 3.11 : Covering the region spanned by the data vectors using ϵ \epsilon italic_ϵ -balls. The larger the volume of the space, the more balls are needed, hence the more bits are needed to encode and enumerate the balls. Each real-valued vector 𝒙 \bm{x} bold_italic_x can be encoded as the number of the ball which it falls into. — Figure 3.11: Covering the region spanned by the data vectors using $\epsilon$ -balls. The larger the volume of the space, the more balls are needed, hence the more bits are needed to encode and enumerate the balls. Each real-valued vector $\bm{x}$ can be encoded as the number of the ball which it falls into.

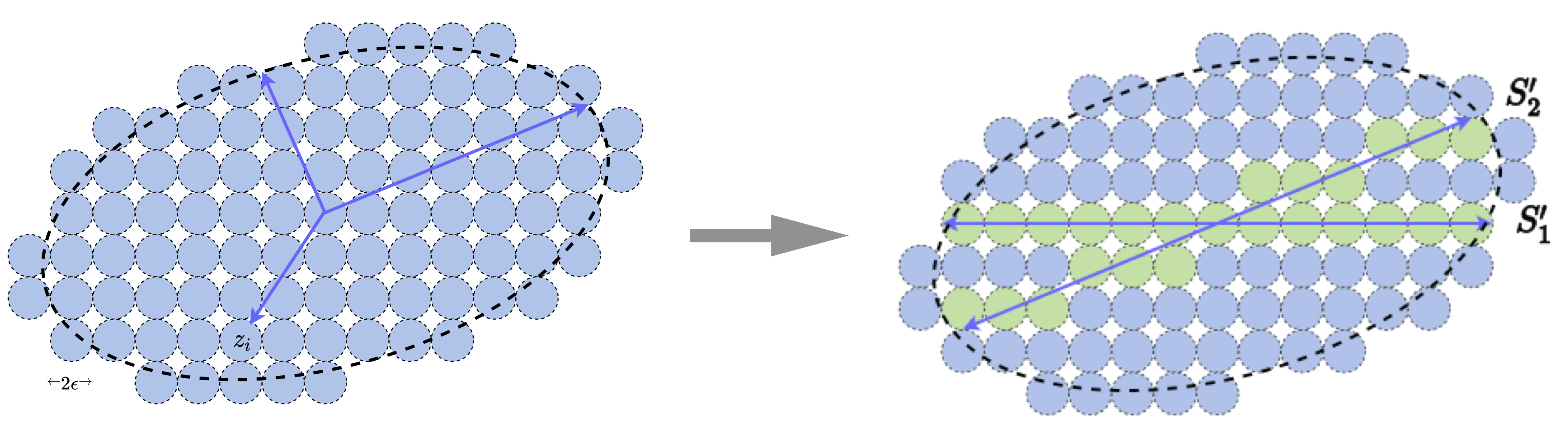
To encode vectors that fall into the region spanned by $\hat{\bm{x}}_{i}$ , we can cover the region with non-overlapping balls of radius $\epsilon$ , as illustrated in Figure 3.11. When the volume of the region spanned by $\hat{\bm{x}}_{i}$ is significantly larger than the volume of the $\epsilon$ -ball, the total number of balls that we need to cover the region is approximately equal to the ratio of the two volumes:

\#\,\epsilon\mbox{-balls}\approx\frac{\mbox{volume}(\hat{\bm{x}}_{i})}{\mbox{volume}(\bm{w}_{i})}=\sqrt{\det\left(\bm{I}+\frac{D}{N\epsilon^{2}}\bm{X}\bm{X}^{\top}\right)}.

(3.3.22)

If we use binary numbers to label all the $\epsilon$ -balls in the region of interest, the total number of binary bits needed is thus

\mathcal{R}_{\epsilon}(\bm{X})\approx\log_{2}(\#\,\epsilon\mbox{-balls})\approx R_{\epsilon}(\bm{X})\doteq\frac{1}{2}\log\det\left(\bm{I}+\frac{D}{N\epsilon^{2}}\bm{X}\bm{X}^{\top}\right).

(3.3.23)

Example 3.8.

Figure 3.11 shows an example of a 2D distribution with an ellipsoidal support – approximating the support of a 2D Gaussian distribution. The region is covered by small balls of size $\epsilon$ . All the balls are numbered from $1$ to say $n$ . Then given any vector $\bm{x}$ in this region, we only need to determine to which $\epsilon$ -ball center it is the closest, denoted as $\operatorname{ball}_{\epsilon}(\bm{x})$ . To remember $\bm{x}$ , we only need to remember the number of this ball, which takes $\log(n)$ bits to store. If we need to decode $\bm{x}$ from this number, we simply take $\hat{\bm{x}}$ as the center of the ball. This leads to an explicit encoding and decoding scheme:

\bm{x}\longrightarrow\operatorname{ball}_{\epsilon}(\bm{x})\longrightarrow\hat{\bm{x}}=\mbox{center of}\operatorname{ball}_{\epsilon}(\bm{x}).

(3.3.24)

One may refer to these ball centers as “codes” of a code book or a dictionary for the encoding scheme. It is easy to see that the accuracy of this (lossy) encoding-decoding scheme is about the radius of the ball $\epsilon$ . Clearly $\mathcal{R}_{\epsilon}(\bm{Z})$ is the average number of bits required to encode the ball number of each vector $\bm{z}$ with this coding scheme, and hence can be called the coding rate associated with this scheme. $\blacksquare$

From the above derivation, we know that the coding rate $\mathcal{R}_{\epsilon}(\bm{X})$ is (approximately) achievable with an explicit encoding (and decoding) scheme. It has two interesting properties:

•

First, one may notice that $R_{\epsilon}(\bm{X})$ closely resembles the rate distortion function of a Gaussian source [CT91]. Indeed, when $\epsilon$ is small, the above expression is a close approximation to the rate distortion of a Gaussian source, as pointed out by [MDH+07].
•

Second, the same closed-form coding rate $R_{\epsilon}(\bm{X})$ can be derived as an approximation of $\mathcal{R}_{\epsilon}(\bm{X})$ if the data $\bm{X}$ are assumed to be from a linear subspace. This can be shown by properly quantifying the singular value decomposition (SVD) of $\bm{X}=\bm{U}\bm{\Sigma}\bm{V}^{\top}$ and constructing a lossy coding scheme for vectors in the subspace spanned by $\bm{U}$ [MDH+07].

In our context, the closed-form expression $R_{\epsilon}(\bm{X})$ is rather fundamental: it is the coding rate associated with an explicit and natural lossy coding scheme for data drawn from either a Gaussian distribution or a linear subspace. As we will see in the next chapter, this formula plays an important role in understanding the architecture of deep neural networks.

3.3.4 Clustering a Mixture of Low-Dimensional Gaussians

As we have discussed before, the given dataset $\bm{X}$ often has low-dimensional intrinsic structures. Hence, encoding it as a general Gaussian would be very redundant. If we can identify those intrinsic structures in $\bm{X}$ , we could design much better coding schemes that give much lower coding rates. Or equivalently, the codes used to encode such $\bm{X}$ can be compressed. We will see that compression gives a unifying computable way to identify such structures. In this section, we demonstrate this important idea with the most basic family of low-dimensional structures: a mixture of (low-dimensional) Gaussians or subspaces.

Example 3.9.

Figure 3.12 shows an example in which the data $\bm{X}$ are distributed around two subspaces (or low-dimensional Gaussians). If they are viewed and coded together as one single Gaussian, the associated discrete (lossy) code book, represented by all the blue balls, is obviously very redundant. We can try to identify the locations of the two subspaces, denoted by $S_{1}$ and $S_{2}$ , and design a code book that only covers the two subspaces, i.e., the green balls. If we can correctly partition samples in the data $\bm{X}$ into the two subspaces: $\bm{X}=[\bm{X}_{1},\bm{X}_{2}]\bm{\Pi}$ with $\bm{X}_{1}\in S_{1}$ and $\bm{X}_{2}\in S_{2}$ , where $\bm{\Pi}$ denotes a permutation matrix, then the resulting coding rate for the data will be much lower. This gives a more parsimonious, hence more desirable, representation of the data. $\blacksquare$

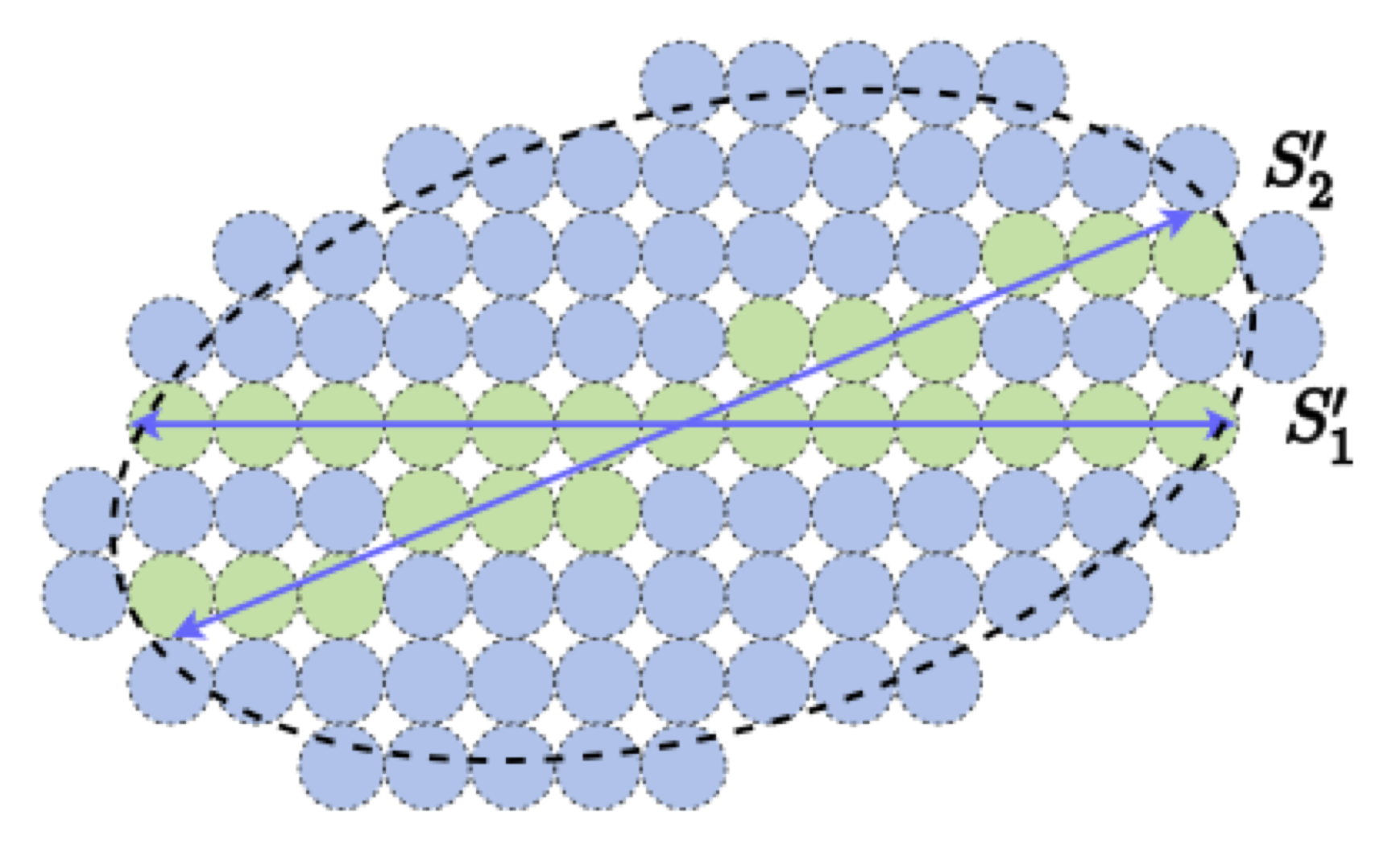
Figure 3.12 : Comparison of two lossy coding schemes for data that are distributed around two subspaces. One is to pack (blue) ϵ \epsilon italic_ϵ -balls for the entire space spanned by the two subspaces; the other is to pack balls only in a tabular neighborhood around the two subspaces. The latter obviously has a much smaller code book and results in a much lower coding rate for samples on the subspaces. — Figure 3.12: Comparison of two lossy coding schemes for data that are distributed around two subspaces. One is to pack (blue) $\epsilon$ -balls for the entire space spanned by the two subspaces; the other is to pack balls only in a tabular neighborhood around the two subspaces. The latter obviously has a much smaller code book and results in a much lower coding rate for samples on the subspaces.

So, more generally speaking, if the data are drawn from any mixture of subspaces or low-dimensional Gaussians, it would be desirable to identify those components and encode the data based on the intrinsic dimensions of those components. It turns out that we do not lose much generality by assuming that the data are drawn from a mixture of low-dimensional Gaussians. This is because a mixture of Gaussians can closely approximate most general distributions [BDS16].

The clustering problem.

Now for this specific family of distributions, how can we effectively and efficiently identify those low-dimensional components from a set of samples

\bm{X}=\left[\bm{x}_{1},\bm{x}_{2},\ldots,\bm{x}_{N}\right],

(3.3.25)

drawn from them? In other words, given the whole data set $\bm{X}$ , we want to partition, or cluster, it into multiple, say $K$ , subsets:

\bm{X}\bm{\Pi}=[\bm{X}_{1},\bm{X}_{2},\dots,\bm{X}_{K}],

(3.3.26)

where each subset consists of samples drawn from only one low-dimensional Gaussian or subspace and $\bm{\Pi}$ is a permutation matrix to indicate membership of the partition. Note that, depending the situation, the partition could be either deterministic or probabilistic. As shown in [MDH+07a], for mixture of Gaussians, probabilistic partition does not lead to a lower coding rate. So for simplicity, we here consider a deterministic partition only.

Clustering via lossy compression.

The main difficulty in solving the above clustering problem is that we normally do not know the number of clusters $K$ , nor do we know the dimension of each component. There has been a long history for the study of this clustering problem. The textbook [VMS16] gives a systematic and comprehensive coverage of different approaches to this problem. To find an effective approach to this problem, we first need to understand and clarify why we want to cluster. In other words, what exactly do we gain from clustering the data, compared with not to? How do we measure the gain? From the perspective of data compression, a correct clustering should lead to a more efficient encoding (and decoding) scheme.

For any given data set $\bm{X}$ , there are already two obvious encoding schemes as the baseline. They represent two extreme ways to encode the data:

•

Simply view all the samples together drawn as from one single Gaussian. The associated coding rate is, as derived before, given by:

\mathcal{R}_{\epsilon}(\bm{X})\approx R_{\epsilon}(\bm{X})=\frac{1}{2}\log\det\left(\bm{I}+\frac{D}{N\epsilon^{2}}\bm{X}\bm{X}^{\top}\right).

(3.3.27)

•

Simply memorize all the samples separately by assigning a different number to each sample. The coding rate would be:

$\mathcal{R}_{0}(\bm{X})=\log(N).$ (3.3.28)

Note that either coding scheme can become the “optimal” solution for certain (extreme) choice of the quantization error $\epsilon$ :

1.

Lazy Regime: If we choose $\epsilon$ to be extremely large, all samples in $\bm{X}$ can be covered by a single ball. The rate is $\lim_{\epsilon\rightarrow\infty}\mathcal{R}_{\epsilon}\rightarrow\frac{1}{2}\log\det(\bm{I})=0$ .
2.

Memorization Regime: If $\epsilon$ is extremely small, every sample in $\bm{X}$ is covered by a different $\epsilon$ -ball, hence the total is $N$ . The rate is $\lim_{\epsilon\rightarrow 0}\mathcal{R}_{\epsilon}\rightarrow\log(N)$ .

Note that the first scheme corresponds to the scenario when one does not care about anything interesting about the distribution at all. One does not want to spare any bit for anything informative. We call this the “lazy regime.” The second scheme corresponds to the scenario when one wants to decode every sample with an extremely high precision. So one would better “memorize” every sample. We call this the “memorization regime.”

Figure 3.13 : A number of random samples on a 2D plane. Consider an ϵ \epsilon italic_ϵ -disc assigned to each sample with the sample as its center. The density of the samples increases from left to right. — Figure 3.13: A number of random samples on a 2D plane. Consider an $\epsilon$ -disc assigned to each sample with the sample as its center. The density of the samples increases from left to right.

Example 3.10.

To see when the memorization regime is preferred or not, let us consider a number, say $N$ , of samples randomly distributed in a unit area on a 2D plane.¹⁹¹⁹19Say the points are drawn by a Poisson process with density $N$ points per unit area. Imagine we try to design a lossy coding scheme with a fixed quantization error $\epsilon$ . This is equivalent to putting an $\epsilon$ -disc around each sample, as shown in Figure 3.13. When $N$ is small, the chance that all the discs overlap with each other is zero. A codebook of size $N$ is necessary and optimal in this case. When $N$ or the density reaches a certain critical value $N_{c}$ , with high probability all the discs start to overlap and connect into one cluster that covers the whole plane—this phenomenon is known as continuum “percolation” [Gil61, MM12]. When $N$ becomes larger than this value, the discs overlap heavily. The number $N$ of discs becomes very redundant because we only want to encode points on the plane up to the given precision $\epsilon$ . The number of discs needed to cover all the samples is much less than $N$ .²⁰²⁰20In fact, there are efficient algorithms to find such a covering [BBF+01]. $\blacksquare$

Both the lazy and memorization regimes are somewhat trivial and perhaps are of little theoretical or practical interest. Either scheme would be far from optimal when used to encode a large number of samples drawn from a distribution that has a compact and low-dimensional support. The interesting regime exists in between these two.

Example 3.11.

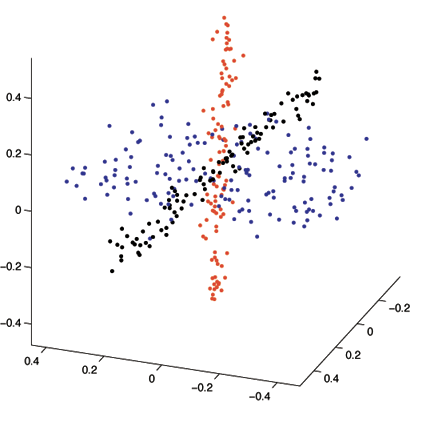
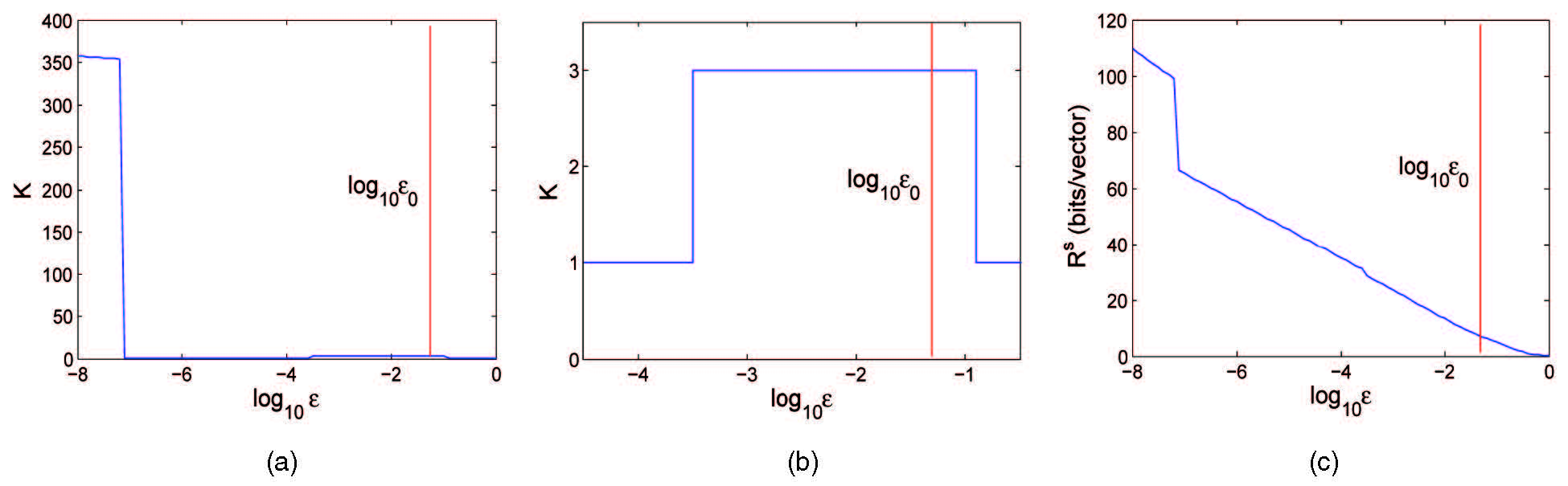
Figure 3.14 : Top: 358 noisy samples drawn from two lines and one plane in ℝ 3 \mathbb{R}^{3} blackboard_R start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT . Bottom: the effect of varying ϵ \epsilon italic_ϵ on the clustering result and the coding rate. The red line marks the variance ϵ 0 \epsilon_{0} italic_ϵ start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT of the Gaussian noise added to the samples. — Figure 3.14: Top: 358 noisy samples drawn from two lines and one plane in $\mathbb{R}^{3}$ . Bottom: the effect of varying $\epsilon$ on the clustering result and the coding rate. The red line marks the variance $\epsilon_{0}$ of the Gaussian noise added to the samples.

Figure 3.14 shows an example with noisy samples drawn from two lines and one plane in $\mathbb{R}^{3}$ . As we notice from the plot (c) on the right, the optimal coding rate decreases monotonically as we increase $\epsilon$ , as anticipated from the property of the rate distortion function. The plots (a) and (b) show, when varying $\epsilon$ from very small (near zero) to very large (towards infinite), the optimal number of clusters when the coding rate is minimal. We can clearly see the lazy regime and the memorization regime on the two ends of the plots. But one can also notice in plot (b), when the quantization error $\epsilon$ is chosen to be around the level of the true noise variance $\epsilon_{0}$ , the optimal number of clusters is the “correct” number three that represents two planes and one subspace. We informally refer to this middle regime as the “generalization regime”. Notice that a sharp phase transition takes place between these regimes.²¹²¹21So far, to our best knowledge, there is no rigorous theoretical justification for these phase transition behaviors. $\blacksquare$

From the above discussion and examples, we see that, when the quantization error relative to the sample density²²²²22or the sample density relative to the quantization error is in a proper range, minimizing the lossy coding rate would allow us to uncover the underlying (low-dimensional) distribution of the sampled data. Hence, quantization, started as a choice of practicality, seems to be becoming necessary for learning a continuous distribution from its empirical distribution with finite samples. Although a rigorous theory for explaining this phenomenon remains elusive, here, for learning purposes, we care about how to exploit the phenomenon to design algorithms that can find the correct distribution.

Let us use the simple example shown in Figure 3.12 to illustrate the basic ideas. If one can partition all samples in $\bm{X}$ into two clusters in $\bm{X}_{1}$ and $\bm{X}_{2}$ , with $N_{1}$ and $N_{2}$ samples respectively, then the associated coding rate would be²³²³23We here ignore some overhead bits needed to encode the membership for each sample, say via the Huffman coding.

R_{\epsilon}^{c}(\bm{X}\mid\bm{\Pi})=\frac{N_{1}}{N}R_{\epsilon}(\bm{X}_{1})+\frac{N_{2}}{N}R_{\epsilon}(\bm{X}_{2}),

(3.3.29)

where we use $\bm{\Pi}$ to indicate membership of the partition. If the partition respects the low-dimensional structures of the distribution, in this case $\bm{X}_{1}$ and $\bm{X}_{2}$ belonging to the two subspaces respectively, then the resulting coding rate should be significantly smaller than the above two basic schemes:

R_{\epsilon}^{c}(\bm{X}\mid\bm{\Pi})\ll R_{\epsilon}(\bm{X}),\quad R_{\epsilon}^{c}(\bm{X}\mid\bm{\Pi})\ll R_{0}(\bm{X}).

(3.3.30)

In general, we can cast the clustering problem into an optimization problem that minimizes the coding rate:

\min_{\bm{\Pi}}\left\{R_{\epsilon}^{c}(\bm{X}\mid\bm{\Pi})\doteq\sum_{k=1}^{K}\frac{N_{k}}{N}R_{\epsilon}(\bm{X}_{k})\right\}.

(3.3.31)

Optimization strategies to cluster.

The remaining question is how we optimize the above coding rate objective to find the optimal clusters. There are three natural approaches to this objective:

1.

We may start with the whole set $\bm{X}$ as a single cluster (i.e. the lazy regime) and then search (say randomly) to partition it so that it would lead to a smaller coding rate.
2.

Inversely, we may start with each sample $\bm{x}_{i}$ as its own cluster (i.e. the memorization regime) and search to merge clusters that would result in a smaller coding rate.
3.

Alternatively, if we could represent (or approximate) the membership $\bm{\Pi}$ as some continuous parameters, we may use optimization methods such as gradient descent (GD).

The first approach is not so appealing computationally as the number of possible partitions that one needs to try is exponential in the number of samples. For example, the number of partitions of $\bm{X}$ into two subsets of equal size is $N\choose N/2$ which explodes as $N$ becomes large. We will explore the third approach in the next Chapter 4. There, we will see how the role of deep neural networks, transformers in particular, is connected with the coding rate objective.

The second approach was originally suggested in the work of [MDH+07a]. It demonstrates the benefit of being able to evaluate the coding rate efficiently (say with an analytical form). With it, the (low-dimensional) clusters of the data can be found rather efficiently and effectively via the principle of minimizing coding length (MCL). Note that for a cluster $\bm{X}_{k}$ with $N_{k}$ samples, the length of binary bits needed to encode all the samples in $\bm{X}_{k}$ is given by:²⁴²⁴24In fact, a more accurate estimate of the coding length is $L(\bm{X}_{k})=(N_{k}+D)R_{\epsilon}(\bm{X}_{k})$ where the extra bits are used to encode the basis of the subspace [MDH+07a]. Here we omit this overhead for simplicity.

L(\bm{X}_{k})=N_{k}R_{\epsilon}(\bm{X}_{k}).

(3.3.32)

If we have two clusters $\bm{X}_{k}$ and $\bm{X}_{l}$ , if we want to code the samples as two separate clusters, the length of binary bits needed is

L^{c}(\bm{X}_{k},\bm{X}_{l})=N_{k}R_{\epsilon}(\bm{X}_{k})+N_{l}R_{\epsilon}(\bm{X}_{l})-N_{k}\log\frac{N_{k}}{N_{k}+N_{l}}-N_{l}\log\frac{N_{l}}{N_{k}+N_{l}}.

The last two terms are the number of bits needed to encode the memberships of samples according to the Huffman code.

Then, given any two separate clusters $\bm{X}_{1}$ and $\bm{X}_{2}$ , we can decide whether to merge them or not based on the difference between the two coding lengths:

L(\bm{X}_{k}\cup\bm{X}_{l})-L^{c}(\bm{X}_{k},\bm{X}_{l})

(3.3.33)

is positive or negative and $\bm{X}_{k}\cup\bm{X}_{l}$ denotes the union of the sets of samples in $\bm{X}_{k}$ and $\bm{X}_{l}$ . If it is negative, it means the coding length would become smaller if we merge the two clusters into one. This simple fact leads to the following clustering algorithm proposed by [MDH+07a]:

Algorithm 3.3 Pairwise Steepest Descent of Coding Length

N

data points

\{\bm{x}_{i}\}_{i=1}^{N}

2:A set

\mathcal{C}

of clusters

3:procedure PairwiseSteepestDescentOfCodingLength(

\{\bm{x}_{i}\}_{i=1}^{N}

)

\mathcal{C}\leftarrow\{\{\bm{x}_{i}\}\}_{i=1}^{N}

\triangleright

Initialize

N

clusters

\bm{X}_{k}

with one element each

5: while

\lvert\mathcal{C}\rvert>1

6: if

\displaystyle\min_{\bm{X}_{k},\bm{X}_{l}\in\mathcal{C}}[L(\bm{X}_{k}\cup\bm{X}_{l})-L^{c}(\bm{X}_{k},\bm{X}_{l})]\geq 0

then

\triangleright

If no bits are saved by any merging

7: return

\mathcal{C}

\triangleright

Early return

\mathcal{C}

and exit

8: else

\displaystyle\bm{X}_{k^{\ast}},\bm{X}_{l^{\ast}}\leftarrow\operatorname*{arg\ min}_{\bm{X}_{k},\bm{X}_{l}\in\mathcal{C}}[L(\bm{X}_{k}\cup\bm{X}_{l})-L^{c}(\bm{X}_{k},\bm{X}_{l})]

\triangleright

Merge clusters which save the most bits

10:

\displaystyle\mathcal{C}\leftarrow[\mathcal{C}\setminus\{\bm{X}_{k^{\ast}},\bm{X}_{l^{\ast}}\}]\cup\{\bm{X}_{k^{\ast}}\cup\bm{X}_{l^{\ast}}\}

\triangleright

Remove unmerged clusters and add back the merged one

11: end if

12: end while

13: return

\mathcal{C}

\triangleright

If all merges yield savings, return one cluster

14:end procedure

Note that this algorithm is tractable as the total number of (pairwise) comparisons and merges is about $O(N^{2}\log N)$ . However, due to its greedy nature, there is no theoretical guarantee that the process will converge to the globally optimal clustering solution. Nevertheless, as reported in [MDH+07a], in practice, this seemingly simple algorithm works extremely well. The clustering results plotted in Figure 3.14 were actually computed by this algorithm.

Example 3.12 (Image Segmentation).

The above measure of coding length and the associated clustering algorithm assume the data distribution is a mixture of (low-dimensional) Gaussians. Although this seems somewhat idealistic, the measure and algorithm can already be very useful and even powerful in scenarios when the model is (approximately) valid.

For example, a natural image typically consists of multiple regions with nearly homogeneous textures. If we take many small windows from each region, they should resemble samples drawn from a (low-dimensional) Gaussian, as illustrated in Figure 3.15. Figure 3.16 shows the results of image segmentation based on applying the above clustering algorithm to the image patches directly. More technical details regarding customizing the algorithm to the image segmentation problem can be found in [MRY+11]. $\blacksquare$

Figure 3.15 : Image patches with a size of w × w w\times w italic_w × italic_w pixels. — Figure 3.15: Image patches with a size of $w\times w$ pixels.

Figure 3.16 : Segmentation results based on the clustering algorithm applied to the image patches. — Figure 3.16: Segmentation results based on the clustering algorithm applied to the image patches.

3.4 Maximizing Information Gain

So far in this chapter, we have discussed how to identify a distribution with low-dimensional structures through the principle of compression. As we have seen from the previous two sections, computational compression can be realized through either the denoising operation or clustering. Figure 3.17 illustrates this concept with our favorite example.

Figure 3.17 : Identify a low-dimensional distribution with two subspaces (left) via denoising or clustering, starting from a generic random Gaussian distribution (right). — Figure 3.17: Identify a low-dimensional distribution with two subspaces (left) via denoising or clustering, starting from a generic random Gaussian distribution (right).

Of course, the ultimate goal for identifying a data distribution is to use it to facilitate certain subsequent tasks such as segmentation, classification, or generation (of images). Hence, how the resulting distribution is “represented” matters tremendously with respect to how information related to these subsequent tasks can be efficiently and effectively retrieved and utilized. This naturally raises a fundamental question: what makes a representation truly “good” for downstream use? In the following, we will explore the essential properties that a meaningful and useful representation should possess, and how these properties can be explicitly characterized and pursued via maximizing information gain.

How to measure the goodness of representations.

One may view a given dataset as samples of a random vector $\bm{x}$ with a certain distribution in a high-dimensional space, say $\mathbb{R}^{D}$ . Typically, the distribution of $\bm{x}$ has a much lower intrinsic dimension than the ambient space. Generally speaking, learning a representation refers to learning a continuous mapping, say $f(\cdot)$ , that transforms $\bm{x}$ to a so-called feature vector $\bm{z}$ in another (typically lower-dimensional) space, say $\mathbb{R}^{d}$ , where $d<D$ . It is hopeful that through such a mapping

\bm{x}\in\mathbb{R}^{D}\xrightarrow{\hskip 5.69054ptf(\bm{x})\hskip 5.69054pt}\bm{z}\in\mathbb{R}^{d},

(3.4.1)

the low-dimensional intrinsic structures of $\bm{x}$ are identified and represented by $\bm{z}$ in a more compact and structured way so as to facilitate subsequent tasks such as classification or generation. The feature $\bm{z}$ can be viewed as a (learned) compact code for the original data $\bm{x}$ , so the mapping $f$ is also called an encoder. The fundamental question of representation learning is

What is a principled and effective measure for the goodness of representations?

Conceptually, the quality of a representation $\bm{z}$ depends on how well it identifies the most relevant and sufficient information of $\bm{x}$ for subsequent tasks and how efficiently it represents this information. For a long time, it was believed and argued that the “sufficiency” or “goodness” of a learned feature representation should be defined in terms of a specific task. For example, $\bm{z}$ just needs to be sufficient for predicting the class label $\bm{y}$ in a classification problem. Below, let us start with the classic problem of image classification and argue why such a notion of a task-specific “representation” is limited and needs to be generalized.

3.4.1 Linear Discriminative Representations

Suppose that $\bm{x}\in\mathbb{R}^{D}$ is a random vector drawn from a mixture of $K$ (component) distributions $\mathcal{D}=\{\mathcal{D}_{k}\}_{k=1}^{K}$ . Give a finite set of i.i.d. samples $\bm{X}=[\bm{x}_{1},\bm{x}_{2},\ldots,\bm{x}_{N}]\in\mathbb{R}^{D\times N}$ of the random vector $\bm{x}$ , we seek a good representation through a continuous mapping $f(\bm{x}):\mathbb{R}^{D}\rightarrow\mathbb{R}^{d}$ that captures intrinsic structures of $\bm{x}$ and best facilitates the subsequent classification task.²⁵²⁵25Classification is the domain where deep learning demonstrated the initial success, sparking the explosive interest in deep networks. Although our study focuses on classification, we believe the ideas and principles can be naturally generalized to other settings, such as regression. To ease the task of learning distribution $\mathcal{D}$ , in the popular supervised classification setting, a true class label (or a code word for each class), usually represented by a one-hot vector $\bm{y}_{i}\in\mathbb{R}^{K}$ , is given for each sample $\bm{x}_{i}$ .

Encoding class information via cross entropy.

Extensive studies have shown that for many practical datasets (e.g., images, audio, and natural languages), the (encoding) mapping from the data $\bm{x}$ to its class label $\bm{y}$ can be effectively modeled by training a deep network,²⁶²⁶26Here let us not worry about yet which network we should use here and why. The purpose here is to consider any empirically tested deep network. We will leave the justification of the network architectures to the next chapter. here denoted as

f(\bm{x},\theta):\bm{x}\mapsto\bm{y}

with network parameters $\theta\in\Theta$ , where $\Theta$ denotes the parameter space. For the output $f(\bm{x},\theta)$ to match well with the label $\bm{y}$ , we like to minimize the cross-entropy loss over a training set $\{(\bm{x}_{i},\bm{y}_{i})\}_{i=1}^{N}$ :

\min_{\theta\in\Theta}\;-\mathbb{E}[\langle\bm{y},\log(f(\bm{x},\theta))\rangle]\,\approx-\frac{1}{N}\sum_{i=1}^{N}\langle\bm{y}_{i},\log\left(f(\bm{x}_{i},\theta)\right)\rangle.

(3.4.2)

The optimal network parameters $\theta$ are typically found by optimizing the above objective through an efficient gradient descent scheme, with gradients computed via back propagation (BP), as described in Section A.2.3 of Appendix A.

Despite its effectiveness and enormous popularity, there are two serious limitations with this approach: 1) It aims only to predict the labels $\bm{y}$ even if they might be mislabeled. Empirical studies show that deep networks, used as a “black box,” can even fit random labels [ZBH+17]. 2) With such an end-to-end data fitting, despite plenty of empirical efforts in trying to interpret the so-learned features, it is not clear to what extent the intermediate features learned by the network capture the intrinsic structures of the data that make meaningful classification possible in the first place. The precise geometric and statistical properties of the learned features are also often obscured, which leads to the lack of interpretability and subsequent performance guarantees (e.g., generalizability, transferability, and robustness, etc.) in deep learning. Therefore, one of the goals of this section is to address such limitations by reformulating the objective towards learning explicitly meaningful and useful representations for the data $\bm{x}$ , not limited to classification.

Figure 3.18 : Evolution of penultimate layer outputs of a VGG13 neural network when trained on the CIFAR10 dataset with 3 randomly selected classes. Figure from [ PHD20 ] . — Figure 3.18: Evolution of penultimate layer outputs of a VGG13 neural network when trained on the CIFAR10 dataset with 3 randomly selected classes. Figure from [PHD20].

Minimal discriminative features via information bottleneck.

One popular approach to interpret the role of deep networks is to view outputs of intermediate layers of the network as selecting certain latent features $\bm{z}=f(\bm{x},\theta)\in\mathbb{R}^{d}$ of the data that are discriminative among multiple classes. Learned representations $\bm{z}$ then facilitate the subsequent classification task for predicting the class label $\bm{y}$ by optimizing a classifier $g(\bm{z})$ :

\bm{x}\xrightarrow{\hskip 5.69054ptf(\bm{x},\theta)\hskip 5.69054pt}\bm{z}\xrightarrow{\hskip 5.69054ptg(\bm{z})\hskip 5.69054pt}\bm{y}.

(3.4.3)

We know from information theory [CT91] that the mutual information between two random variables, say $\bm{x},\bm{z}$ , is defined to be

I(\bm{x};\bm{z})=H(\bm{x})-H(\bm{x}\mid\bm{z}),

(3.4.4)

where $H(\bm{x}|\bm{z})$ is the conditional entropy of $\bm{x}$ given $\bm{z}$ . The mutual information is also known as the information gain: It measures how much the entropy of the random variable $\bm{x}$ can be reduced once $\bm{z}$ is given. Or equivalently, it measures how much information $\bm{z}$ contains about $\bm{x}$ . The information bottleneck (IB) formulation [TZ15] further hypothesizes that the role of the network is to learn $\bm{z}$ as the minimal sufficient statistics for predicting $\bm{y}$ . Formally, it seeks to maximize the mutual information $I(\bm{z},\bm{y})$ between $\bm{z}$ and $\bm{y}$ while minimizing the mutual information $I(\bm{x},\bm{z})$ between $\bm{x}$ and $\bm{z}$ :

\max_{\theta\in\Theta}\;\mbox{IB}(\bm{x},\bm{y},\bm{z})\doteq I(\bm{z};\bm{y})-\beta I(\bm{x};\bm{z})\quad\ \mathrm{s.t.}\ \bm{z}=f(\bm{x},\theta),

(3.4.5)

where $\beta>0$ .

Given one can overcome some caveats associated with this framework [KTV18], such as how to accurately evaluate mutual information with finite samples of degenerate distributions, this framework can be helpful in explaining certain behaviors of deep networks. For example, recent work [PHD20] indeed shows that the representations learned via the cross-entropy loss (3.4.2) exhibit a neural collapse phenomenon. That is, features of each class are mapped to a one-dimensional vector whereas all other information of the class is suppressed, as illustrated in Figure 3.18.

Remark 3.8.

Neural collapse refers to a phenomenon observed in deep neural networks trained for classification, where the learned feature representations and classifier weights exhibit highly symmetric and structured behavior during the terminal phase of training [PHD20, ZDZ+21]. Specifically, within each class, features collapse to their class mean, and across classes, these means become maximally separated, forming a simplex equiangular configuration. The linear classifier aligns with the class mean up to rescaling. Additionally, the last-layer classifier converges to choosing whichever class has the nearest train class mean. Neural collapse reveals deep connections between optimization dynamics, generalization, and geometric structures arising in supervised learning.

From the above example of classification, we see that the so-learned representation gives a very simple encoder that essentially maps each class of data to only one code word: the one-hot vector representing each class. From the lossy compression perspective, such an encoder is too lossy to preserve information in the data distribution. Other information, such as that useful for tasks such as image generation, is severely lost in such a supervised learning process. To remedy this situation, we want to learn a different encoding scheme such that the resulting feature representation can capture much richer information about the data distribution, not limited to that useful for classification alone.

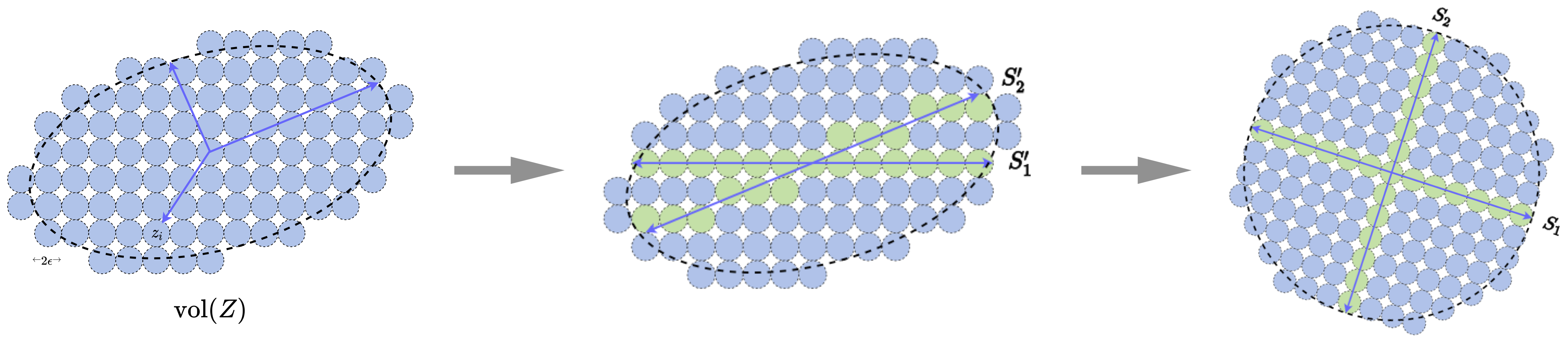
Figure 3.19 : After identifying the low-dimensional data distribution, we would like to further transform the data distribution to a more informative structure representation: R R italic_R is the number of ϵ \epsilon italic_ϵ -balls covering the whole space and R c R^{c} italic_R start_POSTSUPERSCRIPT italic_c end_POSTSUPERSCRIPT is the sum of the numbers for all the subspaces (the green balls). Δ R \Delta R roman_Δ italic_R is their difference (the number of blue balls). — Figure 3.19: After identifying the low-dimensional data distribution, we would like to further transform the data distribution to a more informative structure representation: $R$ is the number of $\epsilon$ -balls covering the whole space and $R^{c}$ is the sum of the numbers for all the subspaces (the green balls). $\Delta R$ is their difference (the number of blue balls).

Linear discriminative representations.

Whether the given data $\bm{X}$ of a mixed distribution $\mathcal{D}$ can be effectively classified or clustered depends on how separable (or discriminative) the component distributions $\mathcal{D}_{k}$ are (or can be made). One popular working assumption is that the distribution of each class has relatively low-dimensional intrinsic structures. Hence we may assume that the distribution $\mathcal{D}_{k}$ of each class has a support on a low-dimensional submanifold, say $\mathcal{M}_{k}$ with dimension $d_{k}\ll D$ , and the distribution $\mathcal{D}$ of $\bm{x}$ is supported on the mixture of those submanifolds, $\mathcal{M}=\cup_{k=1}^{K}\mathcal{M}_{k}$ , in the high-dimensional ambient space $\mathbb{R}^{D}$ .

Not only do we need to identify the low-dimensional distribution, but we also want to represent the distribution in a form that best facilitates subsequent tasks such as classification, clustering, and conditioned generation (as we will see in the future). To do so, we require our learned feature representations to have the following properties:

1.

Within-Class Compressible: Features of samples from the same class should be strongly correlated in the sense that they belong to a low-dimensional linear subspace.
2.

Between-Class Discriminative: Features of samples from different classes should be highly uncorrelated and belong to different low-dimensional linear subspaces.
3.

Maximally Diverse Representation: Dimension (or variance) of the features of each class should be as large as possible as long as they are incoherent to the other classes.

We refer to such a representation the linear discriminative representation (LDR). Notice that the first property aligns well with the objective of the classic principal component analysis (PCA) that we have discussed in Section 2.1.1. The second property resembles that of the classic linear discriminant analysis (LDA) [HTF09]. Figure 3.19 illustrates these properties with a simple example when the data distribution is actually a mixture of two subspaces. Through compression (denoising or clustering), we first identify that the true data distribution is a mixture of two low-dimensional subspaces (middle) instead of a generic Gaussian distribution (left). We then would like to transform the distribution so that the two subspaces eventually become mutually incoherent/independent (right).

Remark 3.9.

Linear discriminant analysis (LDA) [HTF09] is a supervised dimensionality reduction technique that aims to find a linear projection of data that maximizes class separability. Specifically, given labeled data, LDA seeks a linear transformation that projects high-dimensional inputs onto a lower-dimensional space where the classes are maximally separated. Note that PCA is an unsupervised method that projects data onto directions of maximum variance without considering class labels. While PCA focuses purely on preserving global variance structure, LDA explicitly exploits label information to enhance discriminative power; see the comparison in Figure 3.20.

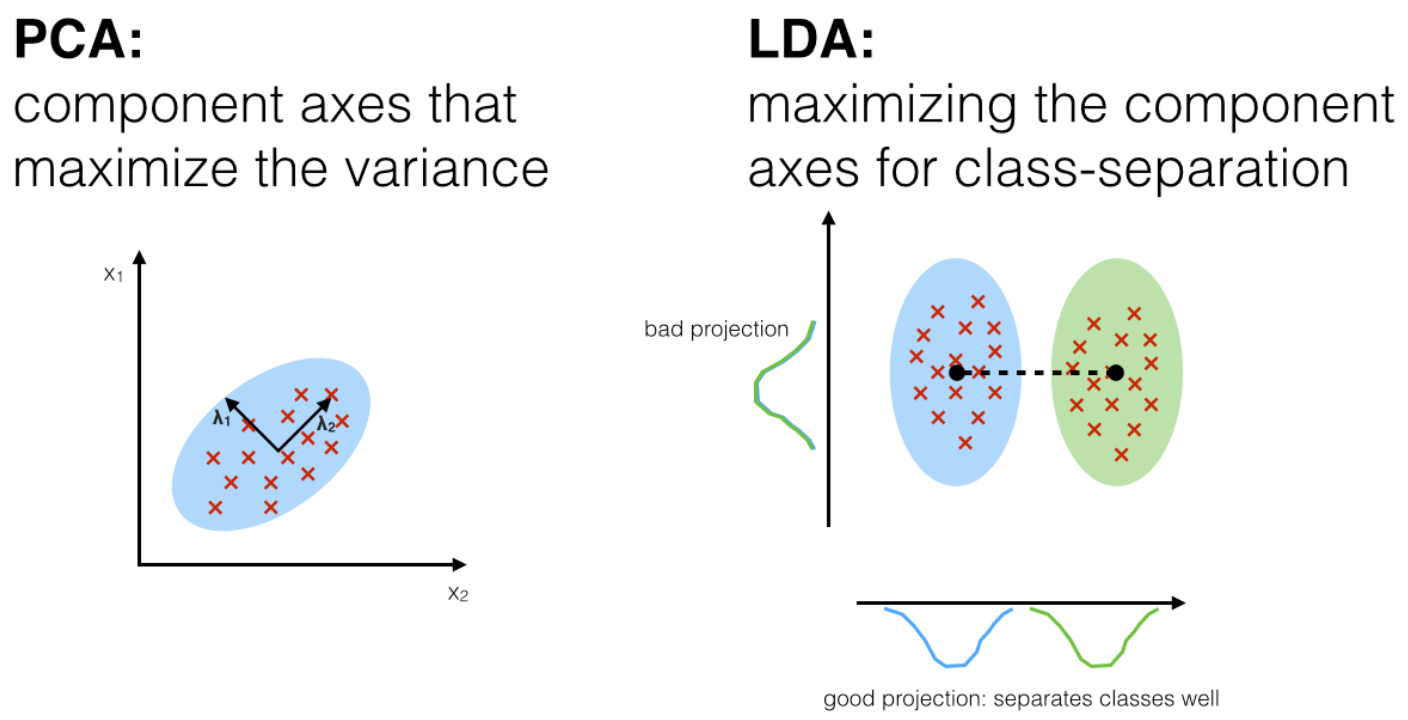
Figure 3.20 : Comparison between PCA and LDA. Figures adpoted from https://sebastianraschka.com/Articles/2014_python_lda.html . — Figure 3.20: Comparison between PCA and LDA. Figures adpoted from https://sebastianraschka.com/Articles/2014_python_lda.html.

The third property is also important because we want the learned features to reveal all possible causes of why one class is different from all other classes. For example, to tell “apple” from “orange”, we care not only about color but also shape and the leaves. Ideally, the dimension of each subspace $\{\mathcal{S}_{k}\}$ should be equal to that of the corresponding submanifold $\mathcal{M}_{k}$ . This property will be important if we would like the map $f(\bm{x},\theta)$ to be invertible for tasks such as image generation. For example, if we draw different sample points from the feature subspace for “apple”, we should be able to decode them to generate diverse images of apples. The feature learned from minimizing the cross entropy (3.4.2) clearly does not have this property.

In general, although the intrinsic structures of each class/cluster may be low-dimensional, they are by no means simply linear (or Gaussian) in their original representation $\bm{x}$ and they need to be made linear first, through some nonlinear transformation.²⁷²⁷27We will discuss how this can be done explicitly in Chapter 5. Therefore, overall, we use the nonlinear transformation $f(\bm{x},\theta)$ to seek a representation of the data such that the subspaces that represent all the classes are maximally incoherent linear subspaces. To be more precise, we want to learn a mapping $\bm{z}=f(\bm{x},\theta)$ that maps each of the submanifolds $\mathcal{M}_{k}\subset\mathbb{R}^{D}$ (Figure 3.21 left) to a linear subspace $\mathcal{S}_{k}\subset\mathbb{R}^{d}$ (Figure 3.21 right). To some extent, the resulting multiple subspaces $\{\mathcal{S}_{k}\}$ can be viewed as discriminative generalized principal components [VMS16] or, if orthogonal, independent components [HO00] of the resulting features $\bm{z}$ for the original data $\bm{x}$ . As we will see in the next Chapter 4, deep networks precisely play the role of modeling and realizing this nonlinear transformation from the data distribution to linear discriminative representations.

3.4.2 The Principle of Maximal Coding Rate Reduction

Although the three properties—between-class discriminative, within-class compressible, and maximally diverse representation—for linear discriminative representations (LDRs) are all highly desired properties of the learned representation $\bm{z}$ , they are by no means easy to obtain: Are these properties compatible so that we can expect to achieve them all at once? If so, is there a simple but principled objective that can measure the goodness of the resulting representations in terms of all these properties? The key to these questions is to find a principled “measure of compactness” or “information gain” for the distribution of a random variable $\bm{z}$ or from its finite samples $\{\bm{z}_{i}\}_{i=1}^{N}$ . Such a measure should directly and accurately characterize intrinsic geometric or statistical properties of the distribution, in terms of its intrinsic dimension or volume. Unlike the cross entropy (3.4.2) or information bottleneck (3.4.5), such a measure should not depend exclusively on class labels so that it can work in more general settings such as supervised, self-supervised, semi-supervised, and unsupervised settings.

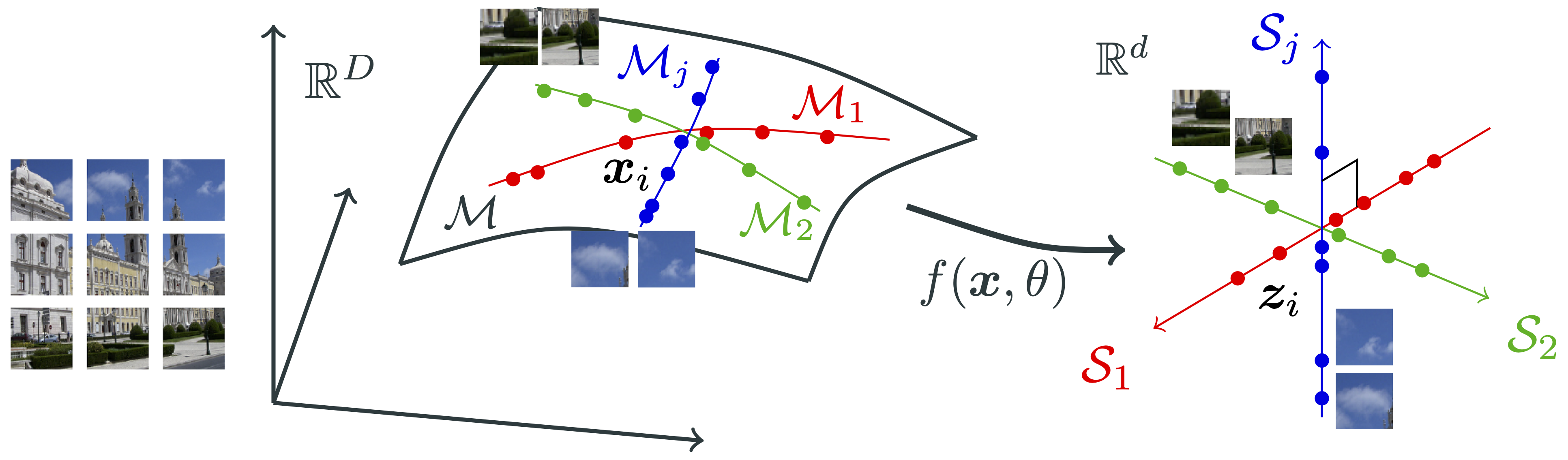
Figure 3.21 : The distribution 𝒟 \mathcal{D} caligraphic_D of high-dimensional data 𝒙 ∈ ℝ D \bm{x}\in\mathbb{R}^{D} bold_italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT is supported on a manifold ℳ \mathcal{M} caligraphic_M and its classes on low-dimensional submanifolds ℳ k \mathcal{M}_{k} caligraphic_M start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT . We aim to learn a mapping f ( 𝒙 , θ ) f(\bm{x},\theta) italic_f ( bold_italic_x , italic_θ ) parameterized by θ \theta italic_θ such that 𝒛 i = f ( 𝒙 i , θ ) \bm{z}_{i}=f(\bm{x}_{i},\theta) bold_italic_z start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT = italic_f ( bold_italic_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT , italic_θ ) lie on a union of maximally uncorrelated subspaces { 𝒮 k } \{\mathcal{S}_{k}\} { caligraphic_S start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT } . — Figure 3.21: The distribution $\mathcal{D}$ of high-dimensional data $\bm{x}\in\mathbb{R}^{D}$ is supported on a manifold $\mathcal{M}$ and its classes on low-dimensional submanifolds $\mathcal{M}_{k}$ . We aim to learn a mapping $f(\bm{x},\theta)$ parameterized by $\theta$ such that $\bm{z}_{i}=f(\bm{x}_{i},\theta)$ lie on a union of maximally uncorrelated subspaces $\{\mathcal{S}_{k}\}$ .

Without loss of generality, assume that the distribution $\mathcal{D}$ of the random vector $\bm{x}$ is supported on a mixture of distributions, i.e., $\mathcal{D}=\cup_{k=1}^{K}\mathcal{D}_{k}$ , where each $\mathcal{D}_{k}\subset\mathbb{R}^{D}$ has a low intrinsic dimension in the high-dimensional ambient space $\mathbb{R}^{D}$ . Let $\bm{X}_{k}\in\mathbb{R}^{D\times N_{k}}$ denote the data matrix whose columns are samples drawn from the distribution $\mathcal{D}_{k}$ , where $N_{k}$ denotes the number of samples for each $k=1,\dots,K$ . Then, we use $\bm{X}=[\bm{X}_{1},\dots,\bm{X}_{K}]\in\mathbb{R}^{D\times N}$ to denote all the samples, where $N=\sum_{k=1}^{K}N_{k}$ . Recall that we also use $\bm{x}_{i}$ to denote the $i$ -th sample of $\bm{X}$ , i.e., $\bm{X}=[\bm{x}_{1},\dots,\bm{x}_{N}]$ . Under an encoding mapping:

\bm{x}\xrightarrow{\hskip 5.69054ptf(\bm{x})\hskip 5.69054pt}\bm{z},

(3.4.6)

the input samples are mapped to $\bm{z}_{i}=f(\bm{x}_{i})$ for each $i=1,\dots,N$ . With an abuse of notation, we also write $\bm{Z}_{k}=f(\bm{X}_{k})$ and $\bm{Z}=f(\bm{X})$ . Therefore, we have $\bm{Z}=[\bm{Z}_{1},\dots,\bm{Z}_{K}]$ and $\bm{Z}=[\bm{z}_{1},\dots\bm{z}_{N}]$ .

On one hand, for learned features to be discriminative, features of different classes/clusters are preferred to be maximally incoherent to each other. Hence, they together should span a space of the largest possible volume (or dimension) and the coding rate of the whole set $\bm{Z}$ should be as large as possible. On the other hand, learned features of the same class/cluster should be highly correlated and coherent. Hence, each class/cluster should only span a space (or subspace) of a very small volume and the coding rate should be as small as possible. Now, we will introduce how to measure the coding rate of the learned features.

Coding rate of features.

Notably, a practical challenge in evaluating the coding rate is that the underlying distribution of the feature representations $\bm{Z}$ is typically unknown. To address this, we may approximate the features $\bm{Z}=[\bm{z}_{1},\ldots,\bm{z}_{N}]$ as samples drawn from a multivariate Gaussian distribution. Under this assumption, as discussed in Section 3.3.3, the compactness of the features $\bm{Z}$ as a whole can be measured in terms of the average coding length per sample, referred to as the coding rate, subject to a precision level $\epsilon>0$ (see (3.3.23)) defined as follows:

R_{\epsilon}(\bm{Z})=\frac{1}{2}\log\det\left(\bm{I}+\frac{d}{N\epsilon^{2}}\bm{Z}\bm{Z}^{\top}\right).

(3.4.7)

On the other hand, we hope that a nonlinear transformation $f(\bm{x})$ maps each class-specific submanifold $\mathcal{M}_{k}\subset\mathbb{R}^{D}$ to a maximally incoherent linear subspace $\mathcal{S}_{k}\subset\mathbb{R}^{d}$ such that the learned features $\bm{Z}$ lie in a union of low-dimensional subspaces. This structure allows for a more accurate evaluation of the coding rate by analyzing each subspace separately. Recall that the columns of $\bm{Z}_{k}$ denotes the features of the samples in $\bm{X}_{k}$ for each $k=1,\dots,K$ . The coding rate for the features in $\bm{Z}_{k}$ can be computed as follows:

\displaystyle R_{\epsilon}(\bm{Z}_{k})=\frac{N_{k}}{2N}\log\det\left(\bm{I}+\frac{d}{N_{k}\epsilon^{2}}\bm{Z}_{k}\bm{Z}_{k}^{\top}\right)

(3.4.8)

Then, the sum of the average coding rates of features in each class is

R_{\epsilon}^{c}(\bm{Z})\doteq\sum_{k=1}^{K}R_{\epsilon}(\bm{Z}_{k}),

(3.4.9)

Therefore, a good representation $\bm{Z}$ of $\bm{X}$ is the one that achieves a large difference between the coding rate for the whole and that for all the classes:

\Delta R_{\epsilon}(\bm{Z})\doteq R_{\epsilon}(\bm{Z})-R_{\epsilon}^{c}(\bm{Z}).

(3.4.10)

Notice that, as per our discussions earlier in this chapter, this difference can be interpreted as the amount of “information gained” by identifying the correct low-dimensional clusters $\bm{Z}_{k}$ within the overall set $\bm{Z}$ .

If we choose our feature mapping $f(\cdot)$ to be a deep neural network $f(\cdot,\theta)$ with network parameters $\theta$ , the overall process of the feature representation and the resulting rate reduction can be illustrated by the following diagram:

\bm{X}\xrightarrow{\hskip 5.69054ptf(\bm{x},\theta)\hskip 5.69054pt}\bm{Z}\xrightarrow{\hskip 5.69054pt\epsilon\hskip 5.69054pt}\Delta R_{\epsilon}(\bm{Z}).

(3.4.11)

Note that $\Delta R_{\epsilon}$ is monotonic in the scale of the features $\bm{Z}$ . To ensure fair comparison across different representations, it is essential to normalize the scale of the learned features. This can be achieved by either imposing the Frobenius norm of each class $\bm{Z}_{k}$ to scale with the number of features in $\bm{Z}_{k}\in\mathbb{R}^{d\times N_{k}}$ , i.e., $\|\bm{Z}_{k}\|_{F}^{2}=N_{k}$ , or by normalizing each feature to be on the unit sphere, i.e., $\bm{z}_{i}\in\mathbb{S}^{d-1}$ , where $N_{k}=\mathrm{tr}(\bm{\Pi}_{k})$ denotes the number of samples in the $k$ -th class. This formulation offers a natural justification for the need for “batch normalization” in the practice of training deep neural networks [IS15].

Once the representations are comparable, the goal becomes to learn a set of features $\bm{Z}=f(\bm{X},\theta)$ such that they maximize the reduction between the coding rate of all features and that of the sum of features w.r.t. their classes:

	$\displaystyle\max_{\theta}$	$\displaystyle\;\Delta R_{\epsilon}\big{(}\bm{Z}\big{)}\doteq R_{\epsilon}(\bm{Z})-R_{\epsilon}^{c}(\bm{Z}),$		(3.4.12)
	s.t.	$\displaystyle\ \ \,\bm{Z}=f(\bm{X},\theta),\ \\|\bm{Z}_{k}\\|_{F}^{2}=N_{k},\ k=1,\dots,K.$		(3.4.12)

We refer to this as the principle of maximal coding rate reduction (MCR²), a true embodiment of Aristotle’s famous quote:

“The whole is greater than the sum of its parts.”

To learn the best representation, we require that the whole is maximally greater than the sum of its parts. Let us examine the example shown in Figure 3.19 again. From a compression perspective, the representation on the right is the most compact one in the sense that the difference between the coding rate when all features are encoded as a single Gaussian (blue) and that when the features are properly clustered and encoded as two separate subspaces (green) is maximal.²⁸²⁸28Intuitively, the ratio between the “volume” of the whole space spanned by all features and that actually occupied by the features is maximal.

Note that the above MCR² principle is designed for supervised learning problems, where the group memberships (or class labels) are known. However, this principle can be naturally extended to unsupervised learning problems by introducing a membership matrix, which encodes the (potentially soft) assignment of each data point to latent groups or clusters. Specifically, let $\bm{\Pi}=\{\bm{\Pi}_{k}\}_{k=1}^{K}\subset\mathbb{R}^{N\times N}$ be a set of diagonal matrices whose diagonal entries encode the membership of the $N$ samples into $K$ classes. That is, $\bm{\Pi}$ lies in a simplex $\Omega\doteq\{\bm{\Pi}:\bm{\Pi}_{k}\geq\bm{0}:\sum_{k=1}^{K}\bm{\Pi}_{k}=\bm{I}_{N}\}$ . Then, we can define the average coding rate with respect to the partition $\bm{\Pi}$ as

\displaystyle R_{\epsilon}^{c}(\bm{Z}\mid\bm{\Pi})\doteq\sum_{k=1}^{K}\frac{\mathrm{tr}(\bm{\Pi}_{k})}{2N}\log\det\left(\bm{I}+\frac{d}{\mathrm{tr}(\bm{\Pi}_{k})\epsilon^{2}}\bm{Z}\bm{\Pi}_{k}\bm{Z}^{\top}\right).

(3.4.13)

When $\bm{Z}$ is given, $R_{\epsilon}^{c}(\bm{Z}|\bm{\Pi})$ is a concave function of $\bm{\Pi}$ . Then the MCR² principle for unsupervised learning problems becomes as follows:

	$\displaystyle\max_{\bm{\Pi},\theta}$	$\displaystyle\ \Delta R_{\epsilon}\big{(}\bm{Z}\mid\bm{\Pi})\doteq R_{\epsilon}(\bm{Z})-R_{\epsilon}^{c}(\bm{Z}\mid\bm{\Pi})$
	$\displaystyle\mathrm{s.t.}$	$\displaystyle\ \ \ \bm{Z}=f(\bm{X},\theta),\ \\|\bm{Z}\bm{\Pi}_{k}\\|_{F}^{2}=N_{k},\ k=1,\dots,K,\ \bm{\Pi}\in\Omega.$		(3.4.14)

Compared to (3.4.12), the formulation here allows for the joint optimization of both the group memberships and the network parameters. In particular, when $\bm{\Pi}$ is fixed to a group membership matrix that assigns $N$ data points into $K$ groups, Problem (3.4.2) can recover Problem (3.4.12).

Figure 3.22 : Local optimization landscape: According to Theorem • ‣ 3.7 , the global maximum of the rate reduction objective corresponds to a solution with mutually incoherent subspaces. — Figure 3.22: Local optimization landscape: According to Theorem • ‣ 3.7, the global maximum of the rate reduction objective corresponds to a solution with mutually incoherent subspaces.

3.4.3 Optimization Properties of Coding Rate Reduction

In this subsection, we study the optimization properties of the MCR² function by analyzing its optimal solutions and the structure of its optimization landscape. To get around the technical difficulty introduced by the neural networks, we consider a simplified version of Problem (3.4.12) as follows:

\displaystyle\max_{\bm{Z}}\ R_{\epsilon}(\bm{Z})-R_{\epsilon}^{c}(\bm{Z})\qquad\mathrm{s.t.}\quad\|\bm{Z}_{k}\|_{F}^{2}=N_{k},\ k=1,\dots,K.

(3.4.15)

In theory, the MCR² principle (3.4.15) benefits from great generalizability and can be applied to representations $\bm{Z}$ of any distributions as long as the rates $R_{\epsilon}$ and $R^{c}_{\epsilon}$ for the distributions can be accurately and efficiently evaluated. The optimal representation $\bm{Z}^{\ast}$ should have some interesting geometric and statistical properties. We here reveal nice properties of the optimal representation with the special case of subspaces, which have many important use cases in machine learning. When the desired representation for $\bm{Z}$ is multiple subspaces, the rates $R_{\epsilon}$ and $R^{c}_{\epsilon}$ in (3.4.15) are given by (3.4.7) and (3.4.9), respectively. At the maximal rate reduction, MCR² achieves its optimal representations, denoted as $\bm{Z}^{\ast}=[\bm{Z}_{1}^{*},\dots,\bm{Z}_{K}^{*}]$ with $\operatorname{rank}{(\bm{Z}_{k}^{*})}\leq d_{k}$ . One can show that $\bm{Z}^{\ast}$ has the following desired properties (see [YCY+20] for a formal statement and detailed proofs).

Theorem 3.7 (Characterization of Global Optimal Solutions).

Suppose $\bm{Z}^{\ast}=[\bm{Z}_{1}^{*},\dots,\bm{Z}_{K}^{*}]$ is a global optimal solution of Problem (3.4.15). The following statements hold:

•

Between-Class Discriminative: As long as the ambient space is adequately large ( $d\geq\sum_{k=1}^{K}d_{k}$ ), the subspaces are all orthogonal to each other, i.e., $(\bm{Z}_{k}^{*})^{\top}\bm{Z}_{l}^{*}=\bm{0}$ for $k\not=l$ .
•

Maximally Diverse Representation: As long as the coding precision is adequately high, i.e., $\epsilon^{4}<c\cdot\min_{k}\left\{\frac{N_{k}}{N}\frac{d^{2}}{d_{k}^{2}}\right\}$ , where $c>0$ is a constant. Each subspace achieves its maximal dimension, i.e. $\mathrm{rank}{(\bm{Z}_{k}^{*})}=d_{k}$ . In addition, the largest $d_{k}-1$ singular values of $\bm{Z}_{k}^{*}$ are equal.

This theorem indicates that the MCR² principle promotes embedding of data into multiple independent subspaces (as illustrated in Figure 3.22), with features distributed isotropically in each subspace (except for possibly one dimension). Notably, this theorem also confirms that the features learned by the MCR² principle exhibit the desired low-dimensional discriminative properties discussed in Section 3.4.1. In addition, among all such discriminative representations, it prefers the one with the highest dimensions in the ambient space. This is substantially different from the objective of information bottleneck (3.4.5).

Example 3.13 (Classification of Images on CIFAR-10).

We here present how the MCR² objective helps learn better representations than the cross entropy (3.4.2) for image classification. Here we adopt the popular neural network architecture, the ResNet-18 [HZR+16a], to model the feature mapping $\bm{z}=f(\bm{x},\theta)$ . We optimize the neural network parameters $\theta$ to maximize the coding rate reduction. We evaluate the performance with the CIFAR10 image classification dataset [KH+09].

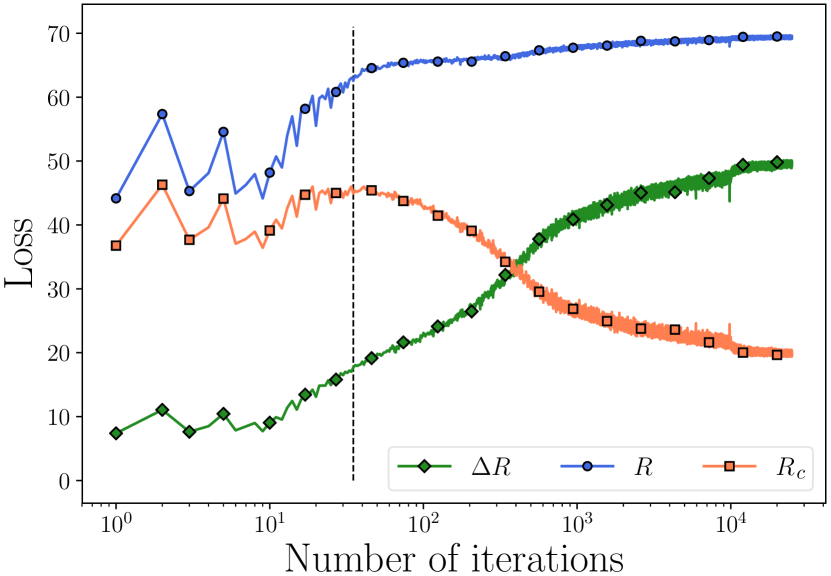
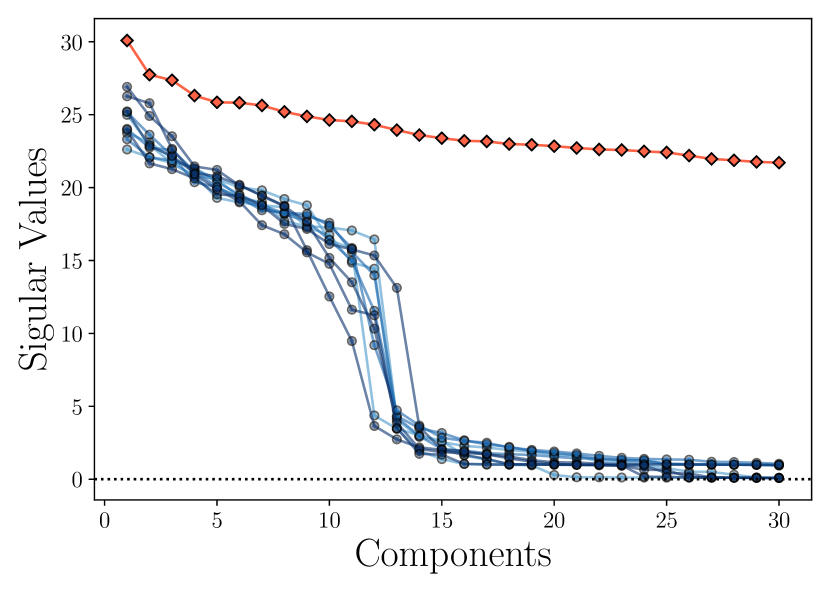
(a) Evolution of R ϵ R_{\epsilon} italic_R start_POSTSUBSCRIPT italic_ϵ end_POSTSUBSCRIPT , R ϵ c R^{c}_{\epsilon} italic_R start_POSTSUPERSCRIPT italic_c end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_ϵ end_POSTSUBSCRIPT , Δ R ϵ \Delta R_{\epsilon} roman_Δ italic_R start_POSTSUBSCRIPT italic_ϵ end_POSTSUBSCRIPT during the training process. — (a) Evolution of $R_{\epsilon}$ , $R^{c}_{\epsilon}$ , $\Delta R_{\epsilon}$ during the training process.

Figure 3.24 : Cosine similarity between learned features by using the MCR 2 objective ( left ) and CE loss ( right ). — Figure 3.24: Cosine similarity between learned features by using the MCR² objective (left) and CE loss (right).

Figure 3.23(a) illustrates how the two rates and their difference (for both training and test data) evolve over epochs of training: After an initial phase, $R_{\epsilon}$ gradually increases while $R^{c}_{\epsilon}$ decreases, indicating that features $\bm{Z}$ are expanding as a whole while each class $\bm{Z}_{k}$ is being compressed. Figure 3.23(b) shows the distribution of singular values per $\bm{Z}_{k}$ . Figure 3.24 shows the cosine similarities between the learned features sorted by class. We compare the similarities of the learned features by using the cross-entropy (3.4.2) and the MCR² objective (3.4.12). From the plots, one can clearly see that the representations learned by using MCR² loss are much more diverse than the ones learned by using cross-entropy loss. More details of this experiment can be found in [CYY+22]. $\blacksquare$

However, there has been an apparent lack of justification of the network architectures used in the above experiments. It is yet unclear why the network adopted here (the ResNet-18) is suitable for representing the map $f(\bm{x},\theta)$ , let alone for interpreting the layer operators and parameters $\theta$ learned inside. In the next chapter, we will show how to derive network architectures and components entirely as a “white box” from the desired objective (say the rate reduction).

Regularized MCR².

The above theorem characterizes properties of the global optima of the rate reduction objectives. What about other optima, such as local ones? Due to the constraints of the Frobenius norm, it is a difficult task to analyze Problem (3.4.15) from an optimization-theoretic perspective. Therefore, we consider the Lagrangian formulation of (3.4.15). This can be viewed as a tight relaxation or even an equivalent problem of (3.4.15) whose optimal solutions agree under specific settings of the regularization parameter; see [WLP+24, Proposition 1]. Specifically, the formulation we study, referred to henceforth as the regularized MCR² problem, is as follows:

\displaystyle\max_{\bm{Z}}\ R_{\epsilon}(\bm{Z})-R_{\epsilon}^{c}(\bm{Z})-\frac{\lambda}{2}\|\bm{Z}\|_{F}^{2},

(3.4.16)

where $\lambda>0$ is the regularization parameter. Although the program (3.4.16) is highly nonconcave and involves matrix inverses in its gradient computation, we can still explicitly characterize its local and global optima as follows.

Theorem 3.8 (Local and Global Optima).

Let $N_{k}$ denote the number of training samples in the $k$ -th class for each $k\in\{1,\dots,K\}$ , $N_{\max}\doteq\max\{N_{1},\dots,N_{K}\}$ , $\alpha=d/(N\epsilon^{2})$ , and $\alpha_{k}=d/(N_{k}\epsilon^{2})$ for each $k\in\{1,\dots,K\}$ . Given a coding precision $\epsilon>0$ , if the regularization parameter satisfies

\displaystyle\lambda\in\left(0,\frac{d(\sqrt{N/N_{\max}}-1)}{N(\sqrt{N/N_{\max}}+1)\epsilon^{2}}\right],

(3.4.17)

then the following statements hold:
(i) (Local maximizers) $\bm{Z}^{*}=\left[\bm{Z}_{1}^{*},\dots,\bm{Z}_{K}^{*}\right]$ is a local maximizer of Problem (3.4.16) if and only if the $k$ -th block admits the following decomposition

\displaystyle\bm{Z}_{k}^{*}=\left(\frac{\eta_{k}+\sqrt{\eta_{k}^{2}-4\lambda^{2}N/N_{k}}}{2\lambda\alpha_{k}}\right)^{1/2}\bm{U}_{k}\bm{V}_{k}^{\top},

(3.4.18)

where (a) $r_{k}=\mathrm{rank}(\bm{Z}_{k}^{*})$ satisfies $r_{k}\in[0,\min\{N_{k},d\})$ and $\sum_{k=1}^{K}r_{k}\leq\min\{N,d\}$ , (b) $\bm{U}_{k}\in\mathcal{O}^{d\times r_{k}}$ satisfies $\bm{U}_{k}^{\top}\bm{U}_{l}=\bm{0}$ for all $k\neq l$ , $\bm{V}_{k}\in\mathcal{O}^{N_{k}\times r_{k}}$ , and (c) $\eta_{k}=(\alpha_{k}-\alpha)-\lambda(N/N_{k}+1)$ for each $k\in\{1,\dots,K\}$ .
(ii) (Global maximizers) $\bm{Z}^{*}=\left[\bm{Z}_{1}^{*},\dots,\bm{Z}_{K}^{*}\right]$ is a global maximizer of Problem (3.4.16) if and only if (a) it satisfies the above all conditions and $\sum_{k=1}^{K}r_{k}=\min\{m,d\}$ , and (b) for all $k\neq l\in[K]$ satisfying $N_{k}<N_{l}$ and $r_{l}>0$ , we have $r_{k}=\min\{N_{k},d\}$ .

Figure 3.25 : Global optimization landscape: According to [ SQW15 , LSJ+16 ] , Theorems 3.8 and 3.9 , both global and local maxima of the (regularized) rate reduction objective correspond to a solution with mutually incoherent subspaces. All other critical points are strict saddle points. — Figure 3.25: Global optimization landscape: According to [SQW15, LSJ+16], Theorems 3.8 and 3.9, both global and local maxima of the (regularized) rate reduction objective correspond to a solution with mutually incoherent subspaces. All other critical points are strict saddle points.

This theorem explicitly characterizes the local and global optima of problem (3.4.16). Intuitively, this shows that the features represented by each local maximizer of Problem (3.4.16) are low-dimensional and discriminative. Although we have characterized the local and global optimal solutions in Theorem 3.8, it remains unknown whether these solutions can be efficiently computed using GD to solve the problem (3.4.16), since GD may get stuck at other critical points such as a saddle point. Fortunately, [SQW15, LSJ+16] showed that if a function is twice continuously differentiable and satisfies the strict saddle property, i.e., each critical point is either a local minimizer or a strict saddle point²⁹²⁹29We say that a critical point is a strict saddle point of Problem (3.4.16) if it has a direction with strictly positive curvature [SQW15]. This includes classical saddle points with strictly positive curvature as well as local minimizers., GD converges to its local minimizer almost surely with random initialization. We investigate the global optimization landscape of the problem (3.4.16) by characterizing all its critical points as follows.

Theorem 3.9 (Benign Global Optimization Landscape).

Given a coding precision $\epsilon>0$ , if the regularization parameter satisfies (3.4.17), it holds that any critical point $\bm{Z}$ of the problem (3.4.16) is either a local maximizer or a strict saddle point.

Together, the above two theorems show that the learned features associated with each local maximizer of the rate reduction objective—not just global maximizers—are structured as incoherent low-dimensional subspaces. Furthermore, the (regularized) rate reduction objective (3.4.12) has a very benign landscape with only local maxima and strict saddles as critical points, as illustrated in Figure 3.25. According to [SQW15, LSJ+16], Theorems 3.8 and 3.9 imply that low-dimensional and discriminative representations (LDRs) can be efficiently found by applying (stochastic) gradient descent to the rate reduction objective (3.4.12) from random initialization. These results also indirectly explain why in Figure 3.24, if the chosen network is expressive enough and trained well, the resulting representation typically gives an incoherent linear representation that likely corresponds to the globally optimal solution. Interested readers are referred to [WLP+24] for proofs.

3.5 Summary and Notes

The use of denoising and diffusion for sampling has a rich history. The first work which is clearly about a diffusion model is probably [SWM+15], but before this there are many works about denoising as a computational and statistical problem. The most relevant of these is probably [Hyv05], which explicitly uses the score function to denoise (as well as perform independent component analysis). The most popular follow-ups are basically co-occurring: [HJA20, SE19]. Since then, thousands of papers have built on diffusion models; we will revisit this topic in Chapter 5.

Many of these works use a different stochastic process than the simple linear combination (3.2.69). In fact, all works listed above emphasize the need to add independent Gaussian noise at the beginning of each step of the forward process. Theoretically-minded work actually uses Brownian motion or stochastic differential equations to formulate the forward process [SSK+21]. However, since linear combinations of Gaussians still result in Gaussians, the marginal distributions of such processes still take the form of (3.2.69). Most of our discussion requires only that the marginal distributions are what they are, and hence our overly simplistic model is actually quite enough for almost everything. In fact, the only time where marginal distributions are not enough is when we derive an expression for $\operatorname{\mathbb{E}}[\bm{x}_{s}\mid\bm{x}_{t}]$ in terms of $\operatorname{\mathbb{E}}[\bm{x}\mid\bm{x}_{t}]$ . Different (noising) processes give different such expressions, which can be used for sampling (and of course there are other ways to derive efficient samplers, such as the ever-popular DDPM sampler). The process in (3.2.69) is a bona fide stochastic process, however, whose “natural” denoising iteration takes the form of the popular DDIM algorithm [SME20]. (Even this equivalence is not trivial; we cite [DGG+25] as a justification.)

On top of the theoretical work [LY24] covered in Section 1.3.1, and the lineage of work that it builds on, which studies the sampling efficiency of diffusion models when the data has low-dimensional structure, there is a large body of work which studies the training efficiency of diffusion models when the data has low-dimensional structure. Specifically, [CHZ+23] and [WZZ+24] characterized the approximation and estimation error of denoisers when the data belongs to a mixture of low-rank Gaussians, showing that the number of training samples required to accurately learn the distribution scales with the intrinsic dimension of the data rather than the ambient distribution. There is considerable methodological work which attempts to utilize the low-dimensional structure of the data in order to do various things with diffusion models. We highlight three here: image editing [CZG+24], watermarking [LZQ24], and unlearning [CZL+25], though as always this is an inexhaustive list.

3.6 Exercises and Extensions

Exercise 3.1.

Please show that (3.2.4) is the optimal solution of Problem (3.2.3).

Exercise 3.2.

Consider random vectors $\bm{x}\in\mathbb{R}^{D}$ and $\bm{y}\in\mathbb{R}^{d}$ , such that the pair $(\bm{x},\bm{y})\in\mathbb{R}^{D+d}$ is jointly Gaussian. This means that

\begin{bmatrix}\bm{x}\\ \bm{y}\end{bmatrix}\sim\mathcal{N}\left(\begin{bmatrix}\bm{\mu}_{\bm{x}}\\ \bm{\mu}_{\bm{y}}\end{bmatrix},\begin{bmatrix}\bm{\Sigma}_{\bm{x}}&\bm{\Sigma}_{\bm{x}\bm{y}}\\ \bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\bm{\Sigma}_{\bm{y}}\end{bmatrix}\right),

where the mean and covariance parameters are given by

\bm{\mu}_{\bm{x}}=\mathbb{E}[\bm{x}],\quad\bm{\mu}_{\bm{y}}=\mathbb{E}[\bm{y}],\quad\begin{bmatrix}\bm{\Sigma}_{\bm{x}}&\bm{\Sigma}_{\bm{x}\bm{y}}\\ \bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\bm{\Sigma}_{\bm{y}}\end{bmatrix}=\mathbb{E}\left[\begin{bmatrix}\bm{x}-\mathbb{E}[\bm{x}]\\ \bm{y}-\mathbb{E}[\bm{y}]\end{bmatrix}\begin{bmatrix}\bm{x}-\mathbb{E}[\bm{x}]\\ \bm{y}-\mathbb{E}[\bm{y}]\end{bmatrix}^{\top}\right]

Assume that $\bm{\Sigma}_{\bm{y}}$ is positive definite (hence invertible); then positive semidefiniteness of the covariance matrix is equivalent to the Schur complement condition $\bm{\Sigma}_{\bm{x}}-\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}\bm{\Sigma}_{\bm{x}\bm{y}}^{\top}\succeq\mathbf{0}$ .

In this exercise, we will prove that the conditional distribution $p_{\bm{x}\mid\bm{y}}$ is Gaussian: namely,

p_{\bm{x}\mid\bm{y}}\sim\mathcal{N}\left(\bm{\mu}_{\bm{x}}+\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}(\bm{y}-\bm{\mu}_{\bm{y}}),\bm{\Sigma}_{\bm{x}}-\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}\bm{\Sigma}_{\bm{x}\bm{y}}^{\top}\right).

(3.6.1)

A direct path to prove this result manipulates the defining ratio of densities $p_{\bm{x},\bm{y}}/p_{\bm{y}}$ . We sketch an algebraically-concise argument of this form below.

Verify the following matrix identity for the covariance:

\begin{bmatrix}\bm{\Sigma}_{\bm{x}}&\bm{\Sigma}_{\bm{x}\bm{y}}\\ \bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\bm{\Sigma}_{\bm{y}}\end{bmatrix}=\begin{bmatrix}\bm{I}_{D}&\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}\\ \mathbf{0}&\bm{I}_{d}\end{bmatrix}\begin{bmatrix}\bm{\Sigma}_{\bm{x}}-\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}\bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\mathbf{0}\\ \mathbf{0}&\bm{\Sigma}_{\bm{y}}\end{bmatrix}\begin{bmatrix}\bm{I}_{D}&\mathbf{0}\\ \bm{\Sigma}_{\bm{y}}^{-1}\bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\bm{I}_{d}\end{bmatrix}.

(3.6.2)

One arrives at this identity by performing two rounds of (block) Gaussian elimination on the covariance matrix.

Based on the previous identity, show that

\begin{bmatrix}\bm{\Sigma}_{\bm{x}}&\bm{\Sigma}_{\bm{x}\bm{y}}\\ \bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\bm{\Sigma}_{\bm{y}}\end{bmatrix}^{-1}=\begin{bmatrix}\bm{I}_{D}&\mathbf{0}\\ -\bm{\Sigma}_{\bm{y}}^{-1}\bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\bm{I}_{d}\end{bmatrix}\begin{bmatrix}\left(\bm{\Sigma}_{\bm{x}}-\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}\bm{\Sigma}_{\bm{x}\bm{y}}^{\top}\right)^{-1}&\mathbf{0}\\ \mathbf{0}&\bm{\Sigma}_{\bm{y}}^{-1}\end{bmatrix}\begin{bmatrix}\bm{I}_{D}&-\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}\\ \mathbf{0}&\bm{I}_{d}\end{bmatrix}

(3.6.3)

whenever the relevant inverses are defined.³⁰³⁰30In cases where the Schur complement term is not invertible, the same result holds with its inverse replaced by the Moore-Penrose pseudoinverse. In particular, the conditional distribution (3.6.1) becomes a degenerate Gaussian distribution. Conclude that

	$\displaystyle\begin{bmatrix}\bm{x}-\bm{\mu}_{\bm{x}}\\ \bm{y}-\bm{\mu}_{\bm{y}}\end{bmatrix}^{\top}\begin{bmatrix}\bm{\Sigma}_{\bm{x}}&\bm{\Sigma}_{\bm{x}\bm{y}}\\ \bm{\Sigma}_{\bm{x}\bm{y}}^{\top}&\bm{\Sigma}_{\bm{y}}\end{bmatrix}^{-1}\begin{bmatrix}\bm{x}-\bm{\mu}_{\bm{x}}\\ \bm{y}-\bm{\mu}_{\bm{y}}\end{bmatrix}$		(3.6.4)
	$\displaystyle\qquad=\begin{bmatrix}\bm{x}-\left(\bm{\mu}_{\bm{x}}+\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}(\bm{y}-\bm{\mu}_{\bm{y}})\right)\\ \bm{y}-\bm{\mu}_{\bm{y}}\end{bmatrix}^{\top}\begin{bmatrix}\left(\bm{\Sigma}_{\bm{x}}-\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}\bm{\Sigma}_{\bm{x}\bm{y}}^{\top}\right)^{-1}&\mathbf{0}\\ \mathbf{0}&\bm{\Sigma}_{\bm{y}}^{-1}\end{bmatrix}\begin{bmatrix}\bm{x}-\left(\bm{\mu}_{\bm{x}}+\bm{\Sigma}_{\bm{x}\bm{y}}\bm{\Sigma}_{\bm{y}}^{-1}(\bm{y}-\bm{\mu}_{\bm{y}})\right)\\ \bm{y}-\bm{\mu}_{\bm{y}}\end{bmatrix}.$		(3.6.5)

(Hint: To economize algebraic manipulations, note that the first and last matrices on the RHS of Equation 3.6.2 are transposes of one another.)

3.

By dividing $p_{\bm{x},\bm{y}}/p_{\bm{y}}$ , prove Equation 3.6.1. (Hint: Using the previous identities, only minimal algebra should be necessary. For the normalizing constant, use Equation 3.6.3 to factor the determinant similarly.)

Exercise 3.3.

Show the Sherman-Morrison-Woodbury identity, i.e., for matrices $\bm{A}$ , $\bm{C}$ , $\bm{U}$ , $\bm{V}$ such that $\bm{A}$ , $\bm{C}$ , and $\bm{A}+\bm{U}\bm{C}\bm{V}$ are invertible,

(\bm{A}+\bm{U}\bm{C}\bm{V})^{-1}=\bm{A}^{-1}-\bm{A}^{-1}\bm{U}(\bm{C}^{-1}+\bm{V}\bm{A}^{-1}\bm{U})^{-1}\bm{V}\bm{A}^{-1}

(3.6.6)

Exercise 3.4.

Rederive the following, assuming $\bm{x}_{t}$ follows the generalized noise model (3.2.69).

•

Tweedie’s formula: (3.2.70).
•

The DDIM iteration: (3.2.71).
•

The Bayes optimal denoiser for a Gaussian mixture model: (3.2.72).

Exercise 3.5.

1.

Implement the formulae derived in Exercise 3.4, building a sampler for Gaussian mixtures.
2.

Reproduce Figure 3.4 and Figure 3.7.

We now introduce a separate process called Flow Matching (FM), as follows:

\alpha_{t}=1-t,\qquad\sigma_{t}=t.

(3.6.7)

Implement this process using the same framework, and test it for sampling in high dimensions. Which process seems to give better or more stable results?

Exercise 3.6.

Please show the following properties of the $\log\det(\cdot)$ function.

1.

Show that

$\displaystyle f(\bm{X})=\log\det\left(\bm{X}\right)$

is a concave function. (Hint: The function $f(\bm{x})$ is convex if and only if the function $f(\bm{x}+t\bm{h})$ for all $\bm{x}$ and $\bm{h}$ .)

Show that:

\displaystyle\log\det(\bm{I}+\bm{X}^{\top}\bm{X})=\log\det(\bm{I}+\bm{X}\bm{X}^{\top})

Let $\bm{A}\in\mathbb{R}^{n\times n}$ be a positive definite matrix. Please show that:

\displaystyle\log\det\left(\bm{A}\right)=\sum_{i=1}^{n}\log(\lambda_{i}),

(3.6.8)

where $\lambda_{1},\lambda_{2},\dots,\lambda_{n}$ are the eigenvalues of $\bm{A}$ .

Chapter 3 Pursuing Low-Dimensionality via Lossy Compression

3.1 Entropy Minimization and Compression

3.1.1 Entropy and Coding Rate

3.1.2 Differential Entropy

Example 3.1 (Entropy of Gaussian Distributions).

3.1.3 Minimizing Coding Rate

Theorem 3.1 (Information Inequality).

Proof.

3.2 Compression via Denoising

3.2.1 Diffusion and Denoising Processes

Theorem 3.2 (Simplified Version of Theorem B.2).

Example 3.2 (Denoising Gaussian Noise from a Mixture of Gaussians).

Theorem 3.3 (Tweedie’s Formula).

Proof.

Example 3.3 (Denoising a Two-Point Mixture).

Theorem 3.4 (Simplified Version of Theorem B.3).

Remark 3.1.

3.2.2 Learning and Sampling a Distribution via Iterative Denoising

Step 1: different discretizations.

Step 2: different noise models.

Step 3: optimizing training pipelines.

(Optional) Step 4: changing the estimation target.

Theorem 3.5 ([LY24] Theorem 1, Simplified).

Remark 3.2.

Remark 3.3.

Remark 3.4.

3.3 Compression via Lossy Coding

3.3.1 Necessity of Lossy Coding

Example 3.4 (Volume, Dimension, and Entropy).

Example 3.5 (Density).

Example 3.6 (Precision).

3.3.2 Rate Distortion and Data Geometry

Remark 3.5.

Remark 3.6.

Example 3.7.

Theorem 3.6.

Proof.

Remark 3.7.

3.3.3 Lossy Coding Rate for a Low-Dimensional Gaussian

Example 3.8.

3.3.4 Clustering a Mixture of Low-Dimensional Gaussians

Example 3.9.

The clustering problem.

Clustering via lossy compression.

Example 3.10.

Example 3.11.

Optimization strategies to cluster.

Example 3.12 (Image Segmentation).

3.4 Maximizing Information Gain

How to measure the goodness of representations.

3.4.1 Linear Discriminative Representations

Encoding class information via cross entropy.

Minimal discriminative features via information bottleneck.

Remark 3.8.

Linear discriminative representations.

Remark 3.9.

3.4.2 The Principle of Maximal Coding Rate Reduction

Coding rate of features.

3.4.3 Optimization Properties of Coding Rate Reduction

Theorem 3.7 (Characterization of Global Optimal Solutions).

Example 3.13 (Classification of Images on CIFAR-10).

Regularized MCR2.

Theorem 3.8 (Local and Global Optima).

Theorem 3.9 (Benign Global Optimization Landscape).

3.5 Summary and Notes

3.6 Exercises and Extensions

Exercise 3.1.

Exercise 3.2.

Exercise 3.3.

Exercise 3.4.

Exercise 3.5.

Exercise 3.6.

Regularized MCR².