Chapter 6 Inference with Low-Dimensional Distributions

In this chapter

Bayesian Inference and Constrained Optimization
Conditional Inference with a Known Data Distribution
Conditional Inference with a Learned Data Representation
Image Completion with Masked Auto-Encoding Conditional Sampling with Measurement Matching Body Pose Generation Conditioned on Head and Hands
Conditional Inference with Paired Data and Measurements
Class Conditioned Image Generation Caption Conditioned Image Generation
Conditional Inference with Measurement Self-Consistency
Linear Measurement Models 3D Visual Model from Calibrated Images
Summary and Notes
Exercises and Extensions

“Mathematics is the art of giving the same name to different things.”

— Henri Poincaré

In the previous chapters of this book, we have studied how to effectively and efficiently learn a representation for a variable $\bm{x}$ in the world with a distribution $p(\bm{x})$ that has a low-dimensional support in a high-dimensional space. So far, we have mainly developed the methodology for learning representation and autoencoding in a general, distribution or task-agnostic fashion. With such a learned representation, one can already use it to perform some generic and basic tasks such as classification (if the encoding is supervised with the class) and generation of random samples that have the same distribution as the given data (say natural images or natural languages).

More generally, however, the universality and scalability of the theoretical and computational framework presented in this book has enabled us to learn the distribution of a variety of important real-world high-dimensional data such as natural languages, human poses, natural images, videos, and even 3D scenes. Once the intrinsically rich and low-dimensional structures of these real data can be learned and represented correctly, they start to enable a broad family of powerful, often seemingly miraculous, tasks. Hence, from here onwards, we will start to show how to connect and tailor the general methods presented in previous chapters to learn useful representations for specific structured data distributions and for many popular tasks in modern practice of machine intelligence.

6.1 Bayesian Inference and Constrained Optimization

Leveraging Low-dimensionality for Stable and Robust Inference.

Generally speaking, a good representation or autoencoding should enable us to utilize the learned low-dimensional distribution of the data $\bm{x}$ and its representation $\bm{z}$ for various subsequent classification, estimation, and generation tasks under different conditions. As we have alluded to earlier in Chapter 1 Section 1.2.2, the importance of the low-dimensionality of the distribution is the key for us to conduct stable and robust inference related to the data $\bm{x}$ , as illustrated by the few simple examples in Figure 1.9, from incomplete, noisy, and even corrupted observations. As it turns out, the very same concept carries over to real-world high-dimensional data whose distributions have a low-dimensional support, such as natural images and languages.

Despite a dazzling variety of applications in the practice of machine learning with data such as languages, images, videos and many other modalities, almost all practical applications can be viewed as a special case of the following inference problem: given an observation $\bm{y}$ that depends on $\bm{x}$ , say

\bm{y}=h(\bm{x})+\bm{w},

(6.1.1)

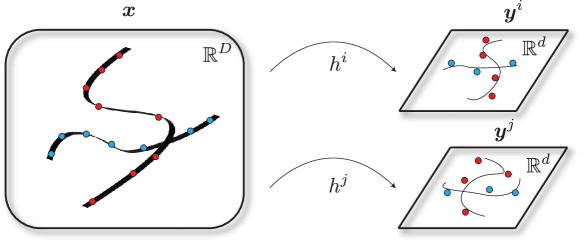
where $h(\cdot)$ represents measurements of a part of $\bm{x}$ or certain observed attributes and $\bm{w}$ represents some measurement noise and even (sparse) corruptions, solve the “inverse problem” of obtaining a most likely estimate $\hat{\bm{x}}(\bm{y})$ of $\bm{x}$ or generating a sample $\hat{\bm{x}}$ that is at least consistent with the observation $\bm{y}\approx h(\hat{\bm{x}})$ . Figure 6.1 illustrates the general relationship between $\bm{x}$ and $\bm{y}$ .

Figure 6.1 : Inference with low-dimensional distributions. This is the generic picture for this chapter: we have a low-dimensional distribution for 𝒙 ∈ ℝ D \bm{x}\in\mathbb{R}^{D} bold_italic_x ∈ blackboard_R start_POSTSUPERSCRIPT italic_D end_POSTSUPERSCRIPT (here depicted as a union of two 2 2 2 -dimensional manifolds in ℝ 3 \mathbb{R}^{3} blackboard_R start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT ) and a measurement model 𝒚 = h ( 𝒙 ) + 𝒘 ∈ ℝ d \bm{y}=h(\bm{x})+\bm{w}\in\mathbb{R}^{d} bold_italic_y = italic_h ( bold_italic_x ) + bold_italic_w ∈ blackboard_R start_POSTSUPERSCRIPT italic_d end_POSTSUPERSCRIPT . We want to infer various things about this model, including the conditional distribution of 𝒙 \bm{x} bold_italic_x given 𝒚 \bm{y} bold_italic_y , or the conditional expectation 𝔼 [ 𝒙 ∣ 𝒚 ] \mathbb{E}[\bm{x}\mid\bm{y}] blackboard_E [ bold_italic_x ∣ bold_italic_y ] , given various information about the model and (potentially finite) samples of either 𝒙 \bm{x} bold_italic_x or 𝒚 \bm{y} bold_italic_y . — Figure 6.1: Inference with low-dimensional distributions. This is the generic picture for this chapter: we have a low-dimensional distribution for $\bm{x}\in\mathbb{R}^{D}$ (here depicted as a union of two $2$ -dimensional manifolds in $\mathbb{R}^{3}$ ) and a measurement model $\bm{y}=h(\bm{x})+\bm{w}\in\mathbb{R}^{d}$ . We want to infer various things about this model, including the conditional distribution of $\bm{x}$ given $\bm{y}$ , or the conditional expectation $\mathbb{E}[\bm{x}\mid\bm{y}]$ , given various information about the model and (potentially finite) samples of either $\bm{x}$ or $\bm{y}$ .

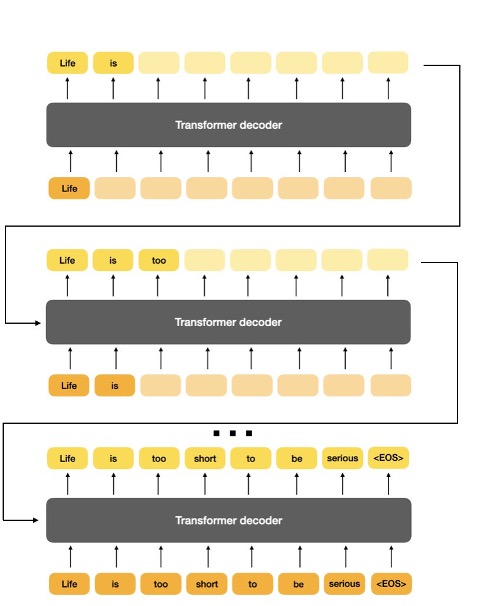
Example 6.1 (Image Completion and Text Prediction).

The popular natural image completion and natural language prediction are two typical tasks that require us to recover a full data $\bm{x}$ from its partial observations $\bm{y}$ , with parts of $\bm{x}$ masked out and to be completed based on the rest. Figure 6.2 shows some examples of such tasks. In fact, it is precisely these tasks which have inspired how to train modern large models for text generation (such as GPT) and image completion (such as the masked autoencoder) that we will study in greater details later.

Figure 6.2 : Left: image completion. Right: text prediction. In particular, text prediction is the inspiration for the popular Generative Pre-trained Transformer (GPT). — Figure 6.2: Left: image completion. Right: text prediction. In particular, text prediction is the inspiration for the popular Generative Pre-trained Transformer (GPT).

$\blacksquare$

Statistical interpretation via Bayes’ rule.

Generally speaking, to accomplish such tasks well, we need to get ahold of the conditional distribution $p(\bm{x}\mid\bm{y})$ . If we had this, then we would be able to find the maximal likelihood estimate (prediction):

\hat{\bm{x}}=\operatorname*{arg\ max}_{\bm{x}}p(\bm{x}\mid\bm{y});

(6.1.2)

compute the conditional expectation estimate:

\hat{\bm{x}}=\mathbb{E}[\bm{x}\mid\bm{y}]=\int\bm{x}p(\bm{x}\mid\bm{y})\mathrm{d}\bm{x};

(6.1.3)

and sample from the conditional distribution:

\hat{\bm{x}}\sim p(\bm{x}\mid\bm{y}).

(6.1.4)

Notice that from Bayes’ rule, we have

p(\bm{x}\mid\bm{y})=\frac{p(\bm{y}\mid\bm{x})p(\bm{x})}{p(\bm{y})}.

(6.1.5)

For instance, the maximal likelihood estimate can be computed by solving the following (maximal log likelihood) program:

\hat{\bm{x}}=\operatorname*{arg\ max}_{\bm{x}}[\log p(\bm{y}\mid\bm{x})+\log p(\bm{x})],

(6.1.6)

say via gradient ascent:

\bm{x}_{k+1}=\bm{x}_{k}+\alpha\cdot\big{(}\nabla_{\bm{x}}\log p(\bm{y}\mid\bm{x})+\nabla_{\bm{x}}\log p(\bm{x})\big{)}.

(6.1.7)

Efficiently computing the conditional distribution $p(\bm{x}\mid\bm{y})$ naturally depends on how we learn and exploit the low-dimensional distribution $p(\bm{x})$ of the data $\bm{x}$ and the observation model $\bm{y}=h(\bm{x})+\bm{w}$ that determines the conditional distribution $p(\bm{y}\mid\bm{x})$ .

Remark 6.1 (End-to-End versus Bayesian).

In the modern practice of data-driven machine learning, for certain popular tasks people often directly learn the conditional distribution $p(\bm{x}\mid\bm{y})$ or a (probabilistic) mapping or a regressor. Such a mapping is often modeled by some deep networks and trained end-to-end with sufficient paired samples $(\bm{x},\bm{y})$ . Such an approach is very different from the above Bayesian approach in which both the distribution of $\bm{x}\sim p(\bm{x})$ and the (observation) mapping are needed. The benefit of the Bayesian approach is that the learned distribution $p(\bm{x})$ can facilitate many different tasks with varied observation models and conditions.

Geometric interpretation as constrained optimization.

As the support $\mathcal{S}_{\bm{x}}$ of the distribution of $\bm{x}$ is low-dimensional, we may assume that there exists a function $F$ such that

F(\bm{x})=\bm{0}\qquad\iff\qquad\bm{x}\in\mathcal{S}_{\bm{x}}

(6.1.8)

such that $\mathcal{S}_{\bm{x}}=F^{-1}(\{\bm{0}\})$ is the low-dimensional support of the distribution $p(\bm{x})$ . Geometrically, one natural choice of $F(\bm{x})$ is the “distance function” to the support $\mathcal{S}_{\bm{x}}$ :¹¹1Notice that, in reality, we only have discrete samples on the support of the distribution. In the same spirit of continuation, through diffusion or lossy coding studied in Chapter 3, we may approximate the distance function as $F(\bm{x})\approx\min_{\bm{x}_{p}\in\mathcal{C}_{\bm{x}}^{\epsilon}}\|\bm{x}-\bm{x}_{p}\|_{2}$ where $\mathcal{S}_{\bm{x}}$ is replaced by a covering $\mathcal{C}_{\bm{x}}^{\epsilon}$ of the samples with $\epsilon$ -balls.

F(\bm{x})=\min_{\bm{x}_{p}\in\mathcal{S}_{\bm{x}}}\|\bm{x}-\bm{x}_{p}\|_{2}.

(6.1.9)

Now given $\bm{y}=h(\bm{x})+\bm{w}$ , to solve for $\bm{x}$ , we can solve the following constrained optimization problem:

\max_{\bm{x}}-\frac{1}{2}\|h(\bm{x})-\bm{y}\|_{2}^{2}\quad\mbox{s.t.}\quad F(\bm{x})=\bm{0}.

(6.1.10)

Using the method of augmented Lagrange multipliers, we can solve the following unconstrained program:

\max_{\bm{x}}\left[-\frac{1}{2}\|h(\bm{x})-\bm{y}\|_{2}^{2}+\bm{\lambda}^{\top}F(\bm{x})-\frac{\mu}{2}\|F(\bm{x})\|_{2}^{2}\right]

(6.1.11)

for some constant Lagrange multipliers $\bm{\lambda}$ . This is equivalent to the following program:

\max_{\bm{x}}\left[\log\exp\Big{(}-\frac{1}{2}\|h(\bm{x})-\bm{y}\|_{2}^{2}\Big{)}+\log\exp\Big{(}-\frac{\mu}{2}\big{\|}F(\bm{x})-\bm{\lambda}/\mu\big{\|}_{2}^{2}\Big{)}\right],

(6.1.12)

where $\bm{c}\doteq{\bm{\lambda}}/{\mu}$ can be viewed as a “mean” for the constraint function. As $\mu$ becomes large when enforcing the constraint via continuation²²2In the same spirit of continuation in Chapter 3 where we obtained better approximations of our distribution by sending $\varepsilon\to 0$ , here we send $\mu\to\infty$ . Larger values of $\mu$ will constrain $F$ to take smaller and smaller values at the optimum, meaning that the optimum lies within a smaller and smaller neighborhood of the support $\mathcal{S}_{\bm{x}}$ . Interestingly, the theory of Lagrange multipliers hints that, under certain benign conditions on $F$ and other terms in the objective, we only need to make $\mu$ large enough in order to ensure $F(\bm{x})=\bm{0}$ at the optimum, meaning that at finite penalty we get perfect approximation of the support. In general, we should have the intuition that $\mu$ plays the same role as $\epsilon^{-1}$ ., $\|\bm{c}\|_{2}$ becomes increasingly small.

The above program may be interpreted in two different ways. Firstly, one may view the first term as the conditional probability of $\bm{y}$ given $\bm{x}$ , and the second term as a probability density for $\bm{x}$ :

p(\bm{y}\mid\bm{x})\propto\exp\Big{(}-\frac{1}{2}\|h(\bm{x})-\bm{y}\|_{2}^{2}\Big{)},\quad p(\bm{x})\propto\exp\Big{(}-\frac{\mu}{2}\|F(\bm{x})-\bm{c}\|_{2}^{2}\Big{)}.

(6.1.13)

Hence, solving the constrained optimization for the inverse problem is equivalent to conducting Bayes inference with the above probability densities. Hence solving the above program (6.1.12) via gradient ascent is equivalent to the above maximal likelihood estimate (6.1.7), in which the gradient takes the form:

\nabla_{\bm{x}}\log p(\bm{y}\mid\bm{x})+\nabla_{\bm{x}}\log p(\bm{x})=\frac{\partial h}{\partial\bm{x}}(\bm{x})\big{(}\bm{y}-h(\bm{x})\big{)}+\mu\frac{\partial F}{\partial\bm{x}}(\bm{x})\big{(}\bm{c}-F(\bm{x})\big{)},

(6.1.14)

where $\frac{\partial h}{\partial\bm{x}}(\bm{x})$ and $\frac{\partial F}{\partial\bm{x}}(\bm{x})$ are the Jacobians of $h(\bm{x})$ and $F(\bm{x})$ , respectively.

Secondly, notice that the above program (6.1.12) is equivalent to:

\min_{\bm{x}}\frac{1}{2}\|h(\bm{x})-\bm{y}\|_{2}^{2}+\frac{\mu}{2}\big{\|}F(\bm{x})-\bm{\lambda}/\mu\big{\|}_{2}^{2},

(6.1.15)

Due to the conspicuous quadratic form of the two terms, they can also be interpreted as certain “energy” functions. Such a formulation is often referred to as “Energy Minimization” in the machine learning literature.

Several representative practical settings for inference.

In practice, however, initial information about the distributions of $\bm{x}$ and the relationship between $\bm{x}$ and $\bm{y}$ can be given in many different ways and forms. In general, they can mostly be categorized into four cases, which are, conceptually, increasingly more challenging:

•

Case 1: Both a model for the distribution of $\bm{x}$ and the observation model $\bm{y}=h(\bm{x})$ $(+\bm{w})$ are known, even with an analytical form. This is typically the case for many classic signal processing problems, such as signal denoising, the sparse vector recovery problem we saw in Chapter 2 and the low-rank matrix recovery problem to be introduced below.
•

Case 2: We do not have a model for the distribution but only samples $\bm{X}=\{\bm{x}_{1},\ldots,\bm{x}_{N}\}$ of $\bm{x}$ , and the observation model $\bm{y}=h(\bm{x})$ $(+\bm{w})$ is known.³³3In the literature, this setting is sometimes referred to as the empirical Bayesian inference. A model for the distribution $p(\bm{x})$ of $\bm{x}$ needs to be learned, and subsequently the conditional distribution $p(\bm{x}\mid\bm{y})$ . Natural image completion or natural language completion (e.g., BERT and GPT) are typical examples of this class of problems.
•

Case 3: We only have the paired samples: $(\bm{X},\bm{Y})=\{(\bm{x}_{1},\bm{y}_{1}),\ldots,(\bm{x}_{N},\bm{y}_{N})\}$ of the two variables $(\bm{x},\bm{y})$ . The distributions of $\bm{x}$ and $\bm{y}$ and their relationship $h(\cdot)$ need to be learned from these paired sample data. For example, given many images and their captions, learning to conduct text-conditioned image generation is one such problem.
•

Case 4: We only have the samples $\bm{Y}=\{\bm{y}_{1},\ldots,\bm{y}_{N}\}$ of the observations $\bm{y}$ , and the observation model $h(\cdot)$ needs to be known, at least in some parametric family $h(\cdot,\bm{\theta})$ . The distribution $p(\bm{x})$ and $p(\bm{x}\mid\bm{y})$ need to be learned from $\hat{\bm{x}}$ , estimated from $\bm{Y}$ . For example, learning to render a new view from a sequence of calibrated or uncalibrated views is one such problem.

In this chapter, we will discuss general approaches to learn the desired distributions and solve the associated conditional estimation or generation for these cases, typically with a representative problem. Throughout the chapter, you should keep Figure 6.1 in mind.

6.2 Conditional Inference with a Known Data Distribution

Notice that in the setting we have discussed in previous Chapters, the autoencoding network is trained to reconstruct a set of samples of the random vector $\bm{x}$ . This would allow us to regenerate samples from the learned (low-dimensional) distribution. In practice, the low-dimensionality of the distribution, once given or learned, can be exploited for stable and robust recovery, completion, or prediction tasks. That is, under rather mild conditions, one can recover $\bm{x}$ from highly compressive, partial, noisy or even corrupted measures of $\bm{x}$ of the kind:

\bm{y}=h(\bm{x})+\bm{w},

(6.2.1)

where $\bm{y}$ is typically an observation of $\bm{x}$ that is of much lower dimension than $\bm{x}$ and $\bm{w}$ can be random noise or even sparse gross corruptions. This is a class of problems that have been extensively studied in the classical signal processing literature, for low-dimensional structures such as sparse vectors, low-rank matrices, and beyond. Interested readers may see [WM22] for a complete exposition of this topic.

Here to put the classic work in a more general modern setting, we illustrate the basic idea and facts through the arguably simplest task of data (and particularly image) completion. That is, we consider the problem of recovering a sample $\bm{x}$ when parts of it are missing (or even corrupted). We want to recover or predict the rest of $\bm{x}$ from observing only a fraction of it:

f:\mathcal{P}_{\Omega}(\bm{x})\mapsto\hat{\bm{x}},

(6.2.2)

where $\mathcal{P}_{\Omega}(\,\cdot\,)$ represents a masking operation (see Figure 6.3 for an example).

In this section and the next, we will study the completion task under two different scenarios: One is when the distribution of the data $\bm{x}$ of interest is already given apriori, even in a certain analytical form. This is the case that prevails in classic signal processing where the structures of the signals are assumed to be known, for example, band-limited, sparse or low-rank. The other is when only raw samples of $\bm{x}$ are available and we need to learn the low-dimensional distribution from the samples in order to solve the completion task well. This is the case for the tasks of natural image completion or video frame prediction. As a precursor to the rest of the chapter, we start with the simplest case of image completion: when the image to be completed can be well modeled as a low-rank matrix. We will move on to increasingly more general cases and more challenging settings later.

Low-rank matrix completion.

The low-rank matrix completion problem is a classical problem for data completion when its distribution is low-dimensional and known. Consider a random sample of a matrix $\bm{X}_{o}=[\bm{x}_{1},\ldots,\bm{x}_{n}]\in\mathbb{R}^{m\times n}$ from the space of all matrices of rank $r$ . In general, we assume the rank of the matrix is

\mbox{rank}(\bm{X}_{o})=r<\min\{m,n\}.

(6.2.3)

So it is clear that locally the intrinsic dimension of the space of all matrices of rank $r$ is much lower than the ambient space $mn$ .

Now, let $\Omega$ indicate a set of indices of observed entries of the matrix $\bm{X}_{o}$ . Let the observed entries be:

\bm{Y}=\mathcal{P}_{\Omega}(\bm{X}_{o}).

(6.2.4)

The remaining entries supported on $\Omega^{c}$ are unobserved or missing. The problem is whether we can recover from $\bm{Y}$ the missing entries of $\bm{X}$ correctly and efficiently. Figure 6.3 shows one example of completing such a matrix.

Figure 6.3 : Illustration of completing an image as low-rank matrix with some entries masked or corrupted. Left: the masked/corrupted image 𝒀 \bm{Y} bold_italic_Y ; middle: the mask Ω \Omega roman_Ω ; right: the completed image 𝑿 ^ \hat{\bm{X}} over^ start_ARG bold_italic_X end_ARG . — Figure 6.3: Illustration of completing an image as low-rank matrix with some entries masked or corrupted. Left: the masked/corrupted image $\bm{Y}$ ; middle: the mask $\Omega$ ; right: the completed image $\hat{\bm{X}}$ .

Notice that the fundamental reason why such a matrix can be completed is that columns and rows of the matrix are highly correlated and they all lie on a low-dimensional subspace. For the example shown in Figure 6.3, the dimension or the rank of the matrix completed is only two. Hence the fundamental idea to recover such a matrix is to seek a matrix that has the lowest rank among all matrices that have entries agreeing with the observed ones:

\min_{\bm{X}}\mbox{rank}(\bm{X})\quad\mbox{subject to}\quad\bm{Y}=\mathcal{P}_{\Omega}(\bm{X}).

(6.2.5)

This is known as the low-rank matrix completion problem. See [WM22] for a full characterization of the space of all low-rank matrices. As the rank function is discontinuous and rank minimization is in general an NP-hard problem, we would like to relax it with something easier to optimize.

Based on our knowledge about compression from Chapter 3, we could promote the low-rankness of the recovered matrix $\bm{X}$ by enforcing the lossy coding rate (or the volume spanned by $\bm{X}$ ) of the data in $\bm{X}$ to be small:

\min R_{\epsilon}(\bm{X})=\frac{1}{2}\log\det\left(\bm{I}+\alpha\bm{X}\bm{X}^{\top}\right)\quad\mbox{subject to}\quad\bm{Y}=\mathcal{P}_{\Omega}(\bm{X}).

(6.2.6)

The problem can viewed as a continuous relaxation of the above low-rank matrix completion problem (6.2.5) and it can be solved via gradient descent. One can show that the gradient descent operator for the $\log\det$ objective is precisely minimizing a close surrogate of the rank of the matrix $\bm{X}\bm{X}^{\top}$ .

The rate distortion function is a nonconvex function, and its gradient descent does not always guarantee finding the globally optimal solution. Nevertheless, since the underlying structure sought for $\bm{X}$ is piecewise linear, the rank function admits a rather effective convex relaxation: the nuclear norm—the sum of all singular values of the matrix $\bm{X}$ . As shown in the compressive sensing literature, under fairly broad conditions,⁴⁴4Typically, such conditions specify the necessary and sufficient amount of entries needed for the completion to be computationally feasible. These conditions have been systematically characterized in [WM22]. the matrix completion problem (6.2.5) can be effectively solved by the following convex program:

\min\|\bm{X}\|_{*}\quad\mbox{subject to}\quad\bm{Y}=\mathcal{P}_{\Omega}(\bm{X}),

(6.2.7)

where the nuclear norm $\|\bm{X}\|_{*}$ is the sum of singular values of $\bm{X}$ . In practice, we often convert the above constrained convex optimization program to an unconstrained one:

\min\|\bm{X}\|_{*}+\lambda\|\bm{Y}-\mathcal{P}_{\Omega}(\bm{X})\|_{F}^{2},

(6.2.8)

for some properly chosen $\lambda>0$ . Interested readers may refer to [WM22] for how to develop algorithms that can solve the above programs efficiently and effectively. Figure 6.3 shows a real example in which the matrix $\hat{\bm{X}}$ is actually recovered by solving the above program.

Further extensions.

It has been shown that images (or more accurately textures) and 3D scenes with low-rank structures can be very effectively completed via solving optimization programs of the above kind, even if there is additional corruption and distortion [ZLG+10, LRZ+12, YZB+23]:

\bm{Y}\circ\tau=\bm{X}_{o}+\bm{E},

(6.2.9)

where $\tau$ is some unknown nonlinear distortion of the image and $\bm{E}$ is an unknown matrix that models some (sparse) occlusion and corruption. Again, interested readers may refer to [WM22] for a more detailed account.

6.3 Conditional Inference with a Learned Data Representation

In the previous subsection, the reason we can infer $\bm{x}$ from the partial observation $\bm{y}$ is because (support of) the distribution of $\bm{X}$ is known or specified apriori, say as the set of all low-rank matrices. For many practical datasets, we do not have their distribution in an analytical form like the low-rank matrices, say the set of all natural images. Nevertheless, if we have sufficient samples of the data $\bm{x}$ , we should be able to learn its low-dimensional distribution first and leverage it for future inference tasks based on an observation $\bm{y}=h(\bm{x})+\bm{w}$ . In this section, we assume the observation model $h(\cdot)$ is given and known. We will study the case when $h(\cdot)$ is not explicitly given in the next section.

6.3.1 Image Completion with Masked Auto-Encoding

For a general image $\bm{X}$ such as the one shown on the left of Figure 6.4, we can no longer view it as a low-rank matrix. However, humans still demonstrate remarkable ability to complete a scene and recognize familiar objects despite severe occlusion. This suggests that our brain has learned the low-dimensional distribution of natural images and can use it for completion, and hence recognition. However, the distribution of all natural images is not as simple as a low-dimensional linear subspace. Hence a natural question is whether we can learn the more sophisticated distribution of natural images and use it to perform image completion?

Figure 6.4 : Diagram of the overall (masked) autoencoding process. The (image) token representations are transformed iteratively towards a parsimonious (e.g., compressed and sparse) representation by each encoder layer f ℓ f^{\ell} italic_f start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT . Furthermore, such representations are transformed back to the original image by the decoder layers g ℓ g^{\ell} italic_g start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT . Each encoder layer f ℓ f^{\ell} italic_f start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT is meant to be (partially) inverted by a corresponding decoder layer g L − ℓ g^{L-\ell} italic_g start_POSTSUPERSCRIPT italic_L - roman_ℓ end_POSTSUPERSCRIPT . — Figure 6.4: Diagram of the overall (masked) autoencoding process. The (image) token representations are transformed iteratively towards a parsimonious (e.g., compressed and sparse) representation by each encoder layer $f^{\ell}$ . Furthermore, such representations are transformed back to the original image by the decoder layers $g^{\ell}$ . Each encoder layer $f^{\ell}$ is meant to be (partially) inverted by a corresponding decoder layer $g^{L-\ell}$ .

One empirical approach to the image completion task is to find an encoding and decoding scheme by solving the following masked autoencoding (MAE) program that minimizes the reconstruction loss:

\min_{f,g}L_{\mathrm{MAE}}(f,g)\doteq\mathbb{E}\big{[}\|(g\circ f)(\mathcal{P}_{\Omega}(\bm{X}))-\bm{X}\|_{2}^{2}].

(6.3.1)

Unlike the matrix completion problem which has a simple underlying structure, we should no longer expect that the encoding and decoding mappings admit simple closed forms or the program can be solved by explicit algorithms.

For a general natural image, we can no longer assume that its columns or rows are sampled from a low-dimensional subspace or a low-rank Gaussian. However, it is reasonable to assume that the image consists of multiple regions. Image patches in each region are similar and can be modeled as one (low-rank) Gaussian or subspace. Hence, to exploit the low-dimensionality of the distribution, the objective of the encoder $f$ is to transform $\bm{X}$ to a representation $\bm{Z}$ :

f:\bm{X}\mapsto\bm{Z}

(6.3.2)

such that the distribution of $\bm{Z}$ can be well modeled as a mixture of subspaces, say $\{\bm{U}_{[K]}\}$ , such that the rate reduction is maximized while the sparsity is minimized:

\mathbb{E}_{\bm{Z}=f(\bm{X})}[\Delta R_{\epsilon}(\bm{Z}\mid\bm{U}_{[K]})-\lambda\|\bm{Z}\|_{0}]=\mathbb{E}_{\bm{Z}=f(\bm{X})}[R_{\epsilon}(\bm{Z})-R^{c}_{\epsilon}(\bm{Z}\mid\bm{U}_{[K]})-\lambda\|\bm{Z}\|_{0}],

(6.3.3)

where the functions $R_{\epsilon}(\cdot)$ and $R^{c}_{\epsilon}(\cdot)$ are defined in (4.2.2) and (4.2.3), respectively.

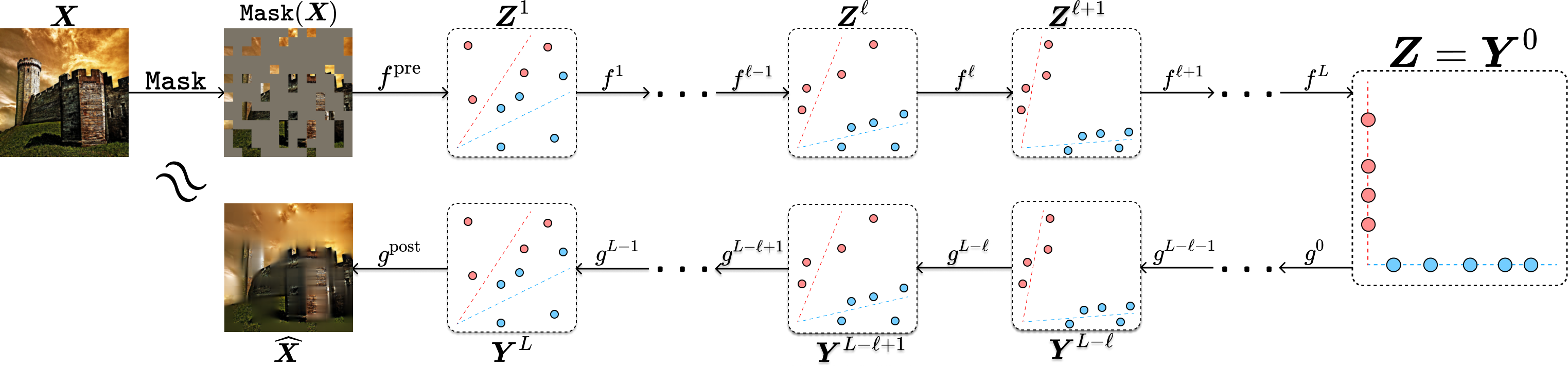
As we have shown in the previous Chapter 4, the encoder $f$ that minimizes the above objective can be constructed as a sequence of transformer-like operators. As shown in the work of [PBW+24], the decoder $g$ can be viewed and hence constructed explicitly as the inverse process of the encoder $f$ . Figure 6.5 illustrates the overall architectures of both the encoder and the corresponding decoder at each layer. The parameters of the encoder $f$ and decoder $g$ can be learned by optimizing the reconstruction loss (6.3.1) via gradient descent.

Figure 6.5 : Diagram of each encoder layer ( top ) and decoder layer ( bottom ). Notice that the two layers are highly anti-parallel — each is constructed to do the operations of the other in reverse order. That is, in the decoder layer g ℓ g^{\ell} italic_g start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT , the ISTA \operatorname{ISTA} roman_ISTA block of f L − ℓ f^{L-\ell} italic_f start_POSTSUPERSCRIPT italic_L - roman_ℓ end_POSTSUPERSCRIPT is partially inverted first using a linear layer, then the MSSA \operatorname{MSSA} roman_MSSA block of f L − ℓ f^{L-\ell} italic_f start_POSTSUPERSCRIPT italic_L - roman_ℓ end_POSTSUPERSCRIPT is reversed; this order unravels the transformation done in f L − ℓ f^{L-\ell} italic_f start_POSTSUPERSCRIPT italic_L - roman_ℓ end_POSTSUPERSCRIPT . — Figure 6.5: Diagram of each encoder layer (top) and decoder layer (bottom). Notice that the two layers are highly anti-parallel — each is constructed to do the operations of the other in reverse order. That is, in the decoder layer $g^{\ell}$ , the $\operatorname{ISTA}$ block of $f^{L-\ell}$ is partially inverted first using a linear layer, then the $\operatorname{MSSA}$ block of $f^{L-\ell}$ is reversed; this order unravels the transformation done in $f^{L-\ell}$ .

Figure 6.6 shows some representative results of the thus-designed masked auto-encoder. More implementation details and results of the masked autoencoder for natural image completion can be found in Chapter 7.

Figure 6.6 : Autoencoding visualizations of CRATE-Base and ViT-MAE-Base [ HCX+22 ] with 75% patches masked. We observe that the reconstructions from CRATE-Base are on par with the reconstructions from ViT-MAE-Base, despite using < 1 / 3 <1/3 < 1 / 3 of the parameters. — Figure 6.6: Autoencoding visualizations of CRATE-Base and ViT-MAE-Base [HCX+22] with 75% patches masked. We observe that the reconstructions from CRATE-Base are on par with the reconstructions from ViT-MAE-Base, despite using $<1/3$ of the parameters.

6.3.2 Conditional Sampling with Measurement Matching

The above (masked) autoencoding problem aims to generate a sample image that is consistent with certain observations or conditions. But let us examine the approach more closely: given the visual part of an image $\bm{X}_{v}=\mathcal{P}_{\Omega}(\bm{X})$ , we try to estimate the masked part $\bm{X}_{m}=\mathcal{P}_{\Omega^{c}}(\bm{X})$ . For realizations $(\bm{\Xi}_{v},\bm{\Xi}_{m})$ of the random variable $\bm{X}=(\bm{X}_{v},\bm{X}_{m})$ , let

p_{\bm{X}_{m}\mid\bm{X}_{v}}(\bm{\Xi}_{m}\mid\bm{\Xi}_{v})

be the conditional distribution of $\bm{X}_{m}$ given $\bm{X}_{v}$ . It is easy to show that the optimal solution to the MAE formulation (6.3.1) is given by the conditional expectation:

\operatorname*{arg\ min}_{h=g\circ f}\,L_{\mathrm{MAE}}(h)=\bm{\Xi}_{v}\mapsto\bm{\Xi}_{v}+\mathbb{E}[\bm{X}_{m}\mid\bm{X}_{v}=\bm{\Xi}_{v}].

(6.3.4)

In general, however, this expectation may not even lie on the low-dimensional distribution of natural images! This partially explains why some of the recovered patches in Figure 6.6 are a little blurry.

For many practical purposes, we would like to learn (a representation of) the conditional distribution $p_{\bm{X}_{m}\mid\bm{X}_{v}}$ , or equivalently $p_{\bm{X}\mid\bm{X}_{v}}$ , and then get a clear (most likely) sample from this distribution directly. Notice that, when the distribution of $\bm{X}$ is low-dimensional, it is possible that if a sufficient part of $\bm{X}$ , $\bm{X}_{v}$ , is observed, it fully determines $\bm{X}$ and hence the missing part $\bm{X}_{m}$ . In other words, the distribution $p_{\bm{X}\mid\bm{X}_{v}}$ is a generalized function—if $\bm{X}$ is fully determined by $\bm{X}_{v}$ it is the delta function, and more generally one of its exotic cousins.

Hence, instead of solving the completion task as a conditional estimation problem, we should address it as a conditional sampling problem. To that end, we should first learn the (low-dimensional) distribution of all natural images $\bm{X}$ . If we have sufficient samples of natural images, we can learn the distribution via a denoising process $\bm{X}_{t}$ described in Chapter 3. Then the problem of recovering $\bm{X}$ from its partial observation $\bm{Y}=\mathcal{P}_{\Omega}(\bm{x})+\bm{w}$ becomes a conditional generation problem – to sample the distribution conditioned on the observation.

Figure 6.7 : Sampling visualizations from models trained via ambient diffusion [ DSD+23a ] with 80% of the pixels masked. Using a similar ratio of masked pixels as in Figure 6.6 , the ambient diffusion sampling algorithm recovers a much sharper image than the blurry image recovered by the MAE-based method. The former method samples from the distribution of natural images, while the latter approximates the conditional expectation (i.e., average) of this distribution given the observation; this averaging causes the blurriness. — Figure 6.7: Sampling visualizations from models trained via ambient diffusion [DSD+23a] with 80% of the pixels masked. Using a similar ratio of masked pixels as in Figure 6.6, the ambient diffusion sampling algorithm recovers a much sharper image than the blurry image recovered by the MAE-based method. The former method samples from the distribution of natural images, while the latter approximates the conditional expectation (i.e., average) of this distribution given the observation; this averaging causes the blurriness.

General linear measurements.

In fact, we may even consider recovering $\bm{X}$ from a more general linear observation model:

\bm{Y}=\bm{A}\bm{X}_{0},\quad\bm{X}_{t}=\bm{X}_{0}+\sigma_{t}\bm{G},

(6.3.5)

where $\bm{A}$ is a linear operator on matrix space⁵⁵5i.e., if we imagine unrolling $\bm{X}$ into a long vector then $\bm{A}$ takes the role of a matrix on $\bm{X}$ -space and $\bm{G}\sim\mathcal{N}(\bm{0},\bm{I})$ . The masking operator $\mathcal{P}_{\Omega}(\cdot)$ in the image completion task is one example of such a linear model. Then it has been shown by [DSD+23] that

\hat{\bm{X}}_{*}=\operatorname*{arg\ min}_{\hat{\bm{X}}}\mathbb{E}[\|\bm{A}(\hat{\bm{X}}(\bm{A}\bm{X}_{t},\bm{A})-\bm{X}_{0})\|^{2}]

(6.3.6)

satisfies the condition that:

\bm{A}\hat{\bm{X}}_{*}(\bm{A}(\bm{X}_{t}),\bm{A})=\bm{A}\mathbb{E}[\bm{X}_{0}\mid\bm{A}\bm{X}_{t},\bm{A}].

(6.3.7)

Notice that in the special case when $\bm{A}$ is of full column rank, we have $\mathbb{E}[\bm{X}_{0}\mid\bm{A}\bm{X}_{t},\bm{A}]=\mathbb{E}[\bm{X}_{0}\mid\bm{X}_{t}]$ . Hence, in the more general case, it has been suggested by [DSD+23] that one could still use the so obtained $\mathbb{E}[\bm{X}_{0}\mid\bm{A}(\bm{X}_{t}),\bm{A}]$ to replace the $\mathbb{E}[\bm{X}_{0}\mid\bm{X}_{t}]$ in the normal denoising process for $\bm{X}_{t}$ :

\bm{X}_{t-s}=\gamma_{t}\bm{X}_{t}+(1-\gamma_{t})\mathbb{E}[\bm{X}_{0}\mid\bm{A}\bm{X}_{t},\bm{A}].

(6.3.8)

This usually works very well in practice, say for many image restoration tasks, as shown in [DSD+23]. Compared to the blurry images recovered from MAE, the images recovered by the above method are much sharper as it leverages a learned distribution of natural images and samples a (sharp) image from the distribution that is consistent with the measurement, as shown in Figure 6.7 (cf Figure 6.6).

General nonlinear measurements.

To generalize the above (image) completion problems and make things more rigorous, we may consider that a random vector $\bm{x}\sim p$ is partially observed through a more general observation function:

\bm{y}=h(\bm{x})+\bm{w},

(6.3.9)

where $\bm{w}$ usually stands for some random measurement noise, say of a Gaussian distribution $\bm{w}\sim\mathcal{N}(\mathbf{0},\sigma^{2}\bm{I})$ . It is easy to see that, for $\bm{x}$ and $\bm{y}$ so related, their joint distribution $p(\bm{x},\bm{y})$ is naturally nearly degenerate if the noise $\bm{w}$ is small. To a large extent, we may view $p(\bm{x},\bm{y})$ as a noisy version of a hypersurface defined by the function $\bm{y}=h(\bm{x})$ in the joint space $(\bm{x},\bm{y})$ . Practically speaking, we will consider a setting more akin to masked autoencoding than to pure matrix completion, where we always have access to a corresponding clean sample $\bm{x}$ for every observation $\bm{y}$ we receive.⁶⁶6In some more specialized applications, in particular in scientific imaging, it is of interest to be able to learn to generate samples from the posterior $p_{\bm{x}\mid\bm{y}}$ without access to any clean/ground-truth samples of $\bm{x}$ . We give a brief overview of methods for this setting in the end-of-chapter notes.

Like image/matrix completion, we are often faced with a setting where $\bm{y}$ denotes a degraded or otherwise “lossy” observation of the input $\bm{x}$ . This can manifest in quite different forms. For example, in various scientific or medical imaging problems, the measured data $\bm{y}$ may be a compressed and corrupted observation of the underlying data $\bm{x}$ ; whereas in 3D vision tasks, $\bm{y}$ may represent an image captured by a camera of a physical object with an unknown (low-dimensional) pose $\bm{x}$ . Generally, by virtue of mathematical modeling (and, in some cases, co-design of the measurement system), we know $h$ and can evaluate it on any input, and we can exploit this knowledge to help reconstruct and sample $\bm{x}$ .

(a)

(b)

Figure 6.8: Statistical dependency diagrams for the conditional sampling process. Left: In a direct (conceptual) application of the diffusion-denoising scheme we have developed in Chapter 3 to conditional sampling, we use samples from the posterior

p_{\bm{x}\mid\bm{y}}

to train denoisers directly on the posterior at different noise levels, then use them to generate new samples. In practice, however, we do not normally have direct samples from the posterior, but rather paired samples

(\bm{x},\bm{y})

from the joint. Right: It turns out that it suffices to have only noisy observations of

\bm{x}

to realize the denoisers corresponding to

p_{\bm{x}^{\mathrm{c}}_{t}\mid\bm{x}^{\mathrm{c}}}

: this follows from conditional independence of

\bm{x}_{t}

and

\bm{y}

given

\bm{x}

. It implies that

p_{\bm{x}^{\mathrm{c}}_{t}}=p_{\bm{x}_{t}\mid\bm{y}}

, which gives a score function for denoising that consists of the unconditional score function, plus a correction term that enforces measurement consistency.

At a technical level, we want the learned representation of the data to facilitate us to sample the conditional distribution $p_{\bm{x}\mid\bm{y}}$ , also known as the posterior, effectively and efficiently. More precisely, write $\bm{\nu}$ to denote a realization of the random variable $\bm{y}$ . We want to generate samples $\hat{\bm{x}}$ such that:

\hat{\bm{x}}\sim p_{\bm{x}\mid\bm{y}}(\,\cdot\,\mid\bm{y}=\bm{\nu}).

(6.3.10)

Recall that in Section 3.2, we have developed a natural and effective way to produce unconditional samples of the data distribution $p$ . The ingredients are the denoisers $\bar{\bm{x}}^{\ast}(t,\bm{\xi})=\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]$ , or their learned approximations $\bar{\bm{x}}_{\theta}(t,\bm{\xi})$ , for different levels of noisy observations $\bm{x}_{t}=\bm{x}+t\bm{g}$ (and $\bm{\xi}$ for their realizations) under Gaussian noise $\bm{g}\sim\mathcal{N}(\mathbf{0},\bm{I})$ , and $t\in[0,T]$ with a choice of times $0=t_{1}<\ldots<t_{L}=T$ at which to perform the iterative denoising, starting from $\hat{\bm{x}}_{t_{L}}\sim\mathcal{N}(\mathbf{0},T^{2}\bm{I})$ (recall Equation 3.2.66).⁷⁷7Recall from our discussion in Section 3.2.2 that a few small improvements to this basic iterative denoising scheme are sufficient to bring competitive practical performance. For clarity as we develop conditional sampling, we will focus here on the simplest instantiation. We could directly apply this scheme to generate samples from the posterior $p_{\bm{x}\mid\bm{y}}$ if we had access to a dataset of samples $\bm{x}^{\mathrm{c}}\sim p_{\bm{x}\mid\bm{y}}(\,\cdot\,\mid\bm{\nu})$ for each realization $\bm{\nu}$ of $\bm{y}$ , by generating noisy observations $\bm{x}^{\mathrm{c}}_{t}$ and training denoisers to approximate $\mathbb{E}[\bm{x}^{\mathrm{c}}\mid\bm{x}^{\mathrm{c}}_{t}=\,\cdot\,,\bm{y}=\bm{\nu}]$ , the mean of the posterior under the noisy observation (see Figure 6.8(a)). However, performing this resampling given only paired samples $(\bm{x},\bm{y})$ from the joint distribution (say by binning the samples over values of $\bm{y}$ ) requires prohibitively many samples for high-dimensional data, and alternate approaches explicitly or implicitly rely on density estimation, which similarly suffers from the curse of dimensionality.

Fortunately, it turns out that this is not necessary. Consider the alternate statistical dependency diagram in Figure 6.8(b), which corresponds to the random variables in the usual denoising-diffusion process, together with the measurement $\bm{y}$ . Because our assumed observation model (6.3.9) implies that $\bm{x}_{t}$ and $\bm{y}$ are independent conditioned on $\bm{x}$ , we have for any realization $\bm{\nu}$ of $\bm{y}$

\begin{split}p_{\bm{x}^{\mathrm{c}}_{t}\mid\bm{y}}(\,\cdot\,\mid\bm{\nu})&=\int\underbrace{p_{\bm{x}^{\mathrm{c}}_{t}\mid\bm{x}^{\mathrm{c}}}(\,\cdot\,\mid\bm{\xi})}_{=\mathcal{N}(\bm{\xi},t^{2}\bm{I})}\,\cdot\,\underbrace{p_{\bm{x}^{\mathrm{c}}\mid\bm{y}}}_{=p_{\bm{x}\mid\bm{y}}}(\bm{\xi}\mid\bm{\nu})\mathrm{d}\bm{\xi}\\ &=\int p_{\bm{x}_{t}\mid\bm{x},\bm{y}}(\,\cdot\,\mid\bm{\xi},\bm{\nu})\,\cdot\,p_{\bm{x}\mid\bm{y}}(\bm{\xi}\mid\bm{\nu})\mathrm{d}\bm{\xi}\\ &=\int p_{\bm{x}_{t},\bm{x}\mid\bm{y}}(\,\cdot\,,\bm{\xi}\mid\bm{\nu})\mathrm{d}\bm{\xi}\\ &=p_{\bm{x}_{t}\mid\bm{y}}(\,\cdot\,\mid\bm{\nu}).\end{split}

(6.3.11)

Above, the first line recognizes an equivalence between the distributions arising in Figure 6.8 (a,b); the second line applies this together with conditional independence of $\bm{x}_{t}$ and $\bm{y}$ given $\bm{x}$ ; the third line uses the definition of conditional probability; and the final line marginalizes over $\bm{x}$ . Thus, the denoisers from the conceptual posterior sampling process are equal to $\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\,\cdot\,,\bm{y}=\bm{\nu}]$ , which we can learn solely from paired samples $(\bm{x},\bm{y})$ , and by Tweedie’s formula (Theorem 3.3), we can express these denoisers in terms of the score function of $p_{\bm{x}_{t}\mid\bm{y}}$ , which, by Bayes’ rule, satisfies

p_{\bm{x}_{t}\mid\bm{y}}(\bm{\xi}\mid\bm{\nu})=\frac{p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})p_{\bm{x}_{t}}(\bm{\xi})}{p_{\bm{y}}(\bm{\nu})}.

(6.3.12)

Recall that the density of $\bm{x}_{t}$ is given by $p_{t}=\varphi_{t}\ast p$ , where $\varphi_{t}$ denotes the standard Gaussian density with zero mean and covariance $t^{2}\bm{I}$ and $\ast$ denotes convolution. This is nothing but the unconditional score function obtained from the standard diffusion training that we developed in Section 3.2! The conditional score function then satisfies, for any realization $(\bm{\xi},\bm{\nu})$ of $(\bm{x}_{t},\bm{y})$ ,

\nabla_{\bm{\xi}}\log p_{\bm{x}_{t}\mid\bm{y}}(\bm{\xi}\mid\bm{\nu})=\underbrace{\nabla_{\bm{\xi}}\log p_{t}(\bm{\xi})}_{\text{score matching}}+\underbrace{\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})}_{\text{measurement matching}},

(6.3.13)

giving (by Tweedie’s formula) our proposed denoisers as

	$\displaystyle\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi},\bm{y}=\bm{\nu}]$	$\displaystyle=\bm{\xi}+t^{2}\nabla_{\bm{\xi}}\log p_{t}(\bm{\xi})+t^{2}\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})$
		$\displaystyle=\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]+t^{2}\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi}).$		(6.3.14)

The resulting operators are interpretable as a corrected version of the unconditional denoiser for the noisy observation, where the correction term (the so-called “measurement matching” term) enforces consistency with the observations $\bm{y}$ . The reader should take care to note to which argument the gradient operators are applying in the above score functions in order to fully grasp the meaning of this operator.

The key remaining issue in making this procedure computational is to prescribe how to compute the measurement matching correction, since in general we do not have a closed-form expression for the likelihood $p_{\bm{y}\mid\bm{x}_{t}}$ except for when $t=0$ . Before taking up this problem, we discuss an illustrative concrete example of the entire process, continuing from those we have developed in Section 3.2.

Example 6.2.

Consider the case where the data distribution is Gaussian with mean $\bm{\mu}\in\mathbb{R}^{D}$ and covariance $\bm{\Sigma}\in\mathbb{R}^{D\times D}$ , i.e., $\bm{x}\sim\mathcal{N}(\bm{\mu},\bm{\Sigma})$ . Assume that $\bm{\Sigma}\succeq\mathbf{0}$ is nonzero. Moreover, in the measurement model (6.3.9), suppose we obtain linear measurements of $\bm{x}$ with independent Gaussian noise, where $\bm{A}\in\mathbb{R}^{d\times D}$ and $\bm{y}=\bm{A}\bm{x}+\sigma\bm{w}$ with $\bm{w}\sim\mathcal{N}(\mathbf{0},\bm{I})$ independent of $\bm{x}$ . Then $\bm{x}=_{d}\bm{\Sigma}^{1/2}\bm{g}+\bm{\mu}$ , where $\bm{g}\sim\mathcal{N}(\mathbf{0},\bm{I})$ is independent of $\bm{w}$ and $\bm{\Sigma}^{1/2}$ is the unique positive square root of the covariance matrix $\bm{\Sigma}$ , and after some algebra, we can then write

\begin{bmatrix}\bm{x}\\ \bm{y}\end{bmatrix}=_{d}\begin{bmatrix}\bm{\Sigma}^{1/2}&\mathbf{0}\\ \bm{A}\bm{\Sigma}^{1/2}&\sigma\bm{I}\end{bmatrix}\begin{bmatrix}\bm{g}\\ \bm{w}\end{bmatrix}+\begin{bmatrix}\bm{\mu}\\ \bm{A}\bm{\mu}\end{bmatrix}.

By independence, we have that $(\bm{g},\bm{w})$ is jointly Gaussian, which means that $(\bm{x},\bm{y})$ is also jointly Gaussian, as the affine image of a jointly Gaussian vector. Its covariance matrix is given by

\begin{bmatrix}\bm{\Sigma}^{1/2}&\mathbf{0}\\ \bm{A}\bm{\Sigma}^{1/2}&\sigma\bm{I}\end{bmatrix}\begin{bmatrix}\bm{\Sigma}^{1/2}&\mathbf{0}\\ \bm{A}\bm{\Sigma}^{1/2}&\sigma\bm{I}\end{bmatrix}^{\top}=\begin{bmatrix}\bm{\Sigma}&\bm{\Sigma}\bm{A}^{\top}\\ \bm{A}\bm{\Sigma}&\bm{A}\bm{\Sigma}\bm{A}^{\top}+\sigma^{2}\bm{I}\end{bmatrix}.

Now, we apply the fact that conditioning a random vector with joint Gaussian distribution on a subset of coordinates is again a Gaussian distribution (Exercise 3.2). By this, we obtain that

p_{\bm{x}\mid\bm{y}}(\,\cdot\,\mid\bm{\nu})=\mathcal{N}\left(\underbrace{\bm{\mu}+\bm{\Sigma}\bm{A}^{\top}\left(\bm{A}\bm{\Sigma}\bm{A}^{\top}+\sigma^{2}\bm{I}\right)^{-1}(\bm{\nu}-\bm{A}\bm{\mu})}_{\bm{\mu}_{\bm{x}\mid\bm{y}}(\bm{\nu})},\underbrace{\bm{\Sigma}-\bm{\Sigma}\bm{A}^{\top}\left(\bm{A}\bm{\Sigma}\bm{A}^{\top}+\sigma^{2}\bm{I}\right)^{-1}\bm{A}\bm{\Sigma}}_{\bm{\Sigma}_{\bm{x}\mid\bm{y}}}\right).

(6.3.15)

By the equivalence we have derived above, we get by another application of Exercise 3.2

\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi},\bm{y}=\bm{\nu}]=\bm{\mu}_{\bm{x}\mid\bm{y}}(\bm{\nu})+\bm{\Sigma}_{\bm{x}\mid\bm{y}}\left(\bm{\Sigma}_{\bm{x}\mid\bm{y}}+t^{2}\bm{I}\right)^{-1}\left(\bm{\xi}-\bm{\mu}_{\bm{x}\mid\bm{y}}(\bm{\nu})\right).

(6.3.16)

The functional form of this denoiser is quite simple, but it carries an unwieldy dependence on the problem data $\bm{\mu}$ , $\bm{\Sigma}$ , $\bm{A}$ , and $\sigma^{2}$ . We can gain further insight into its behavior by comparing it with Equation 6.3.14. We have as usual

\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]=\bm{\mu}+\bm{\Sigma}\left(\bm{\Sigma}+t^{2}\bm{I}\right)^{-1}(\bm{\xi}-\bm{\mu}),

(6.3.17)

which is rather simple—suggesting that the measurement matching term is rather complicated. To confirm this, we can calculate the likelihood $p_{\bm{y}\mid\bm{x}_{t}}$ directly using the following expression for the joint distribution of $(\bm{x}_{t},\bm{y})$ :

\begin{bmatrix}\bm{x}\\ \bm{x}_{t}\\ \bm{y}\end{bmatrix}=_{d}\begin{bmatrix}\bm{\Sigma}^{1/2}&\mathbf{0}&\mathbf{0}\\ \bm{\Sigma}^{1/2}&t\bm{I}&\mathbf{0}\\ \bm{A}\bm{\Sigma}^{1/2}&\mathbf{0}&\sigma\bm{I}\end{bmatrix}\begin{bmatrix}\bm{g}\\ \bm{g}^{\prime}\\ \bm{w}\end{bmatrix}+\begin{bmatrix}\bm{\mu}\\ \bm{\mu}\\ \bm{A}\bm{\mu}\end{bmatrix},

(6.3.18)

where $\bm{g}^{\prime}\sim\mathcal{N}(\mathbf{0},\bm{I})$ independent of the other Gaussians. This is again a jointly Gaussian distribution; restricting to only the final two rows, we have the covariance

\begin{bmatrix}\bm{\Sigma}^{1/2}&t\bm{I}&\mathbf{0}\\ \bm{A}\bm{\Sigma}^{1/2}&\mathbf{0}&\sigma\bm{I}\end{bmatrix}\begin{bmatrix}\bm{\Sigma}^{1/2}&t\bm{I}&\mathbf{0}\\ \bm{A}\bm{\Sigma}^{1/2}&\mathbf{0}&\sigma\bm{I}\end{bmatrix}^{\top}=\begin{bmatrix}\bm{\Sigma}+t^{2}\bm{I}&\bm{\Sigma}\bm{A}^{\top}\\ \bm{A}\bm{\Sigma}&\bm{A}\bm{\Sigma}\bm{A}^{\top}+\sigma^{2}\bm{I}\end{bmatrix}.

Another application of Exercise 3.2 then gives us

p_{\bm{y}\mid\bm{x}_{t}}(\,\cdot\,\mid\bm{\xi})=\mathcal{N}\left(\underbrace{\bm{A}\bm{\mu}+\bm{A}\bm{\Sigma}\left(\bm{\Sigma}+t^{2}\bm{I}\right)^{-1}\left(\bm{\xi}-\bm{\mu}\right)}_{\bm{\mu}_{\bm{y}\mid\bm{x}_{t}}(\bm{\xi})},\underbrace{\bm{A}\bm{\Sigma}\bm{A}^{\top}+\sigma^{2}\bm{I}-\bm{A}\bm{\Sigma}\left(\bm{\Sigma}+t^{2}\bm{I}\right)^{-1}\bm{\Sigma}\bm{A}^{\top}}_{\bm{\Sigma}_{\bm{y}\mid\bm{x}_{t}}}\right).

(6.3.19)

Now notice that $\bm{\mu}_{\bm{y}\mid\bm{x}_{t}}(\bm{\xi})=\bm{A}\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]$ . So, by the chain rule,

	$\displaystyle t^{2}\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})$	$\displaystyle=t^{2}\nabla_{\bm{\xi}}\left[-\frac{1}{2}(\bm{\nu}-\bm{A}\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}])^{\top}\bm{\Sigma}_{\bm{y}\mid\bm{x}_{t}}^{-1}(\bm{\nu}-\bm{A}\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}])\right]$
		$\displaystyle=t^{2}(\bm{\Sigma}+t^{2}\bm{I})^{-1}\bm{\Sigma}\bm{A}^{\top}\bm{\Sigma}_{\bm{y}\mid\bm{x}_{t}}^{-1}\left(\bm{\nu}-\bm{A}\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]\right).$		(6.3.20)

This gives us a more interpretable decomposition of the conditional posterior denoiser (6.3.16): following Equation 6.3.14, it is the sum of the unconditional posterior denoiser (6.3.17) and the measurement matching term (6.3.20). We can further analyze the measurement matching term. Notice that

\bm{\Sigma}_{\bm{y}\mid\bm{x}_{t}}=\sigma^{2}\bm{I}+\bm{A}\bm{\Sigma}^{1/2}\left(\bm{I}-\bm{\Sigma}^{1/2}\left(\bm{\Sigma}+t^{2}\bm{I}\right)^{-1}\bm{\Sigma}^{1/2}\right)\bm{\Sigma}\bm{A}^{\top}.

(6.3.21)

If we let $\bm{\Sigma}=\bm{V}\bm{\Lambda}\bm{V}^{\top}$ denote an eigenvalue decomposition of $\bm{\Sigma}$ , where $(\bm{v}_{i})$ are the columns of $\bm{V}$ , we can further write

	$\displaystyle\bm{\Sigma}^{1/2}\left(\bm{I}-\bm{\Sigma}^{1/2}\left(\bm{\Sigma}+t^{2}\bm{I}\right)^{-1}\bm{\Sigma}^{1/2}\right)\bm{\Sigma}^{1/2}$	$\displaystyle=t^{2}\bm{V}\bm{\Lambda}^{1/2}\left(\bm{\Lambda}+t^{2}\bm{I}\right)^{-1}\bm{\Lambda}^{1/2}\bm{V}^{\top}$		(6.3.22)
		$\displaystyle=t^{2}\sum_{i=1}^{D}\frac{\lambda_{i}}{\lambda_{i}+t^{2}}\bm{v}_{i}\bm{v}_{i}^{\ast}.$		(6.3.23)

Then for any eigenvalue of $\bm{\Sigma}$ equal to zero, the corresponding summand is zero; and writing $\lambda_{\min}(\bm{\Sigma})$ for the smallest positive eigenvalue of $\bm{\Sigma}$ (it has at least one positive eigenvalue, by assumption), we have (in a sense that can be made quantitatively precise) that whenever $t\ll\sqrt{\lambda_{\min}(\bm{\Sigma})}$ , it holds

\frac{\lambda_{i}t^{2}}{\lambda_{i}+t^{2}}\approx 0.

(6.3.24)

So, when $t\ll\sqrt{\lambda_{\min}(\bm{\Sigma})}$ , we have the approximation

\bm{\Sigma}_{\bm{y}\mid\bm{x}_{t}}\approx\sigma^{2}\bm{I}.

(6.3.25)

The righthand side of this approximation is equal to $\bm{\Sigma}_{\bm{y}\mid\bm{x}}$ . So we have in turn

\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})\approx\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}}(\bm{\nu}\mid\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]).

(6.3.26)

Figure 6.9 : Numerical simulation of the conditional sampling setup ( 6.3.9 ), with Gaussian data, linear measurements, and Gaussian noise. We simulate D = 2 D=2 italic_D = 2 and d = 1 d=1 italic_d = 1 , with 𝚺 = 𝒆 1 𝒆 1 ⊤ + 1 4 𝒆 2 𝒆 2 ⊤ \bm{\Sigma}=\bm{e}_{1}\bm{e}_{1}^{\top}+\tfrac{1}{4}\bm{e}_{2}\bm{e}_{2}^{\top} bold_Σ = bold_italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT bold_italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT + divide start_ARG 1 end_ARG start_ARG 4 end_ARG bold_italic_e start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT bold_italic_e start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT , 𝝁 = 𝟎 \bm{\mu}=\mathbf{0} bold_italic_μ = bold_0 , and 𝑨 = 𝒆 1 ⊤ \bm{A}=\bm{e}_{1}^{\top} bold_italic_A = bold_italic_e start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT . The underlying signal 𝒙 \bm{x} bold_italic_x is marked with a black star, and the measurement 𝒚 \bm{y} bold_italic_y is marked with a black circle. Each individual plot corresponds to a different value of sampler time t ℓ t_{\ell} italic_t start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT , with different rows corresponding to different observation noise levels σ 2 \sigma^{2} italic_σ start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT . In each plot, the covariance matrix of 𝒙 \bm{x} bold_italic_x is plotted in gray, the posterior covariance matrix and posterior mean of p 𝒙 ∣ 𝒚 p_{\bm{x}\mid\bm{y}} italic_p start_POSTSUBSCRIPT bold_italic_x ∣ bold_italic_y end_POSTSUBSCRIPT are plotted in blue (with the posterior mean marked by a blue “x”), and contours for p 𝒙 t ℓ ∣ 𝒚 p_{\bm{x}_{t_{\ell}}\mid\bm{y}} italic_p start_POSTSUBSCRIPT bold_italic_x start_POSTSUBSCRIPT italic_t start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT end_POSTSUBSCRIPT ∣ bold_italic_y end_POSTSUBSCRIPT are drawn in green. The sampler hyperparameters are T = 1 T=1 italic_T = 1 , L = 100 L=100 italic_L = 100 , and we draw 100 100 100 independent samples to initialize the samplers. Samplers are implemented with the closed-form denoisers derived in Example 6.2 , with those using the approximation ( 6.3.26 ) marked with red triangles, and those using the exact conditional posterior denoiser marked with blue circles. Top: For large observation noise σ = 0.5 \sigma=0.5 italic_σ = 0.5 , both the exact conditional posterior denoiser and the approximate one do a good job of converging to the posterior p 𝒙 ∣ 𝒚 p_{\bm{x}\mid\bm{y}} italic_p start_POSTSUBSCRIPT bold_italic_x ∣ bold_italic_y end_POSTSUBSCRIPT . Sampling time (corresponding to time in the “forward process”, so larger times mean larger noise) decreases from left to right. The convergence dynamics for the exact and approximate measurement matching term are similar. Bottom: For smaller observation noise σ = 0.1 \sigma=0.1 italic_σ = 0.1 , the approximate measurement matching term leads to extreme bias in the sampler (red triangles): samples rapidly converge to an affine subspace of points that are consistent, modulo some shrinkage from the posterior mean denoiser, with the measured ground truth, and later sampling iterations are unable to recover the lost posterior variance along this dimension. Note that different times t ℓ t_{\ell} italic_t start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT are plotted in the bottom row, compared to the top row, to show the rapid collapse of the approximation to the posterior along the measurement dimension. — Figure 6.9: Numerical simulation of the conditional sampling setup (6.3.9), with Gaussian data, linear measurements, and Gaussian noise. We simulate $D=2$ and $d=1$ , with $\bm{\Sigma}=\bm{e}_{1}\bm{e}_{1}^{\top}+\tfrac{1}{4}\bm{e}_{2}\bm{e}_{2}^{\top}$ , $\bm{\mu}=\mathbf{0}$ , and $\bm{A}=\bm{e}_{1}^{\top}$ . The underlying signal $\bm{x}$ is marked with a black star, and the measurement $\bm{y}$ is marked with a black circle. Each individual plot corresponds to a different value of sampler time $t_{\ell}$ , with different rows corresponding to different observation noise levels $\sigma^{2}$ . In each plot, the covariance matrix of $\bm{x}$ is plotted in gray, the posterior covariance matrix and posterior mean of $p_{\bm{x}\mid\bm{y}}$ are plotted in blue (with the posterior mean marked by a blue “x”), and contours for $p_{\bm{x}_{t_{\ell}}\mid\bm{y}}$ are drawn in green. The sampler hyperparameters are $T=1$ , $L=100$ , and we draw $100$ independent samples to initialize the samplers. Samplers are implemented with the closed-form denoisers derived in Example 6.2, with those using the approximation (6.3.26) marked with red triangles, and those using the exact conditional posterior denoiser marked with blue circles. Top: For large observation noise $\sigma=0.5$ , both the exact conditional posterior denoiser and the approximate one do a good job of converging to the posterior $p_{\bm{x}\mid\bm{y}}$ . Sampling time (corresponding to time in the “forward process”, so larger times mean larger noise) decreases from left to right. The convergence dynamics for the exact and approximate measurement matching term are similar. Bottom: For smaller observation noise $\sigma=0.1$ , the approximate measurement matching term leads to extreme bias in the sampler (red triangles): samples rapidly converge to an affine subspace of points that are consistent, modulo some shrinkage from the posterior mean denoiser, with the measured ground truth, and later sampling iterations are unable to recover the lost posterior variance along this dimension. Note that different times $t_{\ell}$ are plotted in the bottom row, compared to the top row, to show the rapid collapse of the approximation to the posterior along the measurement dimension.

Equation 6.3.26 is, of course, a direct consequence of our calculations above. However, notice that if we directly interpret this approximation, it is ab initio tractable: the likelihood $p_{\bm{y}\mid\bm{x}}=\mathcal{N}(\bm{A}\bm{x},\sigma^{2}\bm{I})$ is a simple Gaussian distribution centered at the observation, and the approximation to the measurement matching term that we arrive at can be interpreted as simply evaluating the log-likelihood at the conditional expectation $\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]$ , then taking gradients with respect to $\bm{\xi}$ (and backpropagating through the conditional expectation, which is given here by Equation 6.3.17). Nevertheless, note that the approximation in Equation 6.3.26 requires $t\ll\sqrt{\lambda_{\min}(\bm{\Sigma})}$ , and that it is never accurate in general when this condition does not hold, even in this Gaussian setting.

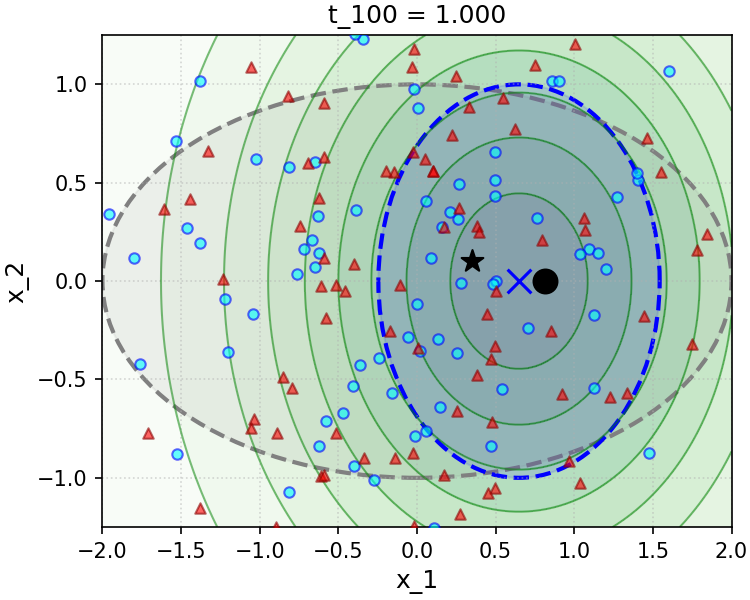
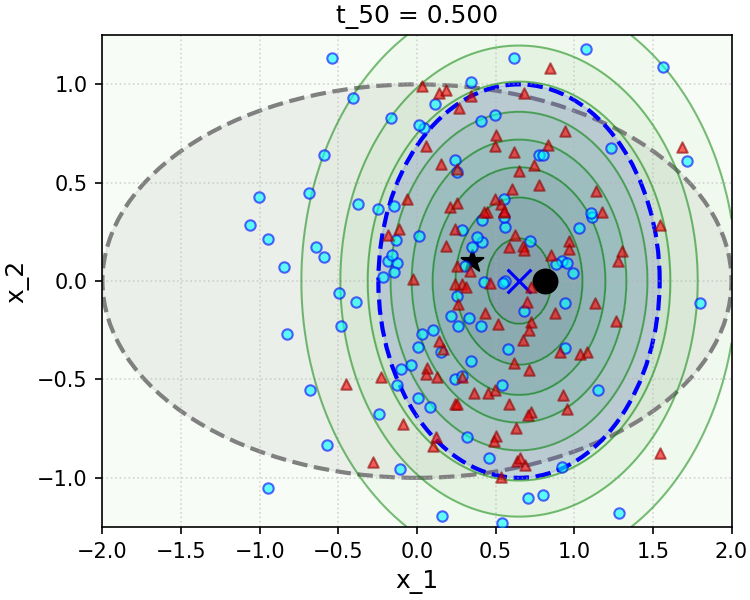
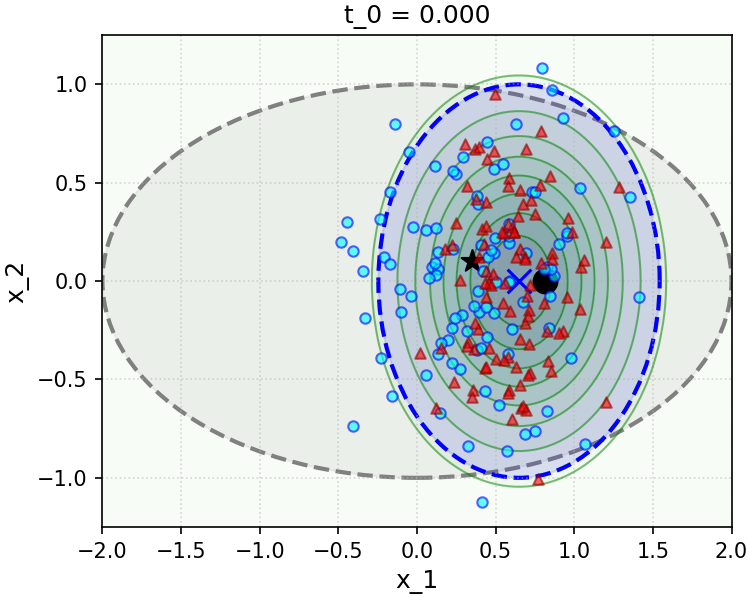
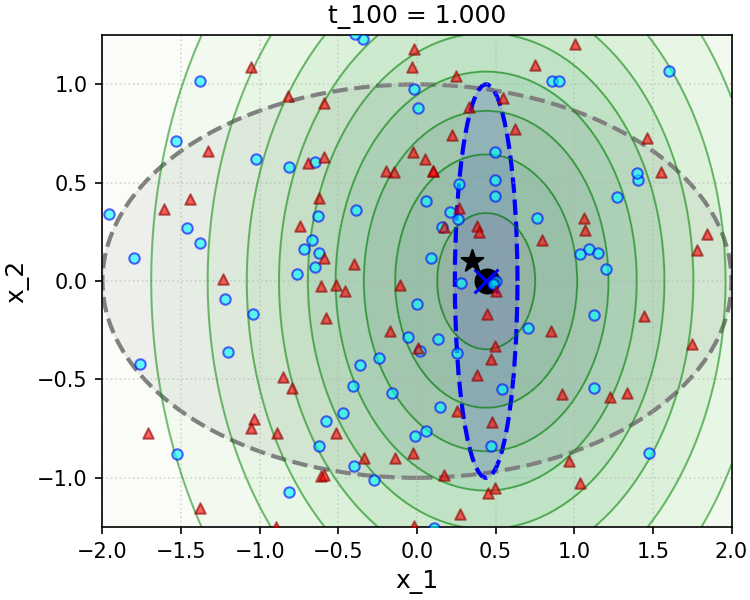
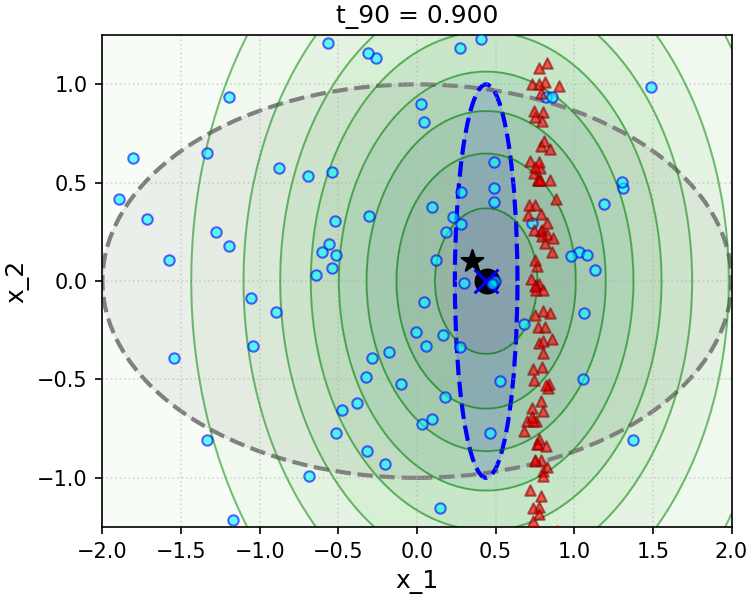
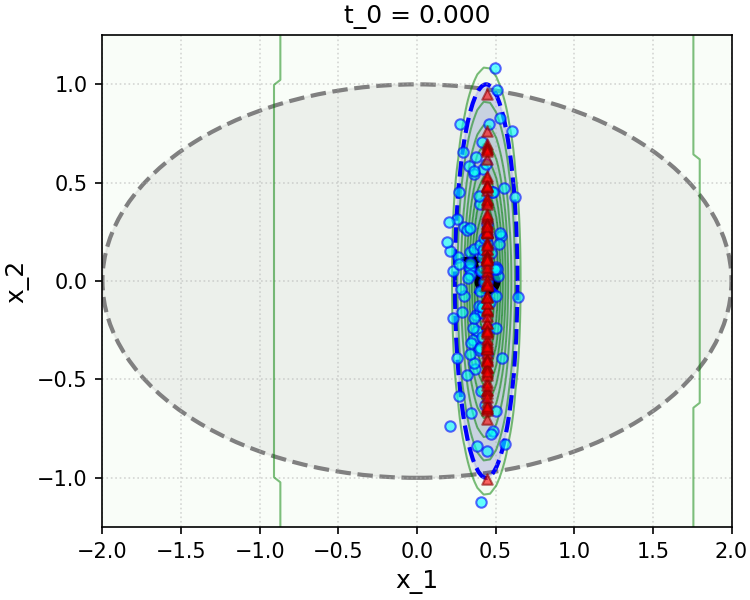
To gain insight into the effect of the convenient approximation (6.3.26), we implement and simulate a simple numerical experiment in the Gaussian setting in Figure 6.9. The sampler we implement is a direct implementation of the simple scheme (3.2.66) we have developed in Chapter 3 and recalled above, using the true conditional posterior denoiser, i.e. Equation 6.3.16 (top row of Figure 6.9), and the convenient approximation to this denoiser made with the decomposition (6.3.14), the posterior denoiser (6.3.17), and the measurement matching approximation (6.3.26) (bottom row of Figure 6.9). We see that even in the simple Gaussian setting, the approximation to the measurement matching term we have made is not without its drawbacks—specifically, at small noise levels $\sigma^{2}\ll 1$ , it leads to rapid collapse of the variance of the sampling distribution along directions that are parallel to the rows of the linear measurement operator $\bm{A}$ , which cannot be corrected by later iterations of sampling. We can intuit this from the approximation (6.3.26) and the definition of the denoising iteration (3.2.66), given Equation 6.3.14: for $\sigma^{2}\ll 1$ , early steps of sampling effectively take gradient descent steps with a very large step size on the likelihood, via Equation 6.3.26, which leads the sampling distribution to get “stuck” in a collapsed state.

$\blacksquare$

Example 6.2 suggests a convenient approximation for the measurement matching term (6.3.26), which can be made beyond the Gaussian setting of the example. To motivate this approximation in greater generality, notice that by conditional independence of $\bm{y}$ and $\bm{x}_{t}$ given $\bm{x}$ , we can write

p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})=\int p_{\bm{y}\mid\bm{x}}(\bm{\nu}\mid\bm{\xi}^{\prime})p_{\bm{x}\mid\bm{x}_{t}}(\bm{\xi}^{\prime}\mid\bm{\xi})\mathrm{d}\bm{\xi}^{\prime}.

(6.3.27)

Formally, when the posterior $p_{\bm{x}\mid\bm{x}_{t}}$ is a delta function centered at its mean $\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]$ , the approximation (6.3.26) is exact. More generally, when the posterior $p_{\bm{x}\mid\bm{x}_{t}}$ is highly concentrated around its mean, the approximation (6.3.26) is accurate. This holds, for example, for sufficiently small $t$ , which we saw explicitly in the Gaussian setting of Example 6.2. Although the numerical simulation in Figure 6.9 suggests that this approximation is not without its caveats in certain regimes, it has proved to be a reliable baseline in practice, after being proposed by Chung et al. as “Diffusion Posterior Sampling” (DPS) [CKM+23]. In addition, there are even principled and generalizable approaches to improve it by incorporating better estimates of the posterior variance (which turn out to be exact in the Gaussian setting of Example 6.2), which we discuss further in the end-of-chapter summary.

Thus, with the DPS approximation, we arrive at the following approximation for the conditional posterior denoisers $\mathbb{E}[\bm{x}\mid\bm{y},\bm{x}_{t}]$ , via Equation 6.3.14:

\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi},\bm{y}=\bm{\nu}]\approx\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]+t^{2}\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}}(\bm{\nu}\mid\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]).

(6.3.28)

And, for a neural network or other model $\bar{\bm{x}}_{\theta}(t,\bm{\xi})$ trained as in Section 3.2 to approximate the denoisers $\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]$ for each $t\in[0,T]$ , we arrive at the learned conditional posterior denoisers

\bar{\bm{x}}_{\theta}(t,\bm{\xi},\bm{\nu})=\bar{\bm{x}}_{\theta}(t,\bm{\xi})+t^{2}\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}}(\bm{\nu}\mid\bar{\bm{x}}_{\theta}(t,\bm{\xi})).

(6.3.29)

Note that the approximation (6.3.28) is valid for arbitrary forward models $h$ in the observation model (6.3.9), including nonlinear $h$ , and even to arbitrary noise models for which a clean expression for the likelihood $p_{\bm{y}\mid\bm{x}}$ is known. Indeed, in the case of Gaussian noise, we have

p_{\bm{y}\mid\bm{x}}(\bm{\nu}\mid\bm{\xi})\propto\exp\left(-\frac{1}{2\sigma^{2}}\left\|h(\bm{\xi})-\bm{\nu}\right\|_{2}^{2}\right).

(6.3.30)

Hence, evaluating the righthand side of (6.3.29) requires only

1.

A pretrained denoiser $\bar{\bm{x}}_{\theta}(t,\bm{\xi})$ for the data distribution $p$ (of $\bm{x})$ , learned as in Section 3.2 via Algorithm 3.2;
2.

Forward and backward pass access to the forward model $h$ for the measurements (6.3.9);
3.

A forward and backward pass through $\bar{\bm{x}}_{\theta}(t,\bm{\xi})$ , which can be evaluated efficiently using (say) backpropagation.

Algorithm 6.1 Conditional sampling under measurements (6.3.9), with an unconditional denoiser and DPS.

1:An ordered list of timesteps

0\leq t_{0}<\cdots<t_{L}\leq T

to use for sampling.

2:An unconditional denoiser

\bar{\bm{x}}_{\theta}\colon\{t_{\ell}\}_{\ell=1}^{L}\times\mathbb{R}^{D}\to\mathbb{R}^{D}

for

p_{\bm{x}}

3:Measurement realization

\bm{\nu}

\bm{y}

(Equation 6.3.9) to condition on.

4:Forward model

h:\mathbb{R}^{D}\to\mathbb{R}^{d}

and measurement noise variance

\sigma^{2}>0

5:Scale and noise level functions

\alpha,\sigma\colon\{t_{\ell}\}_{\ell=0}^{L}\to\mathbb{R}_{\geq 0}

6:A sample

\hat{\bm{x}}

, approximately from

p_{\bm{x}\mid\bm{y}}

7:function DDIMSamplerConditionalDPS(

\bar{\bm{x}}_{\theta},\bm{\nu},h,\sigma^{2},(t_{\ell})_{\ell=0}^{L}

)

8: Initialize

\hat{\bm{x}}_{t_{L}}\sim

approximate distribution of

\bm{x}_{t_{L}}

\triangleright

\implies\operatorname{\mathcal{N}}(\bm{0},\bm{I})

, VE

\implies\operatorname{\mathcal{N}}(\bm{0},t_{L}^{2}\bm{I})

9: for

\ell=L,L-1,\dots,1

10: Compute

\hat{\bm{x}}_{t_{\ell-1}}\doteq\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\hat{\bm{x}}_{t_{\ell}}+\left(\alpha_{t_{\ell-1}}-\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\alpha_{t_{\ell}}\right)\left(\bar{\bm{x}}_{\theta}(t_{\ell},\hat{\bm{x}}_{t_{\ell}})-\frac{\sigma_{t_{\ell}}^{2}}{2\alpha_{t_{\ell}}\sigma^{2}}\nabla_{\bm{\xi}}\left[\left\|h(\bar{\bm{x}}_{\theta}(t_{\ell},\bm{\xi}))-\bm{\nu}\right\|_{2}^{2}\right]\biggl{|}_{\bm{\xi}=\hat{\bm{x}}_{t_{\ell}}}\biggr{.}\right)

11: end for

12: return

\hat{\bm{x}}_{t_{0}}

13:end function

Combining this scheme with the basic implementation of unconditional sampling we developed in Section 3.2, we obtain a practical algorithm for conditional sampling of the posterior $p_{\bm{x}\mid\bm{y}}$ given measurements following (6.3.9). Algorithm 6.1 records this scheme for the case of Gaussian observation noise with known standard deviation $\sigma$ , with minor modifications to extend to a general noising process, as in Equation 3.2.69 and the surrounding discussion in Chapter 3 (our discussion above made the simplifying choices $\alpha_{t}=1$ , $\sigma_{t}=t$ , and $t_{\ell}=T\ell/L$ , as for Equation 3.2.66 in Section 3.2).

6.3.3 Body Pose Generation Conditioned on Head and Hands

This type of conditional estimation or generation problem arises rather naturally in many practical applications. A typical problem of this kind is how to estimate and generate body pose and hand gesture conditioned on a given head pose and egocentric images, as illustrated in Figure 6.10. This is often the problem we need to solve when one is wearing a head-mounted device such as the Vision Pro from Apple or the Project Aria from Meta. The pose of the whole body and the gesture of the hands need to be inferred so that we can use the information to control virtual objects that the person interacts with.

Figure 6.10 : A system that estimates human body height, pose, and hand parameters (middle), conditioned on egocentric SLAM poses and images (left). Outputs capture the wearer’s actions in the allocentric reference frame of the scene, which we visualize here with 3D reconstructions (right). — Figure 6.10: A system that estimates human body height, pose, and hand parameters (middle), conditioned on egocentric SLAM poses and images (left). Outputs capture the wearer’s actions in the allocentric reference frame of the scene, which we visualize here with 3D reconstructions (right).

Notice that in this case, one only has the head pose provided by the device and a very limited field of view for part of one’s hands and upper limbs. The pose of the rest of the body needs to be “inferred” or “completed” based on such partial information. The only way one can estimate the body pose over time is by learning the joint distribution of the head and body pose sequences in advance and then sampling this prior distribution conditioned on the real-time partial inputs. Figure 6.11 outlines a system called EgoAllo [YYZ+24] to solve this problem based on a learned conditional diffusion-denoising model.

Figure 6.11 : Overview of technical components of EgoAllo [ YYZ+24 ] . A diffusion model is pretrained that can generate body pose sequence based on local body parameters (middle). An invariant parameterization g ( ⋅ ) g(\cdot) italic_g ( ⋅ ) of SLAM poses (left) is used to condition the diffusion model. These can be placed into the global coordinate frame via global alignment to input poses. When available, egocentric video is used for hand detection (left) via HaMeR [ PSR+23 ] , which can be incorporated into samples via guidance by the generated gesture. — Figure 6.11: Overview of technical components of EgoAllo [YYZ+24]. A diffusion model is pretrained that can generate body pose sequence based on local body parameters (middle). An invariant parameterization $g(\cdot)$ of SLAM poses (left) is used to condition the diffusion model. These can be placed into the global coordinate frame via global alignment to input poses. When available, egocentric video is used for hand detection (left) via HaMeR [PSR+23], which can be incorporated into samples via guidance by the generated gesture.

Figure 6.12 compares some ground truth motion sequences with sampled results generated by the EgoAllo. Although the figure shows one result for each input head pose sequence, different runs can generate different body pose sequences that are consistent with the given head pose, all drawing from the distribution of natural full-body motion sequences.

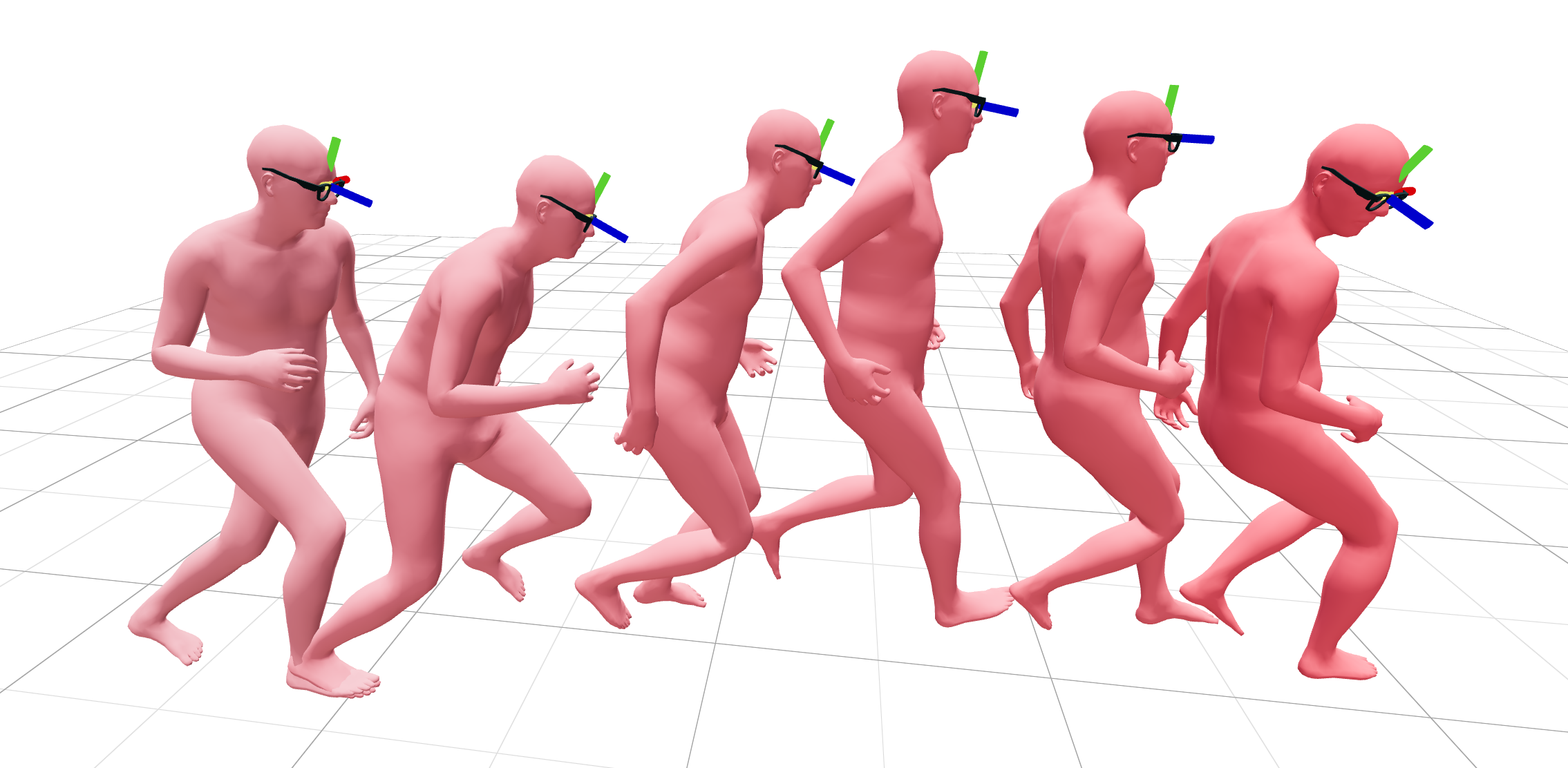
Strictly speaking, the solution proposed in EgoAllo [YYZ+24] does not enforce measurement matching using the techniques introduced above. Instead it heuristically enforces the condition by utilizing the cross-attention mechanism in a transformer architecture. As we will describe with more precision in the paired data setting in Section 6.4.2, there is reason to believe that the cross-attention mechanism is in a way approximately realizing the conditional sampling of the denoising a posteriori. We believe the more principled techniques introduced here, if properly implemented, can lead to better methods that further improve the body pose and hand gesture estimation.

6.4 Conditional Inference with Paired Data and Measurements

In many practical applications, we do not know either the distribution of the data $\bm{x}$ of interest or the explicit relationship between the data and certain observed attributes $\bm{y}$ of the data. We only have a (large) set of paired samples $(\bm{X},\bm{Y})=\{(\bm{x}_{1},\bm{y}_{1}),\ldots,(\bm{x}_{N},\bm{y}_{N})\}$ from which we need to infer the data distribution and a mapping that models their relationship:

h:\bm{x}\mapsto\bm{y}.

(6.4.1)

The problem of image classification can be viewed as one such example. In a sense, the classification problem is to learn an (extremely lossy) compressive encoder for natural images. Say, given a random sample of an image $\bm{x}$ , we would like to predict its class label $\bm{y}$ that best correlates the content in $\bm{x}$ . We know the distribution of natural images of objects is low-dimensional compared to the dimension of the pixel space. From the previous chapters, we have learned that given sufficient samples, in principle, we can learn a structured low-dimensional representation $\bm{z}$ for $\bm{x}$ through a learned compressive encoding:

f:\bm{x}\mapsto\bm{z}.

(6.4.2)

The representation $\bm{z}$ can also be viewed as a learned (lossy but structured) code for $\bm{x}$ . It is rather reasonable to assume that if the class assignment $\bm{y}$ truly depends on the low-dimensional structures of $\bm{x}$ and the learned code $\bm{z}$ truly reflects such structures, $\bm{y}$ and $\bm{z}$ can be made highly correlated and hence their joint distribution $p(\bm{z},\bm{y})$ should be extremely low-dimensional. Therefore, we may combine the two desired codes $\bm{y}$ and $\bm{z}$ together and try to learn a combined encoder:

f:\bm{x}\mapsto(\bm{z},\bm{y})

(6.4.3)

where the joint distribution of $(\bm{z},\bm{y})$ is highly low-dimensional.

From our study in previous chapters, the mapping $f$ is usually learned as a sequence of compression or denoising operators in the same space. Hence to leverage such a family of operations, we may introduce an auxiliary vector $\bm{w}$ that can be viewed as an initial random guess of the class label $\bm{y}$ . In this way, we can learn a compression or denoising mapping:

f:(\bm{x},\bm{w})\mapsto(\bm{z},\bm{y})

(6.4.4)

within a common space. In fact, the common practice of introducing an auxiliary “class token” in the training of a transformer for classification tasks, such as in ViT, can be viewed as learning such a representation by compressing (the coding rate of) given (noisy) samples of $(\bm{x},\bm{w})$ . If the distribution of the data $\bm{x}$ is already a mixture of (low-dimensional) Gaussians, the work [WTL+08] has shown that classification can be done effectively by directly minimizing the (lossy) coding length associated with the given samples.

6.4.1 Class Conditioned Image Generation

While a learned classifier allows us to classify a given image $\bm{x}$ to its corresponding class, we often would like to generate an image of a given class, by sampling the learned distribution of natural images. To some extent, this can be viewed as the “inverse” problem to image classification. Let $p_{\bm{x}}$ denote the distribution of natural images, say modeled by a diffusion-denoising process. Given a class label random variable $y\in[K]$ with realization $\nu$ , say an “Apple”, we would like to sample the conditional distribution $p_{\bm{x}\mid y}(\,\cdot\,\mid\nu)$ to generate an image of an apple:

\hat{\bm{x}}\sim p_{\bm{x}\mid\bm{y}}(\,\cdot\,\mid\bm{\nu}).

(6.4.5)

We call this class-conditioned image generation.

In Section 6.3.2, we have seen how to use the denoising-diffusion paradigm for conditional sampling from the posterior $p_{\bm{x}\mid\bm{y}}$ given model-based measurements $\bm{y}=h(\bm{x})+\bm{w}$ (Equation 6.3.9), culminating in the DPS algorithm (Algorithm 6.1). This is a powerful framework, but it does not apply to the class (or text) conditioned image generation problem here, where an explicit generative model $h$ for the observations/attributes $y$ is not available due to the intractability of analytical modeling. In this section, we will present techniques for extending conditional sampling to this setting.

Thus, we now assume only that we have access to samples from the joint distribution of $(\bm{x},y)$ :

(\bm{x},y)\sim p_{\bm{x},y}.

(6.4.6)

As in the previous section, we define $\bm{x}_{t}=\alpha_{t}\bm{x}+\sigma_{t}\bm{g}$ with $\bm{g}\sim\mathcal{N}(\mathbf{0},\bm{I})$ independent of $(\bm{x},\bm{y})$ , as in Equation 3.2.69 in Chapter 3, and we will repeatedly use the notation $\bm{\xi}$ to denote realizations of $\bm{x}$ and $\bm{x}_{t}$ .

To proceed, we note that our development of conditional sampling under measurements $\bm{y}=h(\bm{x})+\bm{w}$ only explicitly used the forward model $h$ in making the DPS approximation (6.3.26). In particular, the conditional posterior denoiser decomposition (6.3.14) still holds in the paired data setting, by virtue of Bayes’ rule and conditional independence of $\bm{y}$ and $\bm{x}_{t}$ given $\bm{x}$ (recall Figure 6.8). Thus we can still write in the paired data setting

\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi},y=\nu]=\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]+\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{\xi}}\log p_{y\mid\bm{x}_{t}}(\nu\mid\bm{\xi}).

(6.4.7)

A natural ideal is then to directly implement the likelihood correction term in (6.4.7) using a deep network $f_{\theta_{\mathrm{c}}}$ with parameters $\theta_{\mathrm{c}}$ , as in Equation 6.4.4:

f_{\theta_{\mathrm{c}}}:(t,\bm{x}_{t})\mapsto\operatorname{\mathrm{softmax}}(\bm{W}_{\mathrm{head}}\bm{z}(t,\bm{x}_{t})).

(6.4.8)

This expression combines the final representations $\bm{z}(t,\bm{x}_{t})$ (which also depend on $\theta_{\mathrm{c}}$ ) of the noisy inputs $\bm{x}_{t}$ with a classification head $\bm{W}_{\mathrm{head}}\in\mathbb{R}^{K\times d}$ , which maps the representations to a probability distribution over the $K$ possible classes. As is common in practice, it also takes the time $t$ in the noising process as input. Thus, with appropriate training, it provides an approximation to the log-likelihood $\log p_{y\mid\bm{x}_{t}}$ , and differentiating $\log f_{\theta_{\mathrm{c}}}$ with respect to its input $\bm{x}_{t}$ allows an approximation to the second term in Equation 6.4.7:

\bar{\bm{x}}_{\theta}^{\mathrm{naive}}(t,\bm{x}_{t},y)=\bar{\bm{x}}_{\theta_{\mathrm{d}}}(t,\bm{x}_{t})+\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{x}_{t}}\left\langle\log f_{\theta_{\mathrm{c}}}(t,\bm{x}_{t}),\bm{e}_{y}\right\rangle

(6.4.9)

where, as usual, we approximate the first term in Equation 6.4.7 via a learned unconditional denoiser for $\bm{x}_{t}$ with parameters $\theta_{\mathrm{d}}$ , and where we write $\bm{e}_{k}$ for $k\in[K]$ to denote the $k$ -th canonical basis vector for $\mathbb{R}^{K}$ (i.e., the vector with a one in the $k$ -th position, and zeros elsewhere). The reader should note that the conditional denoiser $\bar{\bm{x}}_{\theta}$ requires two separate training runs, with separate losses: one for the classifier parameters $\theta_{\mathrm{c}}$ , on a classification loss,⁸⁸8In Chapter 7, we review the process of training such a classifier in full detail. and one for the denoiser parameters $\theta_{\mathrm{d}}$ , on a denoising loss. Such an approach to conditional sampling was already recognized and exploited to perform conditional sampling in pioneering early works on diffusion models, notably those by [SWM+15] and by [SSK+21].

However, this straightforward methodology has two key drawbacks (which is why we label it as “naive”). The first is that, empirically, such a trained deep network classifier frequently does not provide a strong enough guidance signal (in Equation 6.4.7) to ensure that generated samples reflect the conditioning information $y$ . This was first emphasized by [DN21], who noted that in the setting of class-conditional ImageNet generation, the learned deep network classifier’s probability outputs for the class $y$ being conditioned on were frequently around $0.5$ —large enough to be the dominant class, but not large enough to provide a strong guidance signal—and that upon inspection, generations were not consistent with the conditioning class $y$ . [DN21] proposed to address this heuristically by incorporating an “inverse temperature” hyperparameter $\gamma>0$ into the definition of the naive conditional denoiser (6.4.9), referring to the resulting conditional denoiser as having incorporated “classifier guidance” (CG):

\bar{\bm{x}}_{\theta}^{\mathrm{CG}}(t,\bm{x}_{t},y)=\bar{\bm{x}}_{\theta_{\mathrm{d}}}(t,\bm{x}_{t})+\gamma\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{x}_{t}}\left\langle\log f_{\theta_{\mathrm{c}}}(t,\bm{x}_{t}),\bm{e}_{y}\right\rangle

(6.4.10)

with the case $\gamma=1$ coinciding with (6.4.9). [DN21] found that a setting $\gamma>1$ performed best empirically. One possible interpretation for this is as follows: note that, in the context of the true likelihood term Equation 6.4.7, scaling by $\gamma$ gives equivalently

\displaystyle\gamma\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{\xi}}\log p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})

\displaystyle=\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{\xi}}\log\left(p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})^{\gamma}\right),

(6.4.11)

which suggests the natural interpretation of the parameter $\gamma$ performing (inverse) temperature scaling on the likelihood $p_{\bm{y}\mid\bm{x}_{t}}$ , which is precise if we consider the renormalized distribution ${p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}\mid\bm{\xi})^{\gamma}}/{\int p_{\bm{y}\mid\bm{x}_{t}}(\bm{\nu}^{\prime}\mid\bm{\xi})^{\gamma}\mathrm{d}\bm{\nu}^{\prime}}$ . However, note that this is not a rigorous interpretation in the context of Equation 6.4.7, because the gradients are taken with respect to $\bm{\xi}$ , and the normalization constant in the temperature-scaled distribution is in general a function of $\bm{\xi}$ . Instead, the parameter $\gamma$ should simply be understood as amplifying large values of the deep network classifier’s output probabilities $f_{\theta_{\mathrm{c}}}(t,\bm{x}_{t})$ relative to smaller ones, which effectively amplifies the guidance signal provided in cases where the deep network $f$ assigns it the largest probability among the $K$ classes.

Nevertheless, classifier guidance does not address the second key drawback of the naive methodology: it is both cumbersome and wasteful to have to train an auxiliary classifier $f_{\theta_{\mathrm{c}}}$ in addition to the unconditional denoiser $\bar{\bm{x}}_{\theta_{\mathrm{d}}}$ , given that it is not possible to directly adapt a pretrained classifier due to the need for it to work well on noisy inputs $\bm{x}_{t}$ and incorporate other empirically-motivated architecture modifications. In particular, [DN21] found that it was necessary to explicitly design the architecture of the deep network implementing the classifier to match that of the denoiser. Moreover, from a purely practical perspective—trying to obtain the best possible performance from the resulting sampler—the best-performing configuration of classifier guidance-based sampling departs even further from the idealized and conceptually sound framework we have presented above. To obtain the best performance, [DN21] found it necessary to provide the class label $y$ as an additional input to the denoiser $\bar{\bm{x}}_{\theta_{\mathrm{d}}}$ . As a result, the idealized classifier-guided denoiser (6.4.10), derived by [DN21] as we have done above from the conditional posterior denoiser decomposition (6.4.7), is not exactly reflective of the best-performing denoiser in practice—such a denoiser actually combines a conditional denoiser for $\bm{x}_{t}$ given $y$ with an additional guidance signal from an auxiliary classifier!

This state of affairs, empirically motivated as it is, led [HS22] in subsequent work to propose a more empirically pragmatic methodology, known as classifier-free guidance (CFG). Instead of representing the conditional denoiser (6.4.7) as a weighted sum of an unconditional denoiser for $\bm{x}_{t}$ with a log-likelihood correction term (with possibly modified weights, as in classifier guidance), they accept the apparent necessity of training a conditional denoiser for $\bm{x}_{t}$ given $y$ , as demonstrated by the experimental results of [DN21], and replace the log-likelihood gradient term with a correctly-weighted sum of this conditional denoiser with an unconditional denoiser for $\bm{x}$ given $\bm{x}_{t}$ .⁹⁹9That said, [HS22] actually proposed to use a different weighting than what we present here, based on the fact that [DN21] heuristically replaced the unconditional denoiser in (6.4.7) with a conditional denoiser. In fact, the weighting we derive and present here reflects modern practice, and in particular is used in state-of-the-art diffusion models such as Stable Diffusion 3.5 [EKB+24]. To see how this structure arises, we begin with an ‘idealized’ version of the classifier guidance denoiser $\bar{\bm{x}}_{\theta}^{\mathrm{CG}}$ defined in (6.4.10), for which the denoiser $\bar{\bm{x}}_{\theta_{\mathrm{d}}}$ and the classifier $f_{\theta_{\mathrm{c}}}$ perfectly approximate their targets, via (6.4.7):

\bar{\bm{x}}_{\theta}^{\mathrm{CG,\,ideal}}(t,\bm{\xi},\nu)=\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]+\gamma\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{\xi}}\log p_{y\mid\bm{x}_{t}}(\nu\mid\bm{\xi}).

(6.4.12)

We then use Bayes’ rule, in the form

\log p_{y\mid\bm{x}_{t}}=\log p_{\bm{x}_{t}\mid y}+\log p_{y}-\log p_{\bm{x}_{t}},

(6.4.13)

together with Tweedie’s formula (Theorem 3.3, modified as in Equation 3.2.70) to convert between score functions and denoisers, to obtain

	$\displaystyle\bar{\bm{x}}_{\theta}^{\mathrm{CG,\,ideal}}(t,\bm{\xi},\nu)$	$\displaystyle=\frac{1}{\alpha_{t}}\bm{\xi}+(1-\gamma)\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{\xi}}\log p_{\bm{x}_{t}}(\bm{\xi})+\gamma\frac{\sigma_{t}^{2}}{\alpha_{t}}\nabla_{\bm{\xi}}\log p_{\bm{x}_{t}\mid y}(\bm{\xi}\mid\nu)$
		$\displaystyle=(1-\gamma)\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]+\gamma\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi},y=\nu],$		(6.4.14)

where in the last line, we apply Equation 6.3.11. Now, Equation 6.4.14 suggests a natural approximation strategy: we combine a learned unconditional denoiser for $\bm{x}$ given $\bm{x}_{t}$ , as previously, with a learned conditional denoiser for $\bm{x}$ given $\bm{x}_{t}$ and $y$ .

However, following [HS22] and the common practice of training deep network denoisers, it is standard to use the same deep network to represent both the conditional and unconditional denoisers by introducing an additional label, which we will denote by $\varnothing$ , to denote the “unconditional” case. This leads to the form of the CFG denoiser:

\bar{\bm{x}}_{\theta}^{\mathrm{CFG}}(t,\bm{x}_{t},y)=(1-\gamma)\bar{\bm{x}}_{\theta}(t,\bm{x}_{t},\varnothing)+\gamma\bar{\bm{x}}_{\theta}(t,\bm{x}_{t},y).

(6.4.15)

To train a denoiser $\bar{\bm{x}}_{\theta}(t,\bm{x}_{t},y^{+})$ for use with classifier-free guidance sampling, where $y^{+}\in\{1,\dots,K,\varnothing\}$ , we proceed almost identically to the unconditional training procedure in Algorithm 3.2, but with two modifications:

1.

When we sample from the dataset, we sample a pair $(\bm{x},y)$ rather than just a sample $\bm{x}$ .

Every time we sample a pair from the dataset, we sample the augmented label $y^{+}$ via

y^{+}=\begin{cases}\varnothing&\text{with probability }p_{\mathrm{uncond}};\\ y&\text{else}.\end{cases}

(6.4.16)

Here, $p_{\mathrm{uncond}}\in[0,1]$ is a new hyperparameter. This can be viewed as a form of dropout [SHK+14].

In this way, we train a conditional denoiser suitable for use in classifier-free guidance sampling. We summarize the overall sampling process for class-conditioned sampling with classifier-free guidance in Algorithm 6.2.

Algorithm 6.2 Conditional sampling with classification data, using class-conditioned denoiser.

1:An ordered list of timesteps

0\leq t_{0}<\cdots<t_{L}\leq T

to use for sampling.

2:Class label

\nu\in\{1,\dots,K\}

to condition on.

3:A denoiser

\bar{\bm{x}}_{\theta}\colon\{t_{\ell}\}_{\ell=1}^{L}\times\mathbb{R}^{D}\times\{1,\dots,K,\varnothing\}\to\mathbb{R}^{D}

for

p_{\bm{x}\mid y}

and

p_{\bm{x}}

(input

\varnothing

for

p_{\bm{x}}

4:Scale and noise level functions

\alpha,\sigma\colon\{t_{\ell}\}_{\ell=0}^{L}\to\mathbb{R}_{\geq 0}

5:Guidance strength

\gamma\geq 0

(

\gamma>1

preferred for performance).

6:A sample

\hat{\bm{x}}

, approximately from

p_{\bm{x}\mid y}(\,\cdot\,\mid\nu)

7:function DDIMSamplerConditionalCFG(

\bar{\bm{x}}_{\theta},\nu,\gamma,(t_{\ell})_{\ell=0}^{L}

)

8: Initialize

\hat{\bm{x}}_{t_{L}}\sim

approximate distribution of

\bm{x}_{t_{L}}

\triangleright

\implies\operatorname{\mathcal{N}}(\bm{0},\bm{I})

, VE

\implies\operatorname{\mathcal{N}}(\bm{0},t_{L}^{2}\bm{I})

9: for

\ell=L,L-1,\dots,1

10: Compute

\hat{\bm{x}}_{t_{\ell-1}}\doteq\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\hat{\bm{x}}_{t_{\ell}}+\left(\alpha_{t_{\ell-1}}-\frac{\sigma_{t_{\ell-1}}}{\sigma_{t_{\ell}}}\alpha_{t_{\ell}}\right)\bigl{(}(1-\gamma)\bar{\bm{x}}_{\theta}(t_{\ell},\hat{\bm{x}}_{t_{\ell}},\varnothing)+\gamma\bar{\bm{x}}_{\theta}(t_{\ell},\hat{\bm{x}}_{t_{\ell}},\nu)\bigr{)}

11: end for

12: return

\hat{\bm{x}}_{t_{0}}

13:end function

[HS22] reports strong empirical performance for class-conditional image generation with classifier-free guidance, and it has become a mainstay of the largest-scale practical diffusion models, such as Stable Diffusion [RBL+22] and its derivatives. At the same time, its derivation is rather opaque and empirically motivated, giving little insight into the mechanisms behind its strong performance. A number of theoretical works have studied this, providing explanations for some parts of the overall CFG methodology [BN24a, LWQ25, WCL+24]—itself encompassing denoiser parameterization and training, as well as configuration of the guidance strength and performance at sampling time. Below, we will give an interpretation in the simplifying setting of a Gaussian mixture model data distribution and denoiser, which will demonstrate an insight into the parameterization of the denoiser in the presence of such low-dimensional structures.

Example 6.3.

Let us recall the low-rank mixture of Gaussians data generating process we studied in Example 3.2 (and specifically, the form in Equation 3.2.42). Given $K\in\mathbb{N}$ classes, we assume that

\bm{x}\sim\frac{1}{K}\sum_{k=1}^{K}\operatorname{\mathcal{N}}(\bm{0},\bm{U}_{k}\bm{U}_{k}^{\top}),

(6.4.17)

where each $\bm{U}_{k}\in\mathsf{O}(D,P)\subseteq\mathbb{R}^{D\times P}$ is a matrix with orthogonal columns, and $P\ll D$ . Moreover, we assume that the class label $y\in[K]$ is a deterministic function of $\bm{x}$ mapping an example to its corresponding mixture component. Applying the analysis in Example 3.2 (and the subsequent analysis of the low-rank case, culminating in Equation 3.2.56), we obtain for the class-conditional optimal denoisers

\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi},y=\nu]=\frac{1}{1+t^{2}}\bm{U}_{\nu}\bm{U}_{\nu}^{\top}\bm{\xi}

(6.4.18)

for each $\nu\in[K]$ , and for the optimal unconditional denoiser, we obtain

\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]=\frac{1}{1+t^{2}}\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{k}^{\top}\bm{\xi}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{\xi}\|_{2}^{2}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{\xi}.

(6.4.19)

As a result, we can express the CFG denoiser with guidance strength $\gamma>1$ as

\bar{\bm{x}}^{\mathrm{CFG,\,ideal}}(t,\bm{x}_{t},y)=\frac{1}{1+t^{2}}\left((1-\gamma)\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{k}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}+\gamma\bm{U}_{y}\bm{U}_{y}^{\top}\right)\bm{x}_{t}.

(6.4.20)

This denoiser has a simple, interpretable form. The first term, corresponding to the unconditional denoiser, performs denoising of the signal $\bm{x}_{t}$ against an average of the denoisers associated with each subspace, weighted by how correlated $\bm{x}_{t}$ is with each subspace. The second term, corresponding to the conditional denoiser, simply performs denoising with the conditioning class’s denoiser. The CFG scheme further averages these two denoisers: the effect can be gleaned from the refactoring

\begin{split}\bar{\bm{x}}^{\mathrm{CFG,\,ideal}}(t,\bm{x}_{t},y)=\frac{1}{1+t^{2}}&\Biggl{(}\left[\gamma+(1-\gamma)\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{y}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}\right]\bm{U}_{y}\bm{U}_{y}^{\top}\\ &\quad+(1-\gamma)\sum_{k\neq y}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{k}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}\Biggr{)}\bm{x}_{t}.\end{split}

(6.4.21)

We have

\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{k}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}=1,

(6.4.22)

and each summand is nonnegative, hence also bounded above by $1$ . So we can conclude two regimes for the terms in Equation 6.4.21:

Well-correlated regime: If $\bm{x}_{t}$ correlates well with $\bm{U}_{y}$ , then the normalized weight corresponding to the $k=y$ summand in the unconditional denoiser is near to $1$ . Then

\gamma+(1-\gamma)\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{y}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}\approx 1,

(6.4.23)

all other weights are necessarily near to zero, and the CFG denoiser is approximately equal to the denoiser associated to the conditioning class $y$ .

Poorly-correlated regime: In contrast, if $\bm{x}_{t}$ does not correlate well with $\bm{U}_{y}$ (say because $t$ is large), then the normalized weight corresponding to the $k=y$ summand in the unconditional denoiser is near to $0$ . As a result,

\gamma+(1-\gamma)\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{y}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{i}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}\approx\gamma,

(6.4.24)

and thus the guidance strength $\gamma\gg 1$ places a large positive weight on the denoiser associated to $y$ . Meanwhile, in the second term of Equation 6.4.21, any classes $k\neq y$ that are well-correlated with $\bm{x}_{t}$ receive a large negative weight from the $1-\gamma$ coefficient. This simultaneously has the effect of making the denoised signal vastly more correlated with the conditioning class $y$ , and making it negatively correlated with the previous iterate (i.e., the iterate before denoising). In other words, CFG steers the iterative denoising process towards the conditioning class and away from the previous iterate, a different dynamics from purely conditional sampling (i.e., the case $\gamma=1$ ).

We now perform a further analysis of the form of this guided denoiser in order to make some inferences about the role of CFG. Many of these insights will be relevant to general data distributions with low-dimensional geometric structure, as well. First, notice that the CFG denoiser (6.4.20) takes a simple form in the setting where $\bm{x}_{t}$ correlates significantly more strongly with a single subspace $\bm{U}_{y}$ than any other $\bm{U}_{y^{\prime}}$ . Indeed, because the ratio of weights in the class-conditional denoiser is given by

\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{y}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\|\bm{U}_{y^{\prime}}^{\top}\bm{x}_{t}\|_{2}^{2}\right)}=\exp\left(\frac{1}{2t^{2}(1+t^{2})}\left(\|\bm{U}_{y}^{\top}\bm{x}_{t}\|_{2}^{2}-\|\bm{U}_{y^{\prime}}^{\top}\bm{x}_{t}\|_{2}^{2}\right)\right),

(6.4.25)

a large separation between the correlation of $\bm{x}_{t}$ with $\bm{U}_{y}$ and other subspaces $\bm{U}_{y^{\prime}}$ implies that the sum over $k$ concentrates on the $k=y$ summand, giving that the CFG denoiser remains equal to the class-conditioned denoiser. Moreover, when $t\approx 0$ , the magnitude of any such gap is amplified in the exponential, making this concentration on the $k=y$ summand even stronger. In particular, for small times $t$ (i.e., near to the support of the data distribution), CFG denoising is no different from standard class-conditional denoising—implying that it will converge stably once it has reached such a configuration. Thus, the empirical benefits of CFG should be due to its behavior in cases where $\bm{x}_{t}$ is not unambiguously from a single class.

Next, we consider the problem of parameterizing a learnable denoiser $\bm{x}_{\theta}^{\mathrm{CFG}}$ to represent the optimal denoiser (6.4.20). Here, it may initially seem that the setting of classification of a mixture distribution is too much of a special case relative to learning practical data distributions, as the ideal denoiser (6.4.20) has in this setting the simple form of a hard assignment of the noisy signal $\bm{x}_{t}$ to the (denoiser associated to) the subspace $\bm{U}_{y}$ corresponding to the true class label $y$ of $\bm{x}$ , averaged with the soft assignment denoiser associated to all subspaces $\bm{U}_{k}$ , with weights given by the correlations of $\bm{x}_{t}$ with these different subspaces. However, we can extract a more general form for the class-conditional denoiser in this example which is relevant for practical parameterization using the geometric structure of the mixture of Gaussians distribution, which actually parallels the kinds of geometric structure common in real-world data. More precisely, we add an additional assumption associated to the subspaces $\bm{U}_{k}$ being ‘distinguishable’ from one another, which is natural in practice: specifically, we assume that for any pair of indices $k,k^{\prime}\in[K]$ with $k\neq k^{\prime}$ , we can find a set of $K$ directions $\bm{v}_{k}\in\mathbb{R}^{D}$ such that

\bm{U}_{k}\bm{U}_{k}^{\top}\bm{v}_{k}=\bm{v}_{k},\quad\bm{U}_{k^{\prime}}\bm{U}_{k^{\prime}}^{\top}\bm{v}_{k}=\mathbf{0},\enspace k^{\prime}\neq k.

(6.4.26)

This is a slightly stronger assumption than simple distinguishability, but it should be noted that it is not overly restrictive: for example, it still allows the subspaces $\bm{U}_{k}$ to have significant correlations with one another.¹⁰¹⁰10 More generally, this assumption is naturally formulated as an incoherence condition between the subspaces $\bm{U}_{[K]}$ , a familiar notion from the theory of compressive sensing. These vectors $\bm{v}_{k}$ can then be thought of as embeddings of the class label $y\in[K]$ , and we can use them to define a more general operator that can represent both the unconditional and class-conditional denoisers. More precisely, consider the mapping

(\bm{x}_{t},\bm{v})\mapsto\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{v}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{i}\bm{U}_{i}^{\top}\bm{v}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t}.

(6.4.27)

If we substitute $\bm{v}=\bm{v}_{y}$ for some $y\in[K]$ , we get

\displaystyle\begin{split}\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{v}_{y}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{i}\bm{U}_{i}^{\top}\bm{v}_{y}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t}&=\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{v}_{y}\right)}{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{v}_{y}\right)+K-1}\bm{U}_{y}\bm{U}_{y}^{\top}\bm{x}_{t}\\ &\quad+\sum_{k\neq y}\frac{1}{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{v}_{y}\right)+K-1}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t}.\end{split}

(6.4.28)

Now, because $\bm{x}_{t}=\alpha_{t}\bm{x}+\sigma_{t}\bm{g}$ , if the subspace dimension $P$ is sufficiently large—for example, if we consider a large-scale, asymptotic regime where $P,D\to\infty$ with their ratio $P/D$ converging to a fixed constant—we have for $t\approx 0$ that $\|\bm{x}_{t}\|_{2}$ is close to $\sqrt{P}$ , by the concentration of measure phenomenon¹¹¹¹11One of a handful of blessings of dimensionality—see [WM22].. Then by the argument in the previous paragraph, we have in this regime that for almost all realizations of $\bm{x}_{t}$ , the following approximation holds:

\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{v}_{y}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{i}\bm{U}_{i}^{\top}\bm{v}_{y}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t}\approx\bm{U}_{y}\bm{U}_{y}^{\top}\bm{x}_{t}.

(6.4.29)

This argument shows that the operator (6.4.27) is, with overwhelming probability, equal to the optimal class-conditional denoiser (6.4.18) for $y$ when $\bm{v}=\bm{v}_{y}$ ! In intuitive terms, at small noise levels $t\approx 0$ —corresponding to the structure-enforcing portion of the denoising process—plugging in the embedding for a given class $y$ to the second argument of the operator (6.4.27) leads the resulting function of $\bm{x}_{t}$ to well-approximate the optimal class-conditional denoiser (6.4.18) for $y$ . Moreover, it is evident that plugging in $\bm{v}=\bm{x}_{t}$ to the operator (6.4.27) yields (exactly) the optimal unconditional denoiser (6.4.19) for $\bm{x}_{t}$ . Thus, this operator provides a unified way to parameterize the constituent operators in the optimal denoiser for $\bm{x}$ within a single ‘network’: it is enough to add the output of an instantiation of (6.4.27) with input $(\bm{x}_{t},\bm{x}_{t})$ to an instantiation with input $(\bm{x}_{t},\bm{v}_{y}$ ). The resulting operator is a function of $(\bm{x}_{t},y)$ , and computationally, the subspaces $(\bm{U}_{k})_{k=1}^{K}$ and embeddings $y\mapsto\bm{v}_{y}$ become its learnable parameters. $\blacksquare$

Example 6.3 shows that in the special case of a low-rank mixture of Gaussians data distribution for $\bm{x}$ with incoherent components, operators of the form

(\bm{x}_{t},\bm{v})\mapsto\sum_{k=1}^{K}\frac{\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{v}\right)}{\sum_{i=1}^{K}\exp\left(\frac{1}{2t^{2}(1+t^{2})}\bm{x}_{t}^{\top}\bm{U}_{i}\bm{U}_{i}^{\top}\bm{v}\right)}\bm{U}_{k}\bm{U}_{k}^{\top}\bm{x}_{t}

(6.4.30)

provide a sufficiently rich class of operators to parameterize the MMSE-optimal denoiser for noisy observations $\bm{x}_{t}$ of $\bm{x}$ , in the setting of classifier-free guidance where one network is to be used to represent both the unconditional and class-conditional denoisers for $\bm{x}_{t}$ . For such operators, the auxiliary input $\bm{v}$ can be taken as either $\bm{x}_{t}$ or a suitable embedding of the class label $y\mapsto\bm{v}_{y}$ in order to realize such a denoiser. Based on the framework in Chapter 4, which develops deep network architectures suitable for transforming more general data distributions to structured representations using the low-rank mixture of Gaussians model as a primitive, it is natural to imagine that operators of the type (6.4.30) may be leveraged in denoisers for general data distributions $\bm{x}$ with low-dimensional geometrically-structured components that are sufficiently distinguishable (say, incoherent) from one another. The next section demonstrates that this is indeed the case.

6.4.2 Caption Conditioned Image Generation

In the previous subsection, we formulated denoisers for class-conditional denoising with classifier-free guidance, a ubiquitous practical methodology used in the largest-scale diffusion models, and showed how to parameterize them (in Example 6.3) in the special case of a low-rank Gaussian mixture model data distribution. One interesting byproduct of this example is that it highlights the crucial role of embeddings of the class label $y$ into a common space with the image $\bm{x}$ in order to provide a concise and unified scheme for parameterizing the optimal denoisers (conditional and unconditional). Below, we will describe an early such instantiation, which formed the basis for the original open-source Stable Diffusion implementation [RBL+22]. In this setting, the embedding and subsequent conditioning is performed not on a class label, but a text prompt, which describes the desired image content (Figure 6.13). We denote the raw tokenized text prompt as $\bm{Y}\in\mathbb{R}^{D_{\mathrm{text}}\times N}$ in this context, since it corresponds to a sequence of vectors—in Section 7.4, we describe the process of encoding a text sequence as a vector representation in detail.

Stable Diffusion follows the conditional generation methodology we outline in Section 6.4.1, with two key modifications: (i) The conditioning signal is a tokenized text prompt $\bm{Y}$ , rather than a class label; (ii) Image denoising is performed in “latent” space rather than on raw pixels, using a specialized, pretrained variational autoencoder pair $f:\mathbb{R}^{D_{\mathrm{img}}}\to\mathbb{R}^{d_{\mathrm{img}}}$ , $g:\mathbb{R}^{d_{\mathrm{img}}}\to\mathbb{R}^{D_{\mathrm{img}}}$ (see Section 5.1.4), where $f$ is the encoder and $g$ is the decoder. Subsequent model development has shown that point (ii) is an efficiency issue, rather than a core conceptual one, so we will not focus on it, other than to mention that it simply leads to the following straightforward modifications to the text-to-image pipeline sketched in Figure 6.13:

1.

At training time, the encoder $f:\bm{x}\mapsto\bm{z}$ is used to generate the denoising targets, and all denoising is performed on the encoded representations $\bm{z}_{t}\in\mathbb{R}^{d_{\mathrm{img}}}$ ;
2.

At generation time, sampling is performed on the representations $\hat{\bm{z}}_{t}$ , and the final image is generated by applying the decoder $g(\hat{\bm{z}}_{0})$ .

In contrast, issue (i) is essential, and the approach proposed to address it represents one of the lasting methodological innovations of [RBL+22]. In the context of the iterative conditional denoising framework we have developed in Section 6.4.1, this concerns the parameterization of the denoisers $\bar{\bm{z}}_{\theta}(t,\bm{z}_{t},\bm{Y}^{+})$ .¹²¹²12In the setting of text conditioning, the ‘augmented’ label $\bm{Y}^{+}$ , which is either the encoded text prompt or $\varnothing$ , denoting unconditional denoising, is often implemented by mapping $\varnothing$ to the empty string “”, then encoding this text prompt with the tokenizer as usual. This gives a simple, unified way to treat conditional and unconditional denoising with text conditioning. [RBL+22] implement text conditioning in the denoiser using a layer known as cross attention, inspired by the original encoder-decoder transformer architecture of [VSP+17]. Cross attention is implemented as follows. We let $\tau:\mathbb{R}^{D_{\mathrm{text}}\times N}\to\mathbb{R}^{d_{\mathrm{model}}\times N_{\mathrm{text}}}$ denote an encoding network for the text embeddings (often a causal transformer—see Section 7.4), and let $\psi:\mathbb{R}^{d_{\mathrm{img}}}\to\mathbb{R}^{d_{\mathrm{model}}\times N_{\mathrm{img}}}$ denote the mapping corresponding to one of the intermediate representations in the denoiser.¹³¹³13In practice, text-conditioned denoisers add cross attention layers at regular intervals within the forward pass of the denoiser, so $\psi$ should be seen as layer-dependent, in contrast to $\tau$ . See [RBL+22] for details. Here, $N_{\mathrm{text}}$ is the maximum tokenized text prompt length, and $N_{\mathrm{img}}$ roughly corresponds to the number of image channels (layer-dependent) in the representation, which is fixed if the input image resolution is fixed. Cross attention (with $K$ heads, and no bias) is defined as

\mathrm{MHCA}(\bm{z}_{t},\bm{Y}^{+})=\bm{U}_{\mathrm{out}}\begin{bmatrix}\operatorname{SA}([\bm{U}_{\mathrm{qry}}^{1}]^{\top}\psi(\bm{z}_{t}),[\bm{U}_{\mathrm{key}}^{1}]^{\top}\tau(\bm{Y}^{+}),[\bm{U}_{\mathrm{val}}^{1}]^{\top}\tau(\bm{Y}^{+}))\\ \vdots\\ \operatorname{SA}([\bm{U}_{\mathrm{qry}}^{K}]^{\top}\psi(\bm{z}_{t}),[\bm{U}_{\mathrm{key}}^{K}]^{\top}\tau(\bm{Y}^{+}),[\bm{U}_{\mathrm{val}}^{K}]^{\top}\tau(\bm{Y}^{+}))\end{bmatrix},

(6.4.31)

where $\mathrm{SA}$ denotes the ubiquitous self attention operation in the transformer (which we recall in detail in Chapter 7: see Equations 7.2.15 and 7.2.16), and $\bm{U}_{*}^{k}\in\mathbb{R}^{d_{\mathrm{model}}\times d_{\mathrm{attn}}}$ for $*\in\{\mathrm{qry},\mathrm{key},\mathrm{val}\}$ (as well as the output projection $\bm{U}_{\mathrm{out}}$ ) are the learnable parameters of the layer.

Notice that, by the definition of the self-attention operation, cross attention outputs linear combinations of the value-projected text embeddings weighted by correlations between the image features and the text embeddings. In the denoiser architecture used by [RBL+22], self-attention residual blocks in the denoiser architecture, applied to the image representation at the current layer and defined analogously to those in Equation 7.2.13 for the vision transformer, are followed by cross attention residual blocks of the form (6.4.31). Such a structure requires the text encoder $\tau$ to, in a certain sense, share some structure in its output with the image feature embedding $\psi$ : this can be enforced either by appropriate joint text-image pretraining (such as with CLIP [RKH+21]) or by joint training with the denoiser itself (which was proposed and demonstrated by [RBL+22], but has fallen out of favor due to high data and training costs for strong performance). Conceptually, this joint text-image embedding space and the cross attention layer itself bear a strong resemblance to the conditional mixture of Gaussians denoiser that we derived in the previous section (recall (6.4.27)), in the special case of a single token sequence. Deeper connections can be drawn in the multi-token setting following the rate reduction framework for deriving deep network architectures discussed in Chapter 4, and manifested in the derivation of the CRATE transformer-like architecture.

This same basic design has been further scaled to even larger model and dataset sizes, in particular in modern instantiations of Stable Diffusion [EKB+24], as well as in competing models such as FLUX.1 [LBB+25], Imagen [SCS+22], and DALL-E [RDN+22]. The conditioning mechanism of cross attention has also become ubiquitous in other applications, as in EgoAllo (Section 6.3.3) for conditioned pose generation and in Michelangelo [ZLC+23] for conditional 3D shape generation based on images or texts.

6.5 Conditional Inference with Measurement Self-Consistency

In this last section, we consider the more extreme, but actually ubiquitous, case for distribution learning in which we only have a set of observed samples $\bm{Y}=\{\bm{y}_{1},\ldots,\bm{y}_{N}\}$ of the data $\bm{x}$ , but no samples of $\bm{x}$ directly! In general, the observation $\bm{y}\in\mathbb{R}^{d}$ is of lower dimension than $\bm{x}\in\mathbb{R}^{D}$ . To make the problem well-defined, we do assume that the observation model between $\bm{y}$ and $\bm{x}$ is known to belong to a certain family of analytical models, denoted as $\bm{y}=h(\bm{x},\theta)+\bm{w}$ , with $\theta$ either known or not known.

Let us first try to understand the problem conceptually with the simple case when the measurement function $h$ is known and the observed $\bm{y}=h(\bm{x})+\bm{w}$ is informative about $\bm{x}$ . That is, we assume that $h$ is surjective from the space of $\bm{x}$ to that of $\bm{y}$ and the support of the distribution $\bm{y}_{0}=h(\bm{x}_{0})$ is low-dimensional. This typically requires that the extrinsic dimension $d$ of $\bm{y}$ is higher than the intrinsic dimension of the support of the distribution of $\bm{x}$ . Without loss of generality, we may assume that there exist functions:

F(\bm{x})=\bm{0},\quad G(\bm{y})=\bm{0}.

(6.5.1)

Notice that here we may assume that we know $G(\bm{y})$ but not $F(\bm{x})$ . Let $\mathcal{S}_{\bm{y}}\doteq\{\bm{y}\mid G(\bm{y})=\bm{0}\}$ be the support of $p(\bm{y})$ . In general, $h^{-1}(\mathcal{S}_{\bm{y}})=\{\bm{x}\mid G(h(\bm{x}))=\bm{0}\}$ is a superset of $\mathcal{S}_{\bm{x}}\doteq\{\bm{x}\mid F(\bm{x})=\bm{0}\}$ . That is, we have $h(\mathcal{S}_{\bm{x}})\subseteq\mathcal{S}_{\bm{y}}$ .

6.5.1 Linear Measurement Models

First, for simplicity, let us consider that the measurement is a linear function of the data $\bm{x}$ of interest:

\bm{y}=\bm{A}\bm{x}.

(6.5.2)

Here the matrix $\bm{A}\in\mathbb{R}^{m\times n}$ is of full row rank and $m$ is typically smaller than $n$ . We assume $\bm{A}$ is known for now. We are interested in how to learn the distribution of $\bm{x}$ from such measurements. Since we no longer have direct samples of $\bm{x}$ , we wonder whether we can still develop a denoiser for $\bm{x}$ with observations $\bm{y}$ . Let us consider the following diffusion process:

\bm{y}_{t}=\bm{y}_{0}+t\bm{g},\quad\bm{y}_{0}=\bm{A}(\bm{x}_{0}),

(6.5.3)

where $\bm{g}\sim\mathcal{N}(\bm{0},\bm{I})$ .

Without loss of generality, we assume $\bm{A}$ is of full row rank, i.e., under-determined. Let us define the corresponding process $\bm{x}_{t}$ as one that satisfies:

\bm{y}_{t}=\bm{A}\bm{x}_{t}.

(6.5.4)

From the denoising process of $\bm{y}_{t}$ , we have

\bm{y}_{t-s}\approx\bm{y}_{t}+st\nabla\log p_{t}(\bm{y}_{t}).

(6.5.5)

Then we have:

\bm{A}\bm{x}_{t-s}\approx\bm{A}\bm{x}_{t}+st\nabla\log p_{t}(\bm{A}\bm{x}_{t}),

(6.5.6)

for a small $s>0$ . So $\bm{x}_{t-s}$ and $\bm{x}_{t}$ need to satisfy:

\bm{A}(\bm{x}_{t-s}-\bm{x}_{t})\approx st\nabla\log p_{t}(\bm{A}\bm{x}_{t}).

(6.5.7)

Among all $\bm{x}_{t_{s}}$ that satisfy the above constraint, we arbitrarily choose the one that minimizes the distance $\|\bm{x}_{t-s}-\bm{x}_{t}\|_{2}^{2}$ . Therefore, we obtain a “denoising” process for $\bm{x}_{t}$ :

\bm{x}_{t-s}\approx\bm{x}_{t}+st\bm{A}^{\dagger}\nabla\log p_{t}(\bm{A}\bm{x}_{t}).

(6.5.8)

Notice that this process does not sample from the distribution of $\bm{x}_{t}$ . In particular, there are components of $\bm{x}$ in the null space/kernel of $\bm{A}$ that can never be recovered from observations. Thus more information is needed to recover the full distribution of $\bm{x}$ , strictly speaking. But this recovers the component of $\bm{x}$ that is orthogonal to the null space of $\bm{A}$ .

6.5.2 3D Visual Model from Calibrated Images

In practice, the measurement model is often nonlinear or only partially known. A typical problem of this kind is actually behind how we can learn a working model of the external world from the images perceived, say through our eyes, telescopes or microscopes. In particular, humans and animals are able to build a model of the 3D world (or 4D for a dynamical world) through a sequence of its 2D projections—a sequence of 2D images (or stereo image pairs). The mathematical or geometric model of the projection is generally known:

\bm{y}^{i}=h(\bm{x},\theta^{i})+\bm{w}^{i},

(6.5.9)

where $h(\cdot)$ represents a (perspective) projection of the 3D (or 4D) scene from a certain camera view at time $t_{i}$ to a 2D image (or a stereo pair) and $\bm{w}$ is some possibly additive small measurement noise. Figure 6.14 illustrates this relationship concretely, while Figure 6.15 illustrates the model problem in the abstract. A full exposition of geometry related to multiple 2D views of a 3D scene is beyond the scope of this book. Interested readers may refer to the book [MKS+04]. For now, all we need to proceed is that such projections are well understood and multiple images of a scene contain sufficient information about the scene.

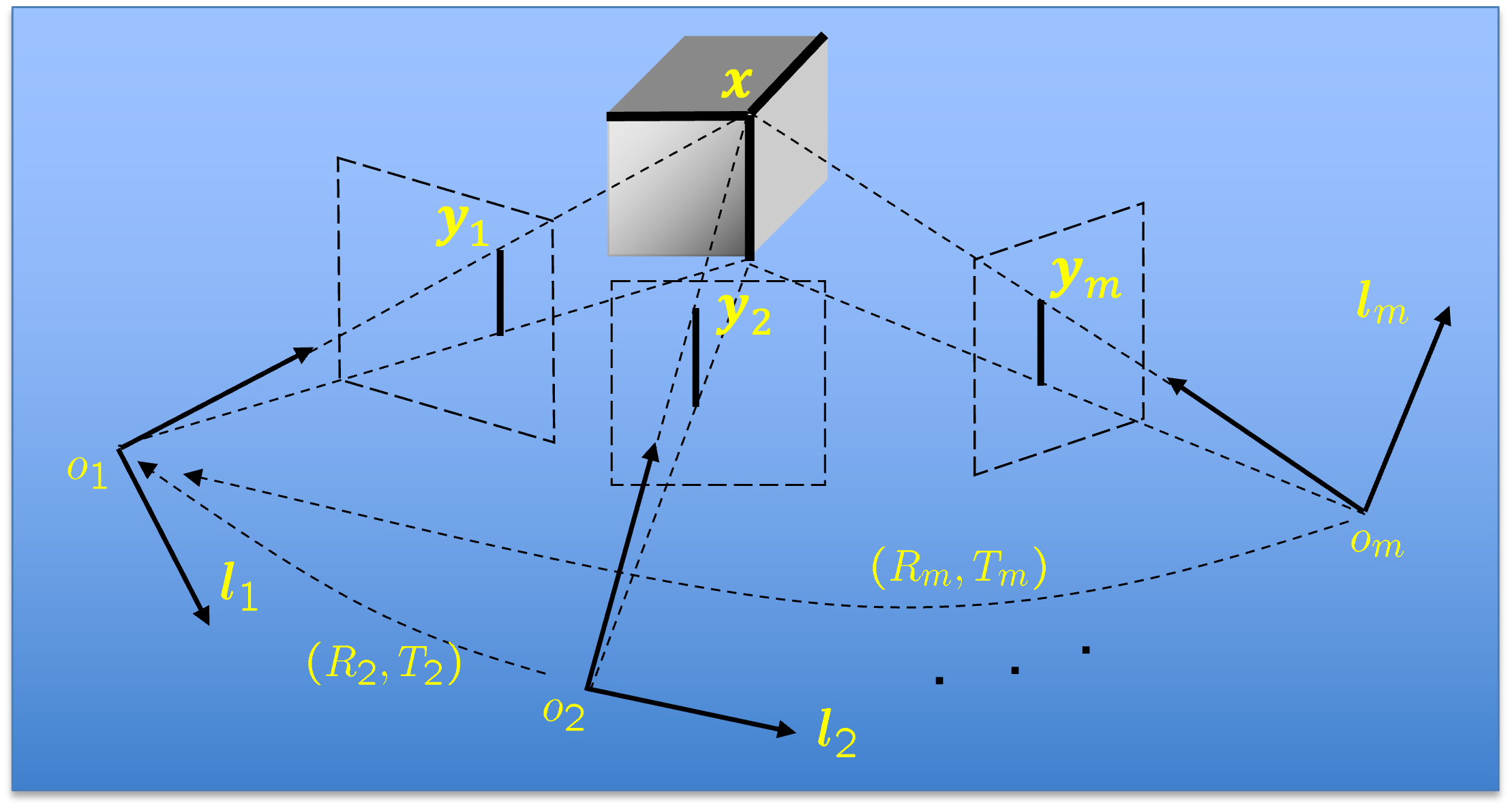
Figure 6.14 : Relationship between a 3D object/scene and its 2D projections. Here we illustrate the projection of a point 𝒙 \bm{x} bold_italic_x and a line intersecting the point. — Figure 6.14: Relationship between a 3D object/scene and its 2D projections. Here we illustrate the projection of a point $\bm{x}$ and a line intersecting the point.

Figure 6.15 : Inference with distributed measurements. We have a low-dimensional distribution 𝒙 \bm{x} bold_italic_x (here, similarly to Figure 6.1 , depicted as a union of two 2 2 2 -dimensional manifolds in ℝ 3 \mathbb{R}^{3} blackboard_R start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT ) and a measurement model 𝒚 i = h i ( 𝒙 ) + 𝒘 i \bm{y}^{i}=h^{i}(\bm{x})+\bm{w}^{i} bold_italic_y start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT = italic_h start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT ( bold_italic_x ) + bold_italic_w start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT . As before, we want to infer various properties of the conditional distribution of 𝒙 \bm{x} bold_italic_x given 𝒚 \bm{y} bold_italic_y , where 𝒚 \bm{y} bold_italic_y is the collection of all the measurements 𝒚 i \bm{y}^{i} bold_italic_y start_POSTSUPERSCRIPT italic_i end_POSTSUPERSCRIPT . — Figure 6.15: Inference with distributed measurements. We have a low-dimensional distribution $\bm{x}$ (here, similarly to Figure 6.1, depicted as a union of two $2$ -dimensional manifolds in $\mathbb{R}^{3}$ ) and a measurement model $\bm{y}^{i}=h^{i}(\bm{x})+\bm{w}^{i}$ . As before, we want to infer various properties of the conditional distribution of $\bm{x}$ given $\bm{y}$ , where $\bm{y}$ is the collection of all the measurements $\bm{y}^{i}$ .

In general, we would like to learn the distribution $p(\bm{x})$ of the 3D (or 4D) world scene $\bm{x}$ ¹⁴¹⁴14Here by abuse of notation, we use $\bm{x}$ to represent either a point in 3D or a sample of an entire 3D object or a scene that consists of many points. from the perceived 2D images of the world so far. The primary function of such a (visual) world model is to allow us to recognize places where we had been before or predict what the current scene would look like in a future time at a new viewpoint.

Let us first examine the special but important case of stereo vision. In this case, we have two calibrated views of the 3D scene $\bm{x}$ :

\bm{y}^{0}=h(\bm{x},\theta^{0})+\bm{w}^{0},\quad\bm{y}^{1}=h(\bm{x},\theta^{1})+\bm{w}^{1},

(6.5.10)

where parameters $\theta_{0}$ and $\theta_{1}$ for the view poses can be assumed to be known. $\bm{y}^{0}$ and $\bm{y}^{1}$ are two 2D-projections of the 3D scene $\bm{x}$ . We may also assume that they have the same marginal distribution $p(\bm{y})$ and we have learned a diffusion and denoising model for it. That is, we know the denoiser:

\mathbb{E}[\bm{y}\mid\bm{y}_{t}=\bm{\nu}]=\bm{\nu}+t^{2}\nabla_{\bm{\nu}}\log p_{t}(\bm{\nu}).

(6.5.11)

Or, furthermore, we may assume that we have a sufficient number of samples of stereo pairs $(\bm{y}^{0},\bm{y}^{1})$ and have also learned the joint distribution of the pairs. By a little abuse of notation, we also use $\bm{y}=h(\bm{x})$ to indicate the pair $\bm{y}=(\bm{y}^{0},\bm{y}^{1})$ and $p(\bm{y})$ as the learned probability distribution of the pair (say via a denoiser as above).

The main question now is: How to learn (a representation for) the distribution of the 3D scene $\bm{x}$ from its two projections with known relationships? People might question the rationale for doing this: why is this necessary if the function $h(\cdot)$ is largely invertible? That is, the observation $\bm{y}$ can largely determine the unknown $\bm{x}$ , which is kind of the case for stereo—in general, two (calibrated) images contain sufficient information about the scene depth, from the given vantage point. However, 2D images are far from the most compact representation of the 3D scene as the same scene can produce infinitely many (highly correlated) 2D images or image pairs. In fact, a good representation of a 3D scene should be invariant to the viewpoint. Hence, a correct representation of the distribution of 3D scenes should be much more compact and structured than the distribution of 2D images, stereo pairs, or image-depth pairs.

Consider the (inverse) denoising process for the diffusion: $\bm{y}_{t}=\bm{y}+t\bm{g}$ in (6.5.11), where $\bm{g}$ is standard Gaussian. From the denoising process of (6.5.11), we have

\bm{y}_{t-s}=\bm{y}_{t}+st\nabla_{\bm{y}}\log p_{t}(\bm{y}_{t}).

(6.5.12)

We try to find a corresponding “denoising” process of $\bm{x}_{t}$ such that $\bm{x}$ is related to $y$ as:

\bm{y}=h(\bm{x}).

(6.5.13)

Then we have:

h(\bm{x}_{t-s})\approx h(\bm{x}_{t})+st\nabla_{\bm{y}}\log p_{t}(h(\bm{x}_{t})),

(6.5.14)

for a small $s>0$ . Suppose $\bm{x}_{t-s}=\bm{x}_{t}+s\bm{v}$ for some vector $\bm{v}$ and small increment $s$ . We have

h(\bm{x}_{t-s})\approx h(\bm{x}_{t})+\frac{\partial h}{\partial\bm{x}}(\bm{x}_{t})\cdot\bm{v}s\doteq h(\bm{x}_{t})+\bm{A}(\bm{x}_{t})\bm{v}s.

(6.5.15)

Hence, we have

\bm{A}(\bm{x}_{t})\bm{v}=t\nabla_{\bm{y}}\log p_{t}(h(\bm{x}_{t})).

(6.5.16)

Geometrically the vector $\bm{v}$ in the domain of $\bm{x}$ can be viewed as the pullback of the vector field $t\nabla\log p_{t}(\bm{y})$ under the map $\bm{y}=h(\bm{x})$ . In general, as before, we may (arbitrarily) choose $\bm{v}$ to be the minimum 2-norm vector that satisfies the pullback relationship. Hence, we can express $\hat{\bm{x}}_{t-s}$ approximately as:

\hat{\bm{x}}_{t-s}\approx\bm{x}_{t}+st\bm{A}(\bm{x}_{t})^{\dagger}\nabla_{\bm{y}}\log p_{t}(h(\bm{x}_{t})).

(6.5.17)

Remark 6.2 (Parallel Sensing and Distributed Denoising.).

There is something very interesting about the above equation (6.5.17). It seems to suggest we could try to learn the distribution of $\bm{x}$ through a process that is coupled with (many of) its (partial) observations:

\bm{y}^{i}=h^{i}(\bm{x})+\bm{w}^{i},i=1,\ldots,K.

(6.5.18)

In this case, we obtain a set of equations that the vector field $\bm{v}$ in the domain of $\bm{x}$ should satisfy:

\bm{A}^{i}(\bm{x}_{t})\bm{v}=t\nabla_{\bm{y}^{i}}\log p_{t}(h^{i}(\bm{x}_{t})),

(6.5.19)

where $\bm{A}^{i}(\bm{x}_{t})=\frac{\partial h^{i}}{\partial\bm{x}}(\bm{x}_{t})$ . The final $\bm{v}$ can be chosen as a “centralized” solution that satisfies all the above equations, or it could be chosen as a certain (stochastically) “aggregated” version of all $\bm{v}^{i}$ :

\bm{v}^{i}=t\bm{A}^{i}(\bm{x}_{t})^{\dagger}\big{[}\nabla_{\bm{y}^{i}}\log p_{t}(h^{i}(\bm{x}_{t}))\big{]},\quad i=1,\ldots,K,

(6.5.20)

that are computed in a parallel and distributed fashion? An open question here is exactly what the so-defined “denoising” process for $\bm{x}_{t}$ converges to, even in the linear measurement model case. When would it converge to a distribution that has the same low-dimensional support as the original $\bm{x}_{0}$ , as $\bm{y}_{t}$ converges to $\bm{y}=h(\bm{x}_{0})$ ?

Visual World Model from Uncalibrated Image Sequences

In the above derivation, we have assumed that the measurement model $h(\cdot)$ is fully known. In the case of stereo vision, this is rather reasonable as the relative pose (and calibration) of the two camera views (or two eyes¹⁵¹⁵15The relative pose of our two eyes is well known to our brain.) is usually known in advance. Hence, through the stereo image pairs, in principle we should be able to learn the distribution of 3D scenes, at least the ego-centric distribution of 3D scenes. However, the low-dimensional structures of the so-called learned distribution contain variation caused by changing the viewpoints. That is, the appearance of the stereo images varies when we change our viewpoints with respect to the same 3D scene. For many practical vision tasks (such as localization and navigation), it is important that we can decouple this variation of viewpoints from an invariant representation of (the distribution of) 3D scenes.

Remark 6.3.

Note that the above goal aligns well with Klein’s Erlangen Program for modern geometry, which is to study invariants of a manifold under a group of transformations. Here, we may view the manifold of interest as the distribution of ego-centric representations of 3D scenes. We have learned that it admits a group of three-dimensional rigid-body motion acting on it. It is remarkable that our brain has learned to effectively decouple such transformations from the observed 3D world.

Notice that we have studied learning representations that are invariant to translation and rotation in a limited setting in Chapter 4. We know that the associated compression operators take the necessary form of (multi-channel) convolutions, hence leading to the (deep) convolutional neural networks. Nevertheless, operators that are associated with compression or denoising that are invariant to more general transformation groups remain elusive to characterize [CW16a]. For the 3D Vision problem in its most general setting, we know the change of our viewpoints can be well modeled as a rigid-body motion. However, the exact relative motion of our eyes between different viewpoints is usually not known. More generally, there could also be objects (e.g., cars, humans, hands) moving in the scene and we normally do not know their motion either. How can we generalize the problem of learning the distribution of 3D scenes with calibrated stereo pairs to such more general settings? More precisely, we want to learn a compact representation $\bm{x}$ of the 3D scenes that is invariant to the camera/eye motions. Once such a representation is learned, we could sample and generate a 3D scene and render images or stereo pairs from arbitrary poses.

To this end, note that we can model a sequence of stereo pairs as:

\bm{y}^{k}=h(\bm{x}^{k},\theta^{k}),\quad k=1,\ldots,K,

(6.5.21)

where $h(\cdot)$ represents the projection map from 3D to 2D. $\theta^{k}$ denotes the rigid-body motion parameters of the $k$ th view, with respect to some canonical frame in the world. $\bm{x}^{k}$ represents the 3D scene at time $k$ . If the scene is static, $\bm{x}^{k}$ should all be the same $\bm{x}^{k}=\bm{x}$ . To simplify the notation, we may denote the set of $k$ equations as one:

\bm{Y}=H(\bm{x},\Theta).

(6.5.22)

We may assume that we are given many samples of such stereo image sequences $\{\bm{Y}_{i}\}$ . The problem is how to recover the associated motion sequence $\{\Theta_{i}\}$ and learn the distribution of the scene $\bm{x}$ (that is invariant to the motion). To the best of our knowledge, this remains an open challenging problem, probably as the final frontier for the 3D Vision problem.

6.6 Summary and Notes

Measurement matching without clean samples.

In our development of conditional sampling, we considered measurement matching under an observation model (6.3.9), where we assume that we have paired data $(\bm{x},\bm{y})$ —i.e., ground truth for each observation $\bm{y}$ . In many practically relevant inverse problems, this is not the case: one of the most fundamental examples is in the context of compressed sensing, which we recalled in Chapter 2, where we need to reconstruct $\bm{x}$ from $\bm{y}$ using prior knowledge about $\bm{x}$ (i.e., sparsity). In the setting of denoising-diffusion, we have access to an implicit prior for $\bm{x}$ via the learned denoisers $\bar{\bm{x}}_{\theta}(t,\bm{\xi})$ . Can we still perform conditional sampling without access to ground truth samples $\bm{x}$ ?

For intuition as to why this might be possible, we recall a classical example from statistics known as Stein’s unbiased risk estimator (SURE). Under an observation model $\bm{x}_{t}=\bm{x}+t\bm{g}$ with $\bm{g}\sim\mathcal{N}(\mathbf{0},\bm{I})$ and $t>0$ , it turns out that for any weakly differentiable $f:\mathbb{R}^{D}\to\mathbb{R}^{D}$ ,

\mathbb{E}_{\bm{g}}\left[\left\|\bm{x}-f(\bm{x}+t\bm{g})\right\|_{2}^{2}\right]=\mathbb{E}_{\bm{g}}\left[\left\|\bm{x}+t\bm{g}-f(\bm{x}+t\bm{g})\right\|_{2}^{2}+2t^{2}\nabla\cdot f(\bm{x}+t\bm{g})\right]-t^{2}D,

(6.6.1)

where $\nabla\cdot$ denotes the divergence operator:

\nabla\cdot f=\sum_{i=1}^{D}\partial_{i}f_{i}.

The $\bm{x}$ -dependent part of the RHS of Equation 6.6.1 is called Stein’s unbiased risk estimator (SURE). If we take expectations over $\bm{x}$ in Equation 6.6.1, note that the RHS can be written as an expectation with respect to $\bm{x}_{t}$ —in particular, the mean-squared error of any denoiser $f$ can be estimated solely from noisy samples! This remarkable fact, in refined forms, constitutes the basis for many practical techniques for performing image restoration, denoising-diffusion, etc. using only noisy data: notable examples include the “noise2noise” paradigm [LMH+18] and Ambient Diffusion [DSD+23].

As a fun aside, we point out that Equation 6.6.1 leads to an alternate proof of Tweedie’s formula (Theorem 3.3). At a high level, one takes expectations over $\bm{x}$ and expresses the main part of the RHS of Equation 6.6.1 equivalently, via integration by parts, as

\mathbb{E}_{\bm{x}_{t}}\left[\left\|\bm{x}_{t}-f(\bm{x}_{t})\right\|_{2}^{2}+2t^{2}\nabla\cdot f(\bm{x}_{t})\right]=\mathbb{E}_{\bm{x}_{t}}\left[\left\|\bm{x}_{t}-f(\bm{x}_{t})\right\|_{2}^{2}\right]-2t^{2}\int\left\langle\nabla p_{\bm{x}_{t}}(\bm{\xi}),f(\bm{\xi})\right\rangle\mathrm{d}\bm{\xi}.

(6.6.2)

This is a quadratic function of $f$ , and formally taking derivatives gives that the optimal $f$ satisfies Tweedie’s formula (Theorem 3.3). This argument can be made rigorous using basic ideas from the calculus of variations.

Corrections to the Diffusion Posterior Sampling (DPS) approximation.

In Example 6.2 and in particular in Figure 6.9, we pointed out a limitation of the DPS approximation Equation 6.3.26 at small levels of measurement noise. This limitation is well-understood, and a principled approach to ameliorating it has been proposed by Rozet et al. [RAL+24]. The approach involves incorporating an additional estimate for the variance of the noisy posterior $p_{\bm{x}\mid\bm{x}_{t}}$ to Equation 6.3.26—we refer to the paper for details. Natural estimates for the posterior variance are slightly less scalable than DPS itself due to the need to invert an affine transformation of the Jacobian of the posterior denoiser $\mathbb{E}[\bm{x}\mid\bm{x}_{t}=\bm{\xi}]$ (a large matrix). This is done relatively efficiently by Rozet et al. [RAL+24] using automatic differentiation and an approximation for the inverse based on conjugate gradients. It seems that it should be possible to improve further over this approach (say, using classical ideas from second-order optimization).

More about measurement matching and diffusion models for inverse problems.

Diffusion models have become an extremely popular tool for solving inverse problems arising in scientific applications. Many more methods beyond the simple DPS algorithm we have presented in Algorithm 6.1 have been developed and continue to be developed, as the area is evolving rapidly. Popular and performant classes of approaches beyond DPS, which we have presented due to its generality, include variable splitting approaches like DAPS [ZCB+24], which allow for specific measurement constraints to be enforced much more strongly than in DPS, and exact approaches that can avoid the use of approximations as in DPS, such as TDS [WTN+23]. For more on this area, we recommend [ZCZ+25], which functions simultaneously as a survey and a benchmark of several popular methods on specific scientific inverse problem datasets.

6.7 Exercises and Extensions

Exercise 6.1 (Posterior Variance Correction to DPS).

1.

Using the code provided in the book GitHub for implementing Figure 6.9, implement the posterior variance correction proposed by [RAL+24].
2.

Verify that it ameliorates the posterior collapse at low noise variance issue observed in Figure 6.9.
3.

Discuss any issues of sampling correctness that are retained or introduced by the corrected method, as well as its efficiency, relative to diffusion posterior sampling (DPS).

Exercise 6.2 (Conditional Sampling on MNIST).

1.

Train a simple classifier for the MNIST dataset, using an architecture of your choice. Additionally train a denoiser suitable for use in conditional sampling (Algorithm 6.2, since this denoiser can be used for unconditional denoising as well).
2.

Integrate the classifier into a conditional sampler based on classifier guidance, as described in the first part of Section 6.4.1. Evaluate the resulting samples in terms of faithfulness to the conditioning class (visually; in terms of nearest neighbor; in terms of the output of the classifier).
3.

Integrate the classifier into a conditional sampler based on classifier-free guidance, as described in Section 6.4.1 and Algorithm 6.2. Perform the same evaluation as in the previous step, and compare the results.
4.

Repeat the experiment on the CIFAR-10 dataset.