Chapter 5 Consistent and Self-Consistent Representations
“Everything should be made as simple as possible, but not any simpler.”
– Albert Einstein
In the past chapters, we have established a basic fact that the fundamental goal of learning is to learn a data distribution with low-dimensional support and transform it into a compact and structured representation. Such a representation reveals intrinsic low-dimensional structures of the data distribution and facilitates subsequent tasks such as classification and generation.
A fundamental approach to learning a good representation of such a distribution is through compression. To make the goal of compression measurable and computable, it can be done explicitly by learning a coding scheme that minimizes the coding rate (entropy) or maximizes the information gain (coding rate reduction). In this context, the fundamental role of a deep neural network is to realize a certain iterative optimization algorithm that incrementally optimizes the learned representations in terms of those measures:
| (5.0.1) |
In the preceding chapter, we have shown that main architectural characteristics of almost all popular deep networks (ResNet, CNN, and Transformer) can be derived and interpreted from this perspective.
However, when we try to achieve a certain objective through optimization, there is no guarantee that the solution found in the end by incremental optimization is the correct solution. In fact, even if the optimization process manages to find the globally optimal solution , there is no guarantee that the solution corresponds to a complete representation of the data distribution.111This could be due to many reasons: for example, the data available for learning the distribution might not be sufficient, or the formulation of the optimization program fails to consider some additional constraints or conditions. Therefore, an outstanding question is: how can we ensure that the learned representation of the data distribution is correct or good enough?
Of course, the only way to verify this is to see whether there exists a decoding map, say , that can decode the learned representation to reproduce the original data (distribution) well enough:
| (5.0.2) |
in terms of some measure of similarity:
| (5.0.3) |
This leads to the concept of consistent representation. As we have briefly alluded to in Chapter 1 (see Figure 1.23), autoencoding, which integrates the encoding and decoding processes, is a natural framework for learning such a representation. We have studied some important special cases in Chapter 2. In this chapter, Section 5.1, we will study how to extend autoencoding to more general classes of distributions by enforcing the consistency between and .
In many practical and natural learning scenarios, it can be difficult or even impossible to compare distributions of the data and . We are left with the only option of comparing the learned feature with its image under the encoder :
| (5.0.4) |
This leads to the notion of a self-consistent representation. In Section 5.2, we will study when and how we can learn a consistent representation by enforcing the self-consistency between and only through a closed-loop transcription framework.
Furthermore, in many practical and natural learning scenarios, we normally do not have sufficient samples of the data distribution all available at once. For example, animals and humans develop their visual memory by continuously taking in increments of observations throughout their lives. In Section 5.3, we will study how to extend the closed-loop transcription framework to learn a self-consistent representation in a continuous learning setting.
Of course, a fundamental motivation for why we ever want to identify the low-dimensional structures in a data distribution and find a good representation is to make it easy to use the data for various tasks of intelligence, such as classification, completion, and prediction. Therefore, the resulting joint representation must be structured in such a way that is best suited for these tasks. In the next chapter, we will see how the learned representation can be structured to facilitate conditioned completion or generation tasks.
5.1 Learning Consistent Representations
Here we give a formal definition of consistent representations, which are closely related to the concept of autoencoding.
Definition 5.1 (Consistent Representations).
Given data , a consistent representation is a pair of functions , such that the features are compact and structured, and the autoencoding
| (5.1.1) |
is close to according to either the following two measures:
-
1.
We say that it is sample-wise consistent if in a certain norm with high probability.
-
2.
We say that the representation is distributionally consistent if .
Astute readers may have noticed that if we do not impose certain requirements on the representation sought, the above problem has a trivial solution: one may simply choose the functions and to be the identity map! Hence, the true purpose of seeking an autoencoding is to ensure that the so obtained is both more compact and more structured than . First, for compactness, should better reveal the intrinsic low-dimensionality of . Therefore, the representation should maximize a certain information gain, say, measured by the rate reduction
| (5.1.2) |
introduced in Section 3.4.2. Second, the main purpose of learning a good representation of the data distribution is to facilitate tasks that exploit the low-dimensionality of its distribution. Hence, the distribution of should be better structured. For example, the distribution of is piecewise linear or Gaussian, and its components are largely incoherent or independent. These independent components can represent different clusters or classes and can also easily be used as conditions for decoding the corresponding data .
From the definition of consistent representation, it is required that the representation be sufficient to recover the original data distribution to some degree of accuracy. For sample-wise consistency, a typical choice is to minimize the expected reconstruction error:
| (5.1.3) |
For consistency in distribution, a typical choice is to minimize a certain distributional distance such as the KL divergence222Note that for distributions without common support, which is typical for degenerate distributions, KL divergence may not even be well-defined. In fact, much of the distribution learning literature is trying to address this technical difficulty by replacing or approximating it with something well-defined and efficiently computable.:
| (5.1.4) |
Hence, computation aside, when we seek a good autoencoding for a data distribution , conceptually we try to find an encoder and decoder such that
| (5.1.5) |
For the rest of this chapter, we will study how to solve such autoencoding problems under different conditions, from simple and ideal cases to increasingly more challenging and realistic conditions.
5.1.1 Linear Autoencoding via PCA
According to [Bal11], the phrase “autoencoder” was first introduced by Hinton and Rumelhart [RHW86] so that a deep representation could be learned via back propagation (BP) in a self-supervised fashion—reconstructing the original data is the self-supervising task. However, the very same concept of seeking a compact and consistent representation has its roots in many classic studies. As we have already seen in Chapter 2, the classical PCA, ICA, and sparse dictionary learning all share a similar goal. The only difference is that when the underlying data distribution is simple (linear and independent), the encoding or decoding mappings become easy to represent and learn: they do not need to be deep and often can be computed in closed form or with an explicit algorithm.
It is instructive to see how the notion of consistency we have defined plays out in the simple case of PCA: here, the consistent encoding and decoding mappings are given by a single-layer linear transform:
| (5.1.6) |
where typically with . Hence represents a projection from a higher-dimensional space to a lower one , as illustrated in Figure 5.1.
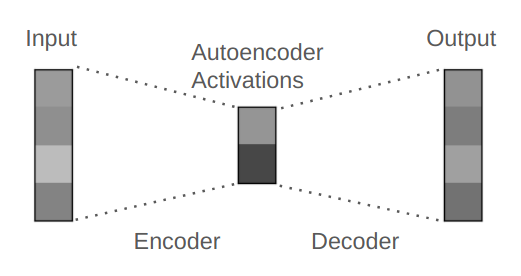
As we saw in Chapter 2, when the distribution of is indeed supported on a low-dimensional subspace , the compactness of the representation produced by is a direct consequence of correctly estimating (and enforcing) the dimension of this subspace. Finally, recall that gradient descent on the reconstruction criterion exactly yields these sample-wise consistent mappings: indeed, the optimal solution to the problem
| (5.1.7) |
precisely coincides with when the dimension of the representation is sufficiently large. In this case, we obtain sample-wise consistency for free, since this guarantees that . Notice that in the case of PCA, the rate reduction term in (5.1.5) becomes void as the regularization on the representation sought is explicit: It spans the entire subspace of lower dimension333One may view in this case..
Online PCA.
Notice that in the above construction, the linear transform used for encoding and decoding is computed “offline” from all the input data beforehand. One question is whether this transform can be learned “online” as the input data comes in order. This question was answered by the work of Oja in 1982 [Oja82].
Example 5.1 (Normalized Hebbian learning scheme for PCA).
Consider a sequence of i.i.d. random vectors with covariance . Let and define the response of an input vector against a weight vector to be their inner product:
| (5.1.8) |
and we update the weight vector according to the following scheme:
| (5.1.9) |
for some small gain . This update scheme can be viewed as a normalized Hebbian scheme, in which the weights of connections between neurons become stronger if (products of) both the input and output are strong. One may view the vector of weights as “learned” based on a form of feedback from the output . Then, under reasonable assumptions, Oja [Oja82] has shown that converges to the eigenvector associated with the largest eigenvalue of .
The normalized Hebbian scheme (5.1.9) can be interpreted as a first-order approximation to a stochastic projected gradient descent scheme on the objective of the problem (5.1.7) (with batch size , and with the number of columns of equal to ) as long as , which is maintained by the projection operation in (5.1.9). It is worth keeping its existence in the back of one’s mind, both as a proof of correctness for the use of stochastic gradient methods for optimizing reconstruction costs such as (5.1.7), and for its suggestion that simpler algorithms than (end-to-end) back propagation can succeed in learning consistent autoencoders.
5.1.2 Nonlinear PCA and Autoencoding
Of course, one should expect that things will no longer be so simple when we deal with more complex distributions whose underlying low-dimensional structures are nonlinear.
Data on a Nonlinear Submanifold.
So, to move beyond the linear structure addressed by PCA, we may assume that the data distribution lies on a (smooth) submanifold . The intrinsic dimension of the submanifold, say , is typically much lower than the dimension of the ambient space . From this geometric perspective, we typically want to find a nonlinear mapping such that the resulting manifold is flattened, as illustrated by the example shown in Figure 5.2. The resulting feature -space is typically more compact (of lower-dimension) than the -space, and the manifold is flat. From the statistical perspective, which is complementary to the geometric perspective but distinct in general, we may also want to ensure that the data distribution on is mapped to a sufficiently regular distribution, say a Gaussian or uniform distribution (with very low-dimensional support), in the -space. These two properties ensure that sampling and interpolation in the -space are as easy as possible, and they are mathematical formalizations of the desirable notions of compact and structured features in the low-dimensional manifold model for the data distribution. In general, the problem of learning such an autoencoding mapping for this class of data distributions is known as nonlinear principal component analysis (NLPCA).
A Classical Attempt via a Two-Layer Network.
As we have seen above, in the case of PCA, a single-layer linear neural network is sufficient. That is no longer the case for NLPCA. In 1991, Kramer [Kra91] proposed to solve NLPCA by using a two-layer neural network to represent the encoder mapping (or its inverse ) based on the universal representation property of two-layer networks with sigmoid activation:
| (5.1.10) |
where is the sigmoid function:
| (5.1.11) |
Cybenko [Cyb89] showed that functions of the above form (with enough hidden nodes) can approximate any smooth nonlinear function, say the encoder , to an arbitrary precision. In particular, they can represent the flattening and reconstruction maps for data distributions supported on unions of low-dimensional manifolds, as in Figure 5.2. The overall architecture of the original networks proposed by Kramer is illustrated in Figure 5.3.
![Figure 5.3 : Nonlinear PCA by autoassociative neural networks of depth two for both the encoding and decoding mappings, suggested by Kramer [ Kra91 ] .](chapters/chapter5/figs/kramer1991nonlinearPCA.png)
Unfortunately, unlike the case of PCA above, there is in general no closed-form learning scheme for the parameters of these networks. Hence it was proposed to train the network via back propagation with the supervision of reconstruction error:
| (5.1.12) |
Compared to the simple case of PCA, we utilize the same reconstruction objective for learning, but a far more complex nonlinear class of models for parameterizing and learning the encoder and decoder. Although universal approximation properties such as Cybenko’s suggest that in principle learning consistent autoencoders via this framework is possible—because for any random sample of data, given enough parameters, such autoencoding pairs exist—one often finds it highly nontrivial to find them using gradient descent. Moreover, to obtain a sufficiently informative reconstruction objective and model for the distribution of high-dimensional real-world data such as images, the required number of samples and hidden nodes can be huge. In addition, as a measure of the compactness of the learned representation, the (lower) dimension of for the bottleneck layer is often chosen heuristically.444In the later work [HZ93], Hinton et al. suggested to use the minimum description length (MDL) principle to promote the compactness of the learned coding scheme, in a spirit very similar to the rate distortion measure introduced in this book.
Manifold Flattening via a Deeper Network.
Based on the modern practice of deep networks, such classical shallow and wide network architectures are known to be rather difficult to train effectively and efficiently via back propagation (BP), partly due to the vanishing gradient of the sigmoid function. Hence, the modern practice normally suggests further decomposing the nonlinear transform (or ) into a composition of many more layers of simpler transforms, resulting in a deeper network architecture [HS06], as illustrated in Figure 5.4. In the modern context, further elaborations over the basic reconstruction cost (5.1.12) also prove necessary to achieve good performance on complex real-world data distributions such as images.
In light of universal approximation theorems such as Cybenko’s, one may initially wonder why, conceptually, deeper autoencoders should be preferred over shallow ones. From purely an expressivity perspective, we can understand this phenomenon through a geometric angle related to the task of flattening the nonlinear manifold on which our hypothesized data distribution is supported. A purely constructive approach to flattening the manifold proceeds incrementally, in parallel to what we have seen in Chapters 3 and 4 with the interaction between diffusion, denoising, and compression. In the geometric setting, the incremental flattening process corresponding to takes the form of transforming a neighborhood of one point of the manifold to be closer to a flat manifold (i.e., a subspace), and enforcing local consistency with the rest of the data samples; the corresponding incremental operation in the decoder, , undoes this transformation. This procedure precisely incorporates curvature information about the underlying manifold, which is estimated from data samples. Given enough samples from the manifold and a careful instantiation of this conceptual process, it is possible to implement this procedure as a computational procedure that verifiably flattens nonlinear manifolds in a white-box fashion [PPR+24]. However, the approach is limited in its applicability to high-dimensional data distributions such as images due to unfavorable scalability, motivating the development of more flexible methods to incremental autoencoding.
5.1.3 Sparse Autoencoding
In the above autoencoding schemes, the dimension of the feature space is typically chosen to be much lower than that of the original data space in order to explicitly enforce or promote the learned representation to be low-dimensional. However, in practice, we normally do not know the intrinsic dimension of the data distribution. Hence, the choice of the feature space dimension for autoencoding is often done empirically. In more general situations, the data distribution can be a mixture of a few low-dimensional subspaces or submanifolds. In these cases, it is no longer feasible to enforce a single low-dimensional space for all features together.
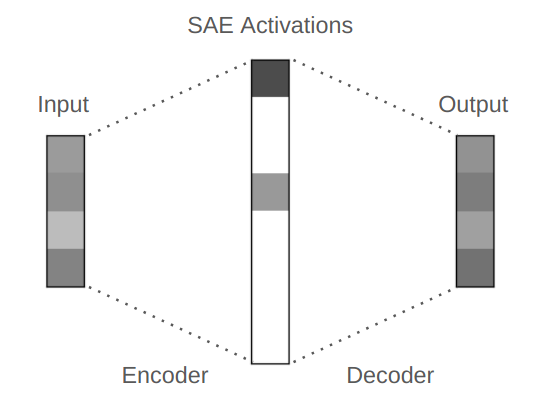
The sparse autoencoder is meant to resolve some of these limitations. In particular, the dimension of the feature space can be equal to or even higher than that of the data space, as illustrated in Figure 5.5. However, the features are required to be highly sparse in the feature space. So if we impose sparsity as a measure of parsimony in addition to rate reduction in the objective (5.1.5), we obtain a new objective for sparse autoencoding:
| (5.1.13) |
where the -“norm” is known to promote sparsity. This is very similar to the sparse rate reduction objective (4.2.4) which we used in the previous Chapter 4 to derive the white-box CRATE architecture.
5.1.4 Variational Autoencoding
In the classical conception of autoencoding, following Hinton and Rumelhart [RHW86], the data distribution plays a very minor role in the formulation, despite its centrality to the representation we ultimately learn. Indeed, in the naive framework, one hopes that by training a deep network to reconstruct samples from the data distribution with a suitably configured bottleneck for the representation , the learned encoders and will naturally end up corresponding to a compact and structured feature representation for the data. This is rarely the case in practice. An improved, more modern methodology for autoencoding that still finds significant application to this day is variational autoencoding [KW13, KW19]. We will see how this framework, which trains a variational autoencoder (VAE) derived through probabilistic modeling considerations, both generalizes the classical autoencoder training (via minimization of the reconstruction loss), and stabilizes it with appropriate regularization. Later, we will see how to go further and go beyond the black-box nature of the deep networks used to represent the encoding and decoding mappings and .
Probabilistic Perspective on Autoencoding
In the manifold model for the data distribution, the key mathematical objects are the support of the data distribution, namely the manifold , and the density of the data on the support, say . When we formulate autoencoding from the probabilistic perspective, we often think of the high-dimensional input as having a density with support on ; one can think of adding a very small amount of noise to the (degenerate) distribution supported on the manifold to obtain this density , in line with our denoising-diffusion constructions in Chapter 3. Then the goal of generative probabilistic modeling is to learn the density from samples , say from a class of models parameterized by . As we have recalled in Chapter 3, a classical approach to achieving this is via maximum likelihood estimation:
For certain representative classes of data distributions and sufficiently expressive classes of models , even simpler learning problems than maximum likelihood estimation are known to be statistically hard [YB99]. Hence it is desirable to exploit the knowledge that has low-dimensional structure by seeking to factor the distribution according to a low-dimensional “latent” variable model . Indeed, by conditioning we may write , and
Classically, our model for the data distribution corresponds to a choice of the latent distribution and the conditional distribution . Even so, computing the model for the data distribution from these latent distributions is intractable except in special cases, analogous to those we have studied in Chapter 2. By the same token, computing the posterior from data, allowing us to encode samples to their corresponding latents, is generally intractable. There is hence a trade-off between the expressivity of our generative model, its computational tractability, and the accuracy of any approximations we make to the underlying probabilistic framework for the sake of computational tractability. In navigating this trade-off, one also needs a flexible computational approach for learning the model parameters from data, analogous to the maximum likelihood objective.
In the variational autoencoding framework, we navigate this trade-off through three key insights:
-
1.
We posit simple distributions for and conditional on , but make their parameters depend in a highly flexible way on the input data (where relevant) using deep networks.
-
2.
We replace the posterior , used for encoding and whose form is implied (by Bayes rule) by our modeling choices for , with a tractable approximation , which has its own parameters .
-
3.
We jointly learn and via maximizing a tractable lower bound for the likelihood , known as the evidence lower bound (ELBO).
We will focus on the most useful instantiation of the VAE framework in practice, namely where the prior and the conditional are both Gaussian. Namely, we use the following Gaussian distributions:
where are deep networks with parameters , which correspond to the decoder in the autoencoder. Similarly, for the approximate posterior , we use a special Gaussian distribution with parameters given by an encoder MLP with parameters :
This makes probabilistic encoding and decoding simple: we simply map our data to the mean and variance parameters of a Gaussian distribution for encoding, and vice versa for decoding. For learning the encoder and decoder, we start from the maximum likelihood objective Section 5.1.4, and derive a convenient lower bound known as the evidence lower bound, or ELBO. Starting from simple algebraic manipulations
we take expectations with respect to and use the Gibbs inequality (Theorem 3.1) to get
The right-hand side of this bound is the ELBO; as a lower bound for the pointwise log-likelihood of , its maximization offers a principled compromise between the maximum likelihood objective and computational tractability. Interestingly, the derivation above shows that its tightness depends on the KL divergence between the approximate posterior and the true posterior , implying that the more accurate our approximate posterior is, the more maximization of the ELBO leads to maximization of the underlying objective of interest, the likelihood of the data. Thus, the VAE objective is:
| (5.1.14) |
By our derivation, maximization of this objective corresponds to a tradeoff between maximizing the likelihood function of the data and minimizing the KL divergence between the approximate and true posterior, which is a highly sensible objective given the VAE modeling assumptions.
VAE Training as Probabilistic Autoencoding
There is a general methodology for maximizing the ELBO objective in Equation 5.1.14 using stochastic gradient descent and various tractable Monte Carlo estimators for the associated gradients. However, the task is simpler under the Gaussian assumptions we have made above. In this case, the ELBO reads
| (5.1.15) |
following Theorem B.1 and the Gaussian entropy calculation done in Appendix B, where denotes equivalence of optimization objectives (in each case, we remove some additive constants that do not change the optimization problem’s solutions). The remaining term corresponds to the “autoencoding” part of the ELBO objective: intuitively, it seeks to maximize the likelihood of data generated by the decoder when the latents are distribited according to the approximate posterior (generated by the encoder applied to a data sample ), which is a probabilistic form of autoencoding. To see this more directly, consider the special case where the approximate posterior concentrates on its mean , for every : this is the limit where its log-variance for each coordinate . For simplicity, assume moreover that , giving the decoder constant unit variance on each coordinate. Then the loss term in question converges to
So with a highly confident encoder, which deterministically maps each sample to a single point in -space, and an isotropic decoder, the “autoencoding” part of the ELBO maximization problem indeed becomes a classical autoencoding objective!555In the general case where is not fixed as , the reader can verify that the autoencoding term in the ELBO objective converges to a regularized classical autoencoding objective. At the same time, note that this special case is actually excluded by the extra terms in Equation 5.1.15—these effectively correspond to regularization terms that discourage the encoder from collapsing. The general ELBO loss (Equations 5.1.14 and 5.1.15) is therefore a strict generalization of the classical autoencoding reconstruction objective (Equation 5.1.12), both in terms of its data fidelity term and in terms of the inclusion of regularization terms.
Training a VAE
VAEs are typically trained by alternating stochastic gradient ascent on the ELBO objective (Equation 5.1.15), given individual samples from the true data distribution and from . In particular, it is standard to collect and train on many independently-generated samples for each sample . To take gradients of Equation 5.1.15 with respect to the encoder parameters , one makes use of the so-called reparameterization trick by writing as
where denotes equality in distribution. Then one can simply take many independent standard Gaussian samples for each data sample , generate the corresponding samples from the approximate posterior , and compute gradients with respect to using automatic differentiation without any issues.
5.2 Learning Self-Consistent Representations
In earlier chapters, we have studied methods that would allow us to learn a low-dimensional distribution via (lossy) compression. As we have mentioned in Chapter 1 and demonstrated in the previous chapters, the progresses made in machine intelligence largely rely on finding computationally feasible and efficient solutions to realize the desired compression, not only computable or tractable in theory, but also scalable in practice:
| (5.2.1) |
It is even fair to say that the tremendous advancement in machine intelligence made in the past decade or so is largely attributed to the development of scalable models and methods, say by training deep networks via back propagation. Large models with billions of parameters trained with trillions of data points on tens of thousands of powerful GPUs have demonstrated super-human capabilities in memorizing existing knowledge. This has led many to believe that the “intelligence” of such models will continue to improve as their scale continues to go up.
While we celebrate the engineering marvels of such large man-made machine learning systems, we also must admit that, compared to intelligence in nature, this approach to improving machine intelligence is unnecessarily resource-demanding. Natural intelligent beings, including animals and humans, simply cannot afford such a brute-force solution for learning because they must operate with a very limited budget in energy, space, and time, subject to many strict physical constraints.
First, there is strong scientific evidence that our brain does not conduct global end-to-end back propagation to improve or correct its predictions. Instead, it has long been known in neuroscience that our brain corrects errors with local closed-loop feedback, such as predictive coding. This was the scientific basis that inspired Norbert Wiener to develop the theory of feedback control and the Cybernetics program back in the 1940s.
Second, we saw in the previous sections that in order to learn a consistent representation, one needs to learn a bidirectional autoencoding:
| (5.2.2) |
It requires enforcing the observed input data and the decoded to be close by some measure of similarity . In nature, animals or humans rarely have direct access to the ground truth . For example, we never have direct access to true 3D shape, distance, or dynamics of objects in a scene. Yet, we have all learned to estimate and predict them very accurately and efficiently. Hence, an outstanding question is: how can we learn the true distribution of , even though we cannot directly compare our estimate with the ground truth ? As we will see in this chapter, the answer also lies in the closed-loop feedback, as well as the low-dimensionality of the data distribution.
As we know from the previous chapter, in order to ensure that a representation is consistent, we need to compare the generated and the original , at least in distribution. Even when we do have access to and , technically, computing and minimizing the distance between two distributions can be problematic, especially when the support of the distributions is low-dimensional. The KL-divergence introduced in Chapter 3 is not even well-defined between two distributions that do not have overlapping supports.
As an early attempt to alleviate the above difficulty in computing and minimizing the distance between two (low-dimensional) distributions, people had suggested learning the generator/decoder via discriminative approaches [Tu07]. This line of thought has led to the idea of Generative Adversarial Nets (GAN) [GPM+14a]. It introduces a discriminator , usually modeled by a deep network, to discern differences between the generated samples and the real ones :
| (5.2.3) |
It is suggested that we may attempt to align the distributions between and via a Stackelberg game between the generator and the discriminator :
| (5.2.4) |
That is, the discriminator is trying to minimize the cross entropy between the true samples and the generated ones while the generator is trying to do the opposite.
One may show that finding an equilibrium for the above Stackelberg game is equivalent to minimizing the Jensen-Shannon divergence:
| (5.2.5) |
Note that, compared to the KL-divergence, the JS-divergence is well-defined even if the supports of the two distributions are non-overlapping. However, JS-divergence does not have a closed-form expression even between two Gaussians, whereas KL-divergence does. In addition, since the data distributions are low-dimensional, the JS-divergence can be highly ill-conditioned to optimize.666as shown in [ACB17]. This may explain why many additional heuristics are typically used in many subsequent variants of GAN.
So, instead, it has also been suggested to replace JS-divergence with the earth mover (EM) distance or the Wasserstein distance.777Roughly speaking, for distributions with potentially non-overlapping low-dimensional supports, the JS-divergence behaves like the -norm, and the EM-distance behaves like the -norm. However, both the JS-divergence and Wasserstein distance can only be approximately computed between two general distributions.888For instance, the Wasserstein distance requires one to compute the maximal difference between expectations of the two distributions over all 1-Lipschitz functions. Furthermore, neither the JS-divergence nor the Wasserstein distance has closed-form formulae, even for Gaussian distributions.999The (-norm) Wasserstein distance can be bounded by the (-norm) Wasserstein distance which has a closed-form [DDS22]. However, as is well-known in high-dimensional geometry, -norm and norm deviate significantly in terms of their geometric and statistical properties as the dimension becomes high [WM21]. The bound can become very loose.
If it is difficult to compare distributions of the data and , would it be possible to compare the learned feature with its image under the encoder :
| (5.2.6) |
This leads to the notion of self-consistent representation.
Definition 5.2 (Self-Consistent Representation).
Given data , we call a self-consistent representation a pair of functions , such that the features are compact and structured, and the autoencoding features are close to .
-
1.
We say that it is sample-wise self-consistent if in a certain norm with high probability.
-
2.
We say that the representation is distributionally self-consistent if .
5.2.1 Closed-Loop Transcription via Stackelberg Games
How do we try to ensure a learned representation is self-consistent? As usual, let us assume with each subset of samples belonging to a low-dimensional submanifold: . Following the notation in Chapter 3, we use a matrix to denote the membership of sample belonging to class and otherwise. One seeks a continuous mapping from to an optimal representation :
| (5.2.7) |
which maximizes the following coding rate-reduction (MCR2) objective:
| (5.2.8) |
where , , for each .
One issue with learning such a one-sided mapping (5.2.7) via maximizing the above objective (5.2.8) is that it tends to expand the dimension of the learned subspace for features in each class101010If the dimension of the feature space is too high, maximizing the rate reduction may over-estimate the dimension of each class. Hence, to learn a good representation, one needs to pre-select a proper dimension for the feature space, as achieved in the experiments in [YCY+20]. In fact the same “model selection” problem persists even in the simplest single-subspace case, which is the classic PCA [Jol86]. To our best knowledge, selecting the correct number of principal components in a heterogeneous noisy situation remains an active research topic [HSD20]., as we have seen in Section 3.4 of Chapter 3. To verify whether the learned features are consistent, meaning neither over-estimating nor under-estimating the intrinsic data structure, we may consider learning a decoder from the representation back to the data space : :
| (5.2.9) |
and check how close and are. This forms an autoencoding which is what we have studied extensively in the previous Chapter 5.
Measuring distance in the feature space.
However, as we have discussed above, if we do not have the option to compute the distance between and , we are left with the option of comparing their corresponding features and . Notice that under the MCR2 objective, the distributions of the resulting or tend to be piecewise linear so their distance can be computed more easily. More precisely, since the features of each class, and , are close to being a low-dimensional subspace/Gaussian, their “distance” can be measured by the rate reduction, with (5.2.8) restricted to two sets of equal size:
| (5.2.10) |
The overall distance between and is given by:
| (5.2.11) |
If we are interested in discerning any differences in the distributions of the original data and their decoded , we may view the feature encoder as a “discriminator” to magnify any difference between all pairs of and , by simply maximizing the distance :
| (5.2.12) |
That is, a “distance” between and can be measured as the maximally achievable rate reduction between all pairs of classes in these two sets. In a way, this measures how well or badly the decoded aligns with the original data —hence measuring the goodness of “injectivity” of the encoder . Notice that such a discriminative measure is consistent with the idea of GAN (5.2.3) that tries to separate and into two classes, measured by the cross-entropy.
Nevertheless, here the discriminative encoder naturally generalizes to cases when the data distributions are multi-class and multi-modal, and the discriminativeness is measured with a more refined measure—the rate reduction—instead of the typical two-class loss (e.g., cross entropy) used in GANs. That is, we may view the encoder as a generalized discriminator that replaces the binary classifier in (5.2.3):
| (5.2.13) |
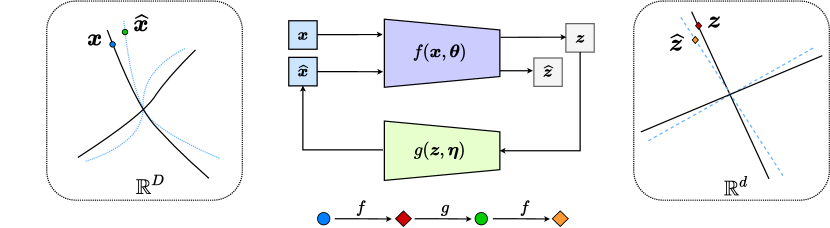
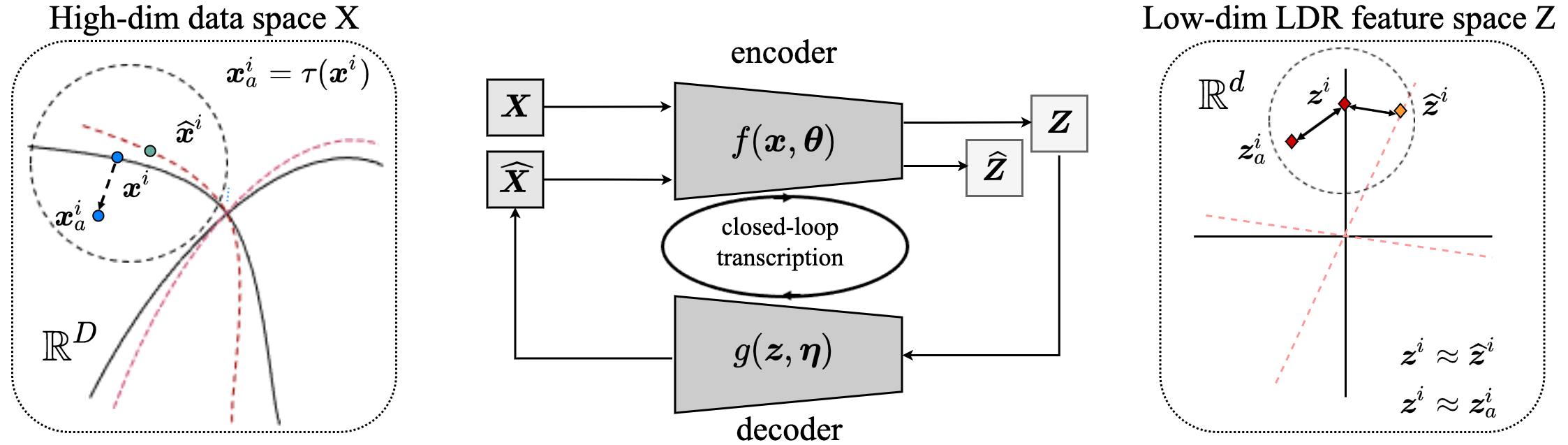
The overall pipeline can be illustrated by the following “closed-loop” diagram:
| (5.2.14) |
where the overall model has parameters: . Figure 5.6 shows the overall process.
Encoder and decoder as a two-player game.
Obviously, to ensure the learned autoencoding is self-consistent, the main goal of the decoder is to minimize the distance between and . That is, to learn , we want to minimize the distance :
| (5.2.15) |
where and .
Example 5.2.
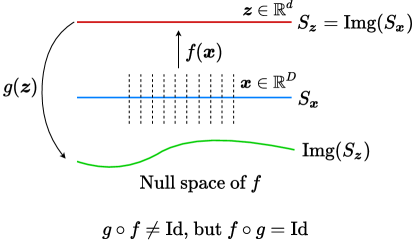
One may wonder why we need the mapping to function as a discriminator between and by maximizing . Figure 5.7 gives a simple illustration: there might be many decoders such that is an identity (Id) mapping. for all in the subspace in the feature space. However, is not necessarily an autoencoding map for in the original distribution (here drawn as a subspace for simplicity). That is, , let alone or . One should expect that, without careful control of the image of , this would be the case with high probability, especially when the support of the distribution of is extremely low-dimensional in the original high-dimensional data space.
Comparing the contractive and contrastive nature of (5.2.15) and (5.2.12) on the same distance measure, we see the roles of the encoder and the decoder naturally as “a two-player game”: while the encoder tries to magnify the difference between the original data and their transcribed data, the decoder aims to minimize the difference. Now for convenience, let us define the “closed-loop encoding” function:
| (5.2.16) |
Ideally, we want this function to be very close to or at least the distributions of their images should be close. With this notation, combining (5.2.15) and (5.2.12), a closed-loop notion of “distance” between and can be computed as an equilibrium point to the following Stackelberg game (cf Section A.3) for the same utility in terms of rate reduction:
| (5.2.17) |
Notice that this only measures the difference between (features of) the original data and its transcribed version. It does not measure how good the representation (or ) is for the multiple classes within (or ). To this end, we may combine the above distance with the original MCR2-type objectives (5.2.8): namely, the rate reduction and for the learned LDR for and for the decoded . Notice that although the encoder tries to maximize the multi-class rate reduction of the features of the data , the decoder should minimize the rate reduction of the multi-class features of the decoded . That is, the decoder tries to use a minimal coding rate needed to achieve a good decoding quality.
Hence, the overall “multi-class” Stackelberg game for learning the closed-loop transcription, named CTRL-Multi, is
| (5.2.18) | |||||
| (5.2.19) | |||||
| (5.2.20) |
subject to certain constraints (upper or lower bounds) on the first term and the second term.
Notice that, without the terms associated with the generative part or with all such terms fixed as constant, the above objective is precisely the original MCR2 objective introduced in Chapter 3. In an unsupervised setting, if we view each sample (and its augmentations) as its own class, the above formulation remains exactly the same. The number of classes is simply the number of independent samples. In addition, notice that the above game’s objective function depends only on (features of) the data , hence one can learn the encoder and decoder (parameters) without the need for sampling or matching any additional distribution (as typically needed in GANs or VAEs).
As a special case, if only has one class, the Stackelberg game reduces to a special “two-class” or “binary” form,111111As the first two rate reduction terms automatically become zero named CTRL-Binary,
| (5.2.21) |
between and the decoded by viewing and as two classes . Notice that this binary case resembles the formulation of the original GAN (5.2.3). Instead of using cross entropy, our formulation adopts a more refined rate-reduction measure, which has been shown to promote diversity in the learned representation in Chapter 3.
Sometimes, even when contains multiple classes/modes, one could still view all classes together as one class. Then, the above binary objective is to align the union distribution of all classes with their decoded . This is typically a simpler task to achieve than the multi-class one (5.2.20), since it does not require learning of a more refined multi-class CTRL for the data, as we will later see in experiments. Notice that one good characteristic of the above formulation is that all quantities in the objectives are measured in terms of rate reduction for the learned features (assuming features eventually become subspace Gaussians).
One may notice that the above learning framework draws inspiration from closed-loop error correction widely practiced in feedback control systems. The closed-loop mechanism is used to form an overall feedback system between the two encoding and decoding networks for correcting any “error” in the distributions between the data and the decoded . Using terminology from control theory, one may view the encoding network as a “sensor” for error feedback while the decoding network as a “controller” for error correction. However, notice that here the “target” for control is not a scalar nor a finite dimensional vector, but a continuous distribution—in order for the distribution of to match that of the data . This is in general a control problem in an infinite dimensional space. The space of possible diffeomorphisms of submanifolds that tries to model is infinite-dimensional [Lee02]. Ideally, we hope when the sensor and the controller are optimal, the distribution of becomes a “fixed point” for the closed loop while the distribution of reaches a compact linear discriminative representation. Hence, the minimax programs (5.2.20) and (5.2.21) can also be interpreted as games between an error-feedback sensor and an error-reducing controller.
The remaining question is whether the above framework can indeed learn a good (autoencoding) representation of a given dataset? Before we give some formal theoretical justification (in the next subsection), we present some empirical results.
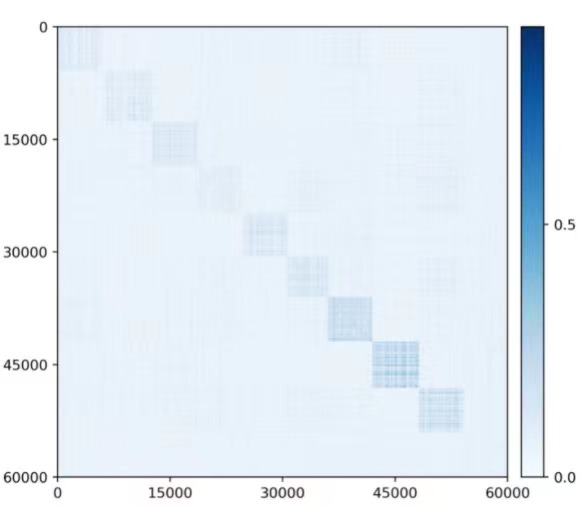
Visualizing correlation of features and decoded features .
We visualize the cosine similarity between and learned from the multi-class objective (5.2.20) on MNIST, CIFAR-10 and ImageNet (10 classes), which indicates how close is from . Results in Figure 5.8 show that and are aligned very well within each class. The block-diagonal patterns for MNIST are sharper than those for CIFAR-10 and ImageNet, as images in CIFAR-10 and ImageNet have more diverse visual appearances.
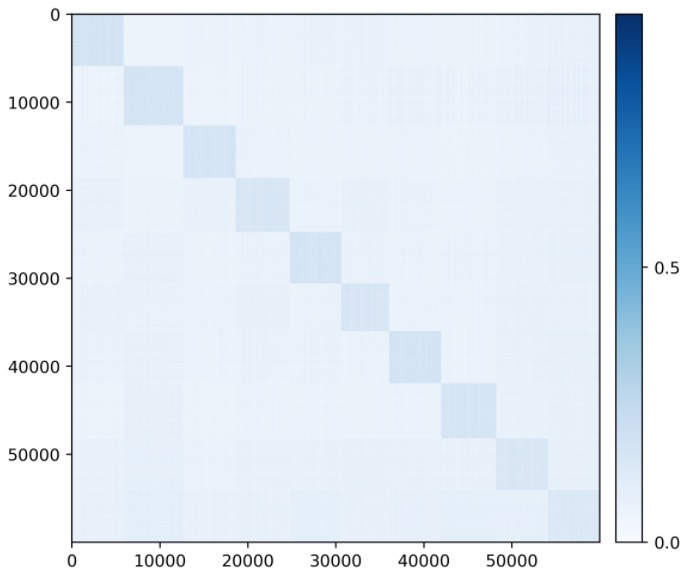
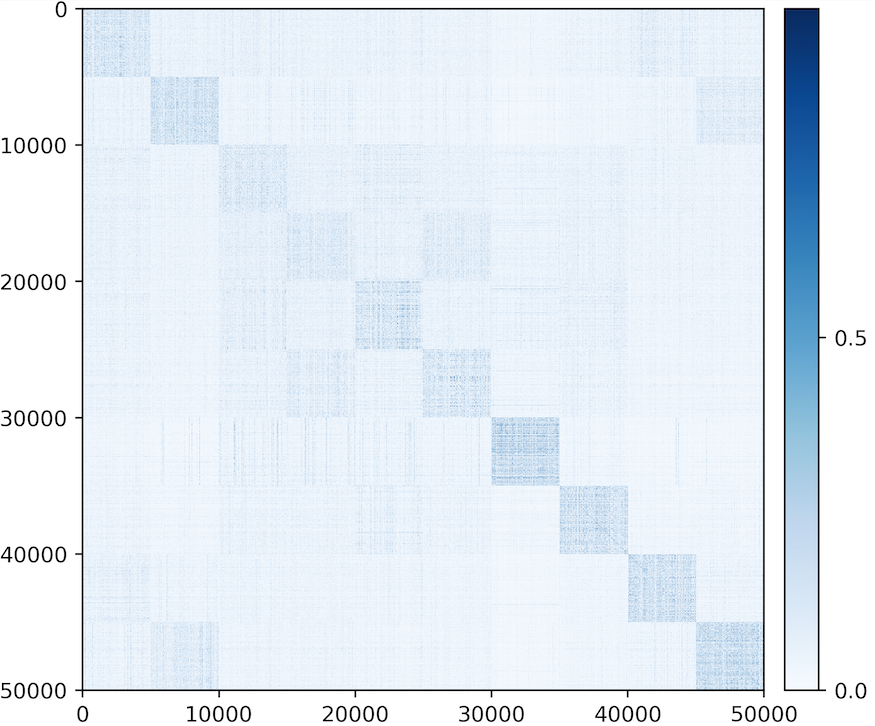
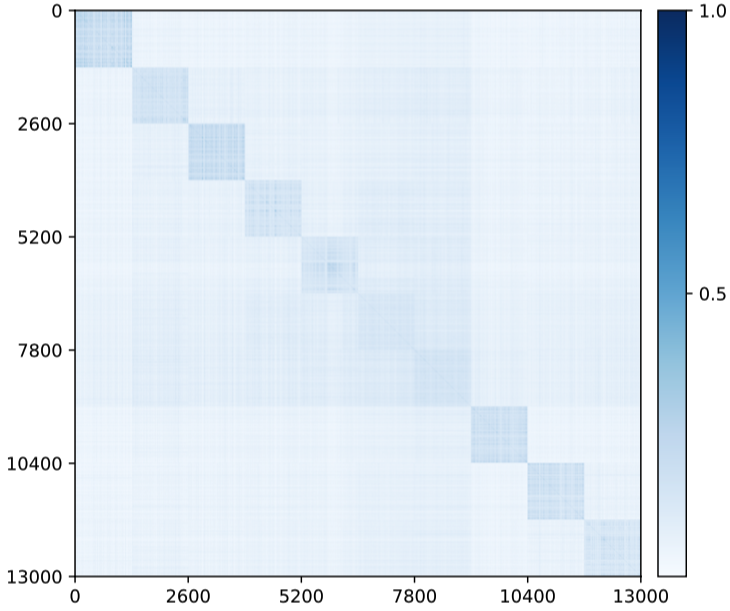
Visualizing autoencoding of the data and the decoded .
We compare some representative and on MNIST, CIFAR-10 and ImageNet (10 classes) to verify how close is to . The results are shown in Figure 5.9, and visualizations are created from training samples. Visually, the autoencoded faithfully captures major visual features from its respective training sample , especially the pose, shape, and layout. For the simpler dataset such as MNIST, autoencoded images are almost identical to the original.






5.2.2 A Mixture of Low-Dimensional Gaussians
In the above, we have argued that it is possible to formulate the problem of learning a data distribution as a closed-loop autoencoding problem. We also saw empirically that such a scheme seems to work. The remaining question is when and why such a scheme should work. It is difficult to answer this question for the most general cases with arbitrary data distributions. Nevertheless, as usual, let us see if we can arrive at a rigorous justification for the ideal case when the data distribution is a mixture of low-dimensional subspaces or low-rank Gaussians. A clear characterization and understanding of this important special case would shed light on the more general cases.121212As most distributions with low-dimensional structures can be well-approximated by this family of distributions.
To this end, let us first suppose that is distributed according to a mixture of low-dimensional Gaussians, and the label (i.e., subspace assignment) for is given by . Then, let us set up a minimax optimization problem to learn the data distribution, say through learning an encoding of into representations which are supported on a mixture of orthogonal subspaces, and a decoding of back into . Then, the representation we want to achieve is maximized by the earlier-discussed version of the information gain, i.e., , which enforces that the representation of each class spans a subspace which is orthogonal to the supporting subspaces of other classes. The way to measure the consistency of the decoding is, as before, given by , which enforces that the representation and its autoencoding for each class span the same subspace. Thus, we can set up a simplified Stackelberg game:
| (5.2.22) |
Notice that this is a simpler setup than what is used in practice—there is no term, for instance, and we work in the supervised setting with class labels (although the techniques used to prove the following result are easy to extend to unsupervised formulations). Also, the consistency of the representations is only measured in a distribution-wise sense via (though this may be substituted with a sample-wise distance metric such as the norm if desired, and equivalent conclusions may be drawn, mutatis mutandis).
Under mild conditions, in order to realize the desired encoder and decoder which realize from a data source that is already distributed according to a mixture of correlated low-dimensional Gaussians, we only require a linear encoder and decoder to disentangle and whiten the Gaussians. We then study this setting in the case where and parameterize matrices whose operator norm is constrained.
We want to understand what kinds of optima are learned in this setting. One suitable solution concept for this kind of game, where the decoder’s optimal solution is defined solely with respect to the encoder (and not, in particular, with respect to some other intrinsic property of the decoder), is a Stackelberg equilibrium where the decoder follows the encoder. Namely, at such an equilibrium, the decoder should optimize its objective; meanwhile the encoder should optimize its objective, given that whatever it picks, the decoder will pick an optimal response (which may affect the encoder objective). In game-theoretic terms, it is like the decoder goes second: it chooses its weights after the encoder, and both the encoder and decoder attempt to optimize their objective in light of this. It is computationally tractable to learn sequential equilibria via gradient methods via alternating optimization, where each side uses different learning rates. Detailed exposition of sequential equilibria is beyond the scope of this book and we provide more technical details in Section A.3. In this setting, we have the following result:
Theorem 5.1 ([PPC+23], Abridged).
Suppose that is distributed on a mixture of subspaces. Under certain realistic yet technical conditions, it holds that all sequential equilibria of (5.2.22) obey:
-
•
The lie on orthogonal subspaces and are isotropic on those subspaces, i.e., maximizing the information gain.
-
•
The autoencoding is self-consistent, i.e., the subspaces spanned by and are the same for all .
This notion of self-consistency is the most one can expect if there are only geometric assumptions on the data, i.e., there are no statistical assumptions. If we assume that the columns of is drawn from a low-rank Gaussian mixture model, then analogous versions of this theorem certify that are also low-rank Gaussians whose covariance is isotropic, for instance. Essentially, this result validates, via the simple case of Gaussian mixtures on subspaces, that minimax games to optimize the information gain and self-consistency may achieve optimal solutions.
5.3 Continuous Learning Self-Consistent Representations
5.3.1 Class-wise Incremental Learning
As we have seen, deep neural networks have demonstrated a great ability to learn representations for hundreds or even thousands of classes of objects, in both discriminative and generative contexts. However, networks typically must be trained offline, with uniformly sampled data from all classes simultaneously. It has been known that when an (open-loop) network is updated to learn new classes without data from the old ones, previously learned knowledge will fall victim to the problem of catastrophic forgetting [MC89]. This is known in neuroscience as the stability-plasticity dilemma: the challenge of ensuring that a neural system can learn from a new environment while retaining essential knowledge from previous ones [Gro87].
In contrast, natural neural systems (e.g., animal brains) do not seem to suffer from such catastrophic forgetting at all. They are capable of developing new memory of new objects while retaining memory of previously learned objects. This ability, for either natural or artificial neural systems, is often referred to as incremental learning, continual learning, sequential learning, or lifelong learning [AR20].
While many recent works have highlighted how artificial neural systems can be trained in more flexible ways, the strongest existing efforts toward answering the stability-plasticity dilemma for artificial neural networks typically require either storing raw exemplars [RKS+17, CRE+19] or providing external mechanisms [KPR+17]. Raw exemplars, particularly in the case of high-dimensional inputs like images, are costly and difficult to scale, while external mechanisms—which typically include secondary networks and representation spaces for generative replay, incremental allocation of network resources, network duplication, or explicit isolation of used and unused parts of the network—require heuristics and incur hidden costs.
Here we are interested in an incremental learning setting that is similar to nature. It counters these existing practices with two key qualities.
-
1.
The first is that it should be memory-based. When learning new classes, no raw exemplars of old classes are available to train the network together with new data. This implies that one has to rely on a compact and thus structured “memory” learned for old classes, such as incrementally learned generative representations of the old classes, as well as the associated encoding and decoding mappings [KK18].
-
2.
The second is that it should be self-contained. Incremental learning takes place in a single neural system with a fixed capacity, and in a common representation space. The ability to minimize forgetting is implied by optimizing an overall learning objective, without external networks, architectural modifications, or resource allocation mechanisms.
The incoherent linear structures for features of different classes closely resemble how objects are encoded in different areas of the inferotemporal cortex of animal brains [CT17, BSM+20]. The closed-loop transcription also resembles popularly hypothesized mechanisms for memory formation [VST+20, JT20]. This leads to a question: since memory in the brain is formed in an incremental fashion, can the above closed-loop transcription framework also support incremental learning?
LDR memory sampling and replay.
The simple linear structures of LDR make it uniquely suited for incremental learning: the distribution of features of each previously learned class can be explicitly and concisely represented by a principal subspace in the feature space. To preserve the memory of an old class , we only need to preserve the subspace while learning new classes. To this end, we simply sample representative prototype features on the subspace along its top principal components, and denote these features as . Because of the simple linear structures of LDR, we can sample from by calculating the mean and covariance of after learning class . The storage required is extremely small, since we only need to store means and covariances, which are sampled from as needed. Suppose a total of old classes have been learned so far. If prototype features, denoted , for all of these classes can be preserved when learning new classes, the subspaces representing past memory will be preserved as well. Details about sampling and calculating mean and covariance can be found in the work of [TDW+23].
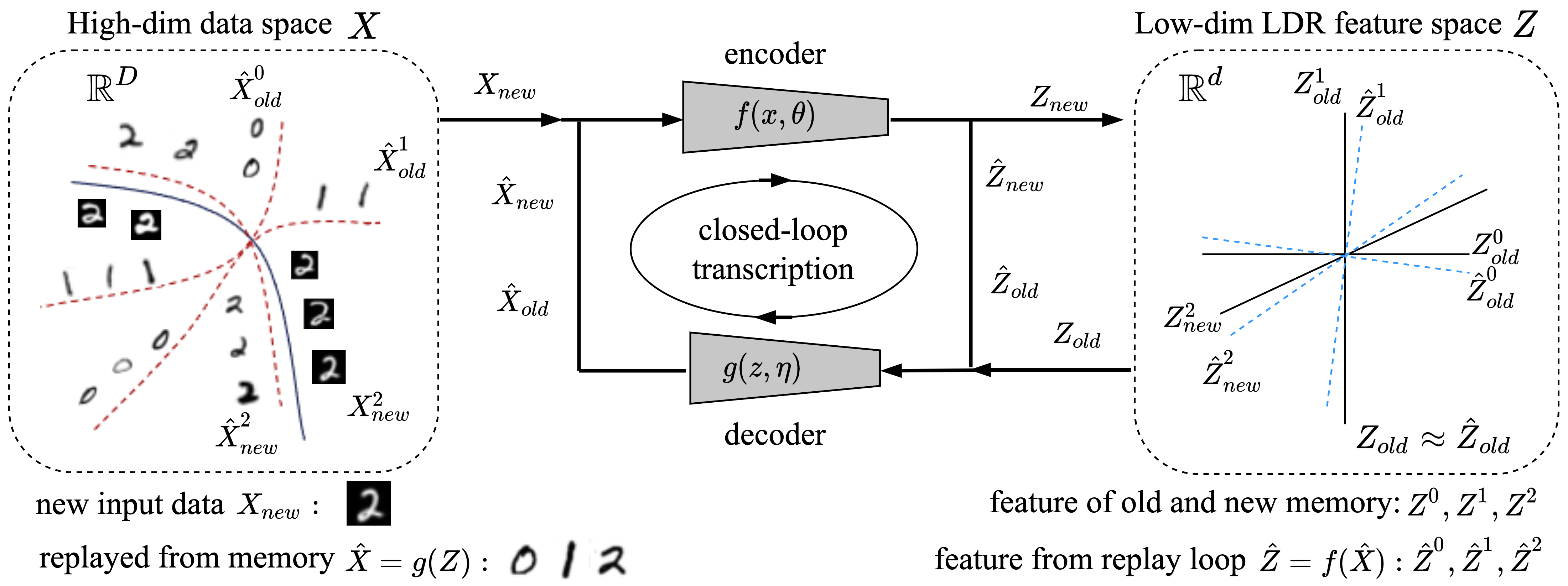
Incremental learning LDR with an old-memory constraint.
Notice that, with the learned autoencoding (5.2.9), one can replay and use the images, say , associated with the memory features to avoid forgetting while learning new classes. This is typically how generative models have been used for prior incremental learning methods. However, with the closed-loop framework, explicitly replaying images from the features is not necessary. Past memory can be effectively preserved through optimization exclusively on the features themselves.
Consider the task of incrementally learning a new class of objects.131313Of course, one may also consider the more general setting where the task contains a small batch of new classes, without serious modification. We denote a corresponding new sample set as . The features of are denoted as . We concatenate them together with the prototype features of the old classes and form . We denote the replayed images from all features as although we do not actually need to compute or use them explicitly. We only need features of replayed images, denoted .
Mirroring the motivation for the multi-class CTRL objective (5.2.20), we would like the features of the new class to be incoherent to all of the old ones . As is the only new class whose features need to be learned, the objective (5.2.20) reduces to the case where :
| (5.3.1) |
However, when we update the network parameters to optimize the features for the new class, the updated mappings and will change features of the old classes too. Hence, to minimize the distortion of the old class representations, we can try to enforce . In other words, while learning new classes, we enforce that the memory of old classes remains “self-consistent” through the transcription loop:
| (5.3.2) |
Mathematically, this is equivalent to setting
Hence, the above minimax program (5.3.1) is revised as a constrained minimax game, which we refer to as incremental closed-loop transcription (i-CTRL). The objective of this game is identical to the standard multi-class CTRL objective (5.2.20), but includes just one additional constraint:
| (5.3.3) | |||||
In practice, the constrained minimax program can be solved by alternating minimization and maximization between the encoder and decoder as follows:
| (5.3.4) | |||||
| (5.3.5) |
where the constraint in (5.3.3) has been converted (and relaxed) to a Lagrangian term with a corresponding coefficient and sign. We additionally introduce another coefficient for weighting the rate reduction term associated with the new data.
Jointly optimal memory via incremental reviewing.
As we will see, the above constrained minimax program can already achieve state-of-the-art performance for incremental learning. Nevertheless, developing an optimal memory for all classes cannot rely on graceful forgetting alone. Even for humans, if an object class is learned only once, we should expect the learned memory to fade as we continue to learn new ones, unless the memory can be consolidated by reviewing old object classes.
To emulate this phase of memory forming, after incrementally learning a whole dataset, we may go back to review all classes again, one class at a time. We refer to going through all classes once as one reviewing “cycle”.141414to distinguish from the term “epoch” used in the conventional joint learning setting. If needed, multiple reviewing cycles can be conducted. It is quite expected that reviewing can improve the learned (LDR) memory. But somewhat surprisingly, the closed-loop framework allows us to review even in a “class-unsupervised” manner: when reviewing data of an old class, say , the system does not need the class label and can simply treat as a new class . That is, the system optimizes the same constrained mini-max program (5.3.3) without any modification; after the system is optimized, one can identify the newly learned subspace spanned by , and use it to replace or merge with the old subspace . As our experiments show, such a class-unsupervised incremental review process can gradually improve both discriminative and generative performance of the LDR memory, eventually converging to that of a jointly learned memory.
Experimental verification.
We show some experimental results on the following datasets: MNIST [LBB+98a] and CIFAR-10 [KNH14]. All experiments are conducted for the more challenging class-IL setting. For both MNIST and CIFAR-10, the 10 classes are split into 5 tasks with 2 classes each or 10 tasks with 1 class each. For the encoder and decoder , we adopt a very simple network architecture modified from DCGAN [RMC16], which is merely a four-layer convolutional network. Here we only show some qualitative visual results; more experiments and analytical analysis can be found in the work [TDW+23].
Visualizing auto-encoding properties.
We begin by qualitatively visualizing some representative images and the corresponding replayed on MNIST and CIFAR-10. The model is learned incrementally with the datasets split into 5 tasks. Results are shown in Figure 5.11, where we observe that the reconstructed preserves the main visual characteristics of including shapes and textures. For a simpler dataset like MNIST, the replayed are almost identical to the input ! This is rather remarkable given: (1) our method does not explicitly enforce for individual samples as most autoencoding methods do, and (2) after having incrementally learned all classes, the generator has not forgotten how to generate digits learned earlier, such as 0, 1, 2. For a more complex dataset like CIFAR-10, we also demonstrate good visual quality, faithfully capturing the essence of each image.




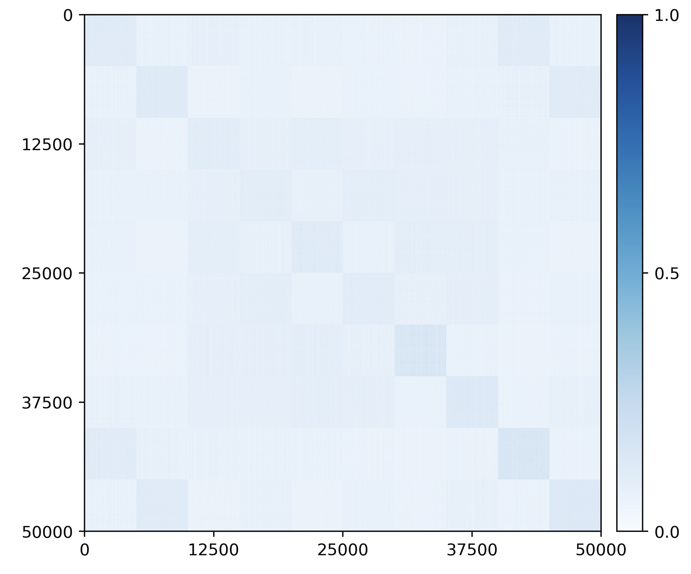
Principal subspaces of the learned features.
Most generative memory-based methods utilize autoencoders, VAEs, or GANs for replay purposes. The structure or distribution of the learned features for each class is unclear in the feature space. The features of the LDR memory, on the other hand, have a clear linear structure. Figure 5.12 visualizes correlations among all learned features , in which we observe clear block-diagonal patterns for both datasets.151515Notice that these patterns closely resemble the similarity matrix of response profiles of object categories from different areas of the inferotemporal cortex, as shown in Extended DataFig.3 of [BSM+20]. This indicates that the features for different classes indeed lie on subspaces that are incoherent from one another. Hence, features of each class can be well modeled as a principal subspace in the feature space.
Replay images of samples from principal components.
Since features of each class can be modeled as a principal subspace, we further visualize the individual principal components within each of those subspaces. Figure 5.13 shows the images replayed from sampled features along the top-4 principal components for different classes, on MNIST and CIFAR-10 respectively. Each row represents samples along one principal component, and they clearly show similar visual characteristics but are distinctively different from those in other rows. We see that the model remembers different poses of ‘4’ after having learned all remaining classes. For CIFAR-10, the incrementally learned memory remembers representative poses and shapes of horses and ships.




Effectiveness of incremental reviewing.
We verify how the incrementally learned LDR memory can be further consolidated with an unsupervised incremental reviewing phase described before. Experiments are conducted on CIFAR-10, with 10 steps. Figure 5.14 left shows replayed images of the first class ‘airplane’ at the end of incremental learning of all ten classes, sampled along the top-3 principal components – every two rows (16 images) are along one principal direction. Their visual quality remains very decent—we observe almost no forgetting. The right figure shows replayed images after reviewing the first class once. We notice a significant improvement in visual quality after reviewing, and principal components of the features in the subspace start to correspond to distinctively different visual attributes within the same class.


5.3.2 Sample-wise Continuous Unsupervised Learning
As we know, the closed-loop CTRL formulation can already learn a decent autoencoding, even without class information, with the CTRL-Binary program:
| (5.3.6) |
However, note that (5.3.6) is practically limited because it only aligns the dataset and the regenerated at the distribution level. There is no guarantee that each sample would be close to the decoded .
Sample-wise constraints for unsupervised transcription.
To improve discriminative and generative properties of representations learned in the unsupervised setting, we propose two additional mechanisms for the above CTRL-Binary maximin game (5.3.6). For simplicity and uniformity, here these will be formulated as equality constraints over rate reduction measures, but in practice they can be enforced softly during optimization.
Sample-wise self-consistency via closed-loop transcription.
First, to address the issue that CTRL-Binary does not learn a sample-wise consistent autoencoding, we need to promote to be close to for each sample. In the CTRL framework, this can be achieved by enforcing their corresponding features and to be close. To promote sample-wise self-consistency, where is close to , we want the distance between and to be zero or small, for all samples. This distance can be measured by the rate reduction:
| (5.3.7) |
Note that this again avoids measuring differences in the image space.
Self-supervision via compressing augmented samples.
Since we do not know any class label information between samples in the unsupervised setting, the best we can do is to view every sample and its augmentations (say via translation, rotation, occlusion, etc.) as one “class”—a basic idea behind almost all self-supervised learning methods. In the rate reduction framework, it is natural to compress the features of each sample and its augmentations. In this work, we adopt the standard transformations in SimCLR [CKN+20] and denote such a transformation as . We denote each augmented sample , and its corresponding feature as . For discriminative purposes, we hope the classifier is invariant to such transformations. Hence it is natural to enforce that the features of all augmentations are the same as those of the original sample . This is equivalent to requiring the distance between and , measured in terms of rate reduction again, to be zero (or small) for all samples:
| (5.3.8) |
Unsupervised representation learning via closed-loop transcription.
So far, we know the CTRL-Binary objective in (5.3.6) helps align the distributions while sample-wise self-consistency (5.3.7) and sample-wise augmentation (5.3.8) help align and compress features associated with each sample. Besides consistency, we also want learned representations to be maximally discriminative for different samples (here viewed as different “classes”). Notice that the rate distortion term measures the coding rate (hence volume) of all features.
Unsupervised CTRL.
Putting these elements together, we propose to learn a representation via the following constrained maximin program, which we refer to as unsupervised CTRL (u-CTRL):
| (5.3.9) | ||||
| subject to |
Figure 5.15 illustrates the overall architecture of the closed-loop system associated with this program.
In practice, the above program can be optimized by alternating maximization and minimization between the encoder and the decoder . We adopt the following optimization strategy that works well in practice, which is used for all subsequent experiments on real image datasets:
| (5.3.10) | |||
| (5.3.11) |
where the constraints and in (5.3.9) have been converted (and relaxed) to Lagrangian terms with corresponding coefficients and .161616Notice that computing the rate reduction terms for all samples or a batch of samples requires computing the expensive of large matrices. In practice, from the geometric meaning of for two vectors, can be approximated with an norm or the cosine distance between two vectors.
The above representation is learned without class information. In order to facilitate discriminative or generative tasks, it must be highly structured. It has been verified experimentally that this is indeed the case and u-CTRL demonstrates significant advantages over other incremental or unsupervised learning methods [TDC+24]. We here only illustrate some qualitative results with the experiment on the CIFAR-10 dataset [KNH14], with standard augmentations for self-supervised learning [CKN+20]. One may refer to [TDC+24] for experiments on more and larger datasets and their quantitative evaluations.
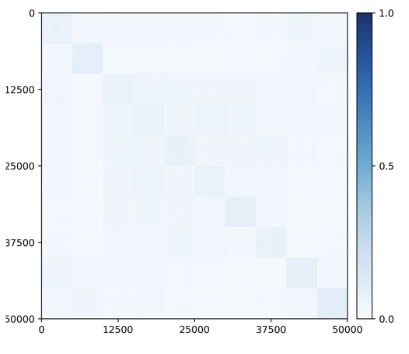
As one can see from the experiments, specific and unique structure indeed emerges naturally in the representations learned using u-CTRL: globally, features of images in the same class tend to be clustered well together and separated from other classes, as shown in Figure 5.16; locally, features around individual samples exhibit approximately piecewise linear low-dimensional structures, as shown in Figure 5.17.


Unsupervised conditional image generation via rate reduction.
The highly-structured feature distribution also suggests that the learned representation can be very useful for generative purposes. For example, we can organize the sample features into meaningful clusters, and model them with low-dimensional (Gaussian) distributions or subspaces. By sampling from these compact models, we can conditionally regenerate meaningful samples from computed clusters. This is known as unsupervised conditional image generation [HKJ+21].
To cluster features, we exploit the fact that the rate reduction framework (3.4.12) is inspired by unsupervised clustering via compression [MDH+07a], which provides a principled way to find the membership . Concretely, we maximize the same rate reduction objective (3.4.12) over , but fix the learned representation instead. We simply view the membership as a nonlinear function of the features , say with parameters . In practice, we model this function with a simple neural network, such as an MLP head right after the output feature . To estimate a “pseudo” membership of the samples, we solve the following optimization problem over :
| (5.3.12) |
In Figure 5.18, we visualize images generated from the ten unsupervised clusters from (5.3.12). Each block represents one cluster and each row represents one principal component for each cluster. Despite learning and training without labels, the model not only organizes samples into correct clusters, but is also able to preserve statistical diversities within each cluster/class. We can easily recover the diversity within each cluster by computing different principal components and then sampling and generating accordingly. While the experiments presented here are somewhat limited in scale, we will explore more direct and powerful methods that utilize the learned data distributions and representations for conditional generation and estimation in the next chapter.

5.4 Summary and Notes
Historically, autoencoding has been one of the important drivers of research innovation in neural networks for learning, although the most practically impressive demonstrations of deep learning have probably been in other domains (such as discriminative classification, with AlexNet [KSH12], or generative modeling with GPT architectures [BMR+20]). Works we have featured throughout the chapter, especially the work of [HS06], served as catalysts of research interest in neural networks during times when they were otherwise not prominent in the machine learning research landscape. In modern practice, autoencoders remain core components of many large-scale systems for generating highly structured data such as visual data, speech data, and molecular data, especially the VQ-VAE approach [OVK17], which builds on the variational autoencoder methodology we discussed in Section 5.1.4. The core problem of autoencoding remains of paramount intellectual importance due to its close connection with representation learning, and we anticipate that it will reappear on the radar of practical researchers in the future as efficiency in training and deploying large models continues to become more important.
Materials presented in the second half of this chapter are based on a series of recent work on the topic of closed-loop transcription: [DTL+22], [PPC+23], [TDW+23], and [TDC+24]. In particular, Section 5.2.1 is based on the pioneering work of [DTL+22]. After that, the work of [PPC+23] has provided strong theoretical justifications for the closed-loop framework, at least for an ideal case. Section 5.3.1 and Section 5.3.2 are based on the works of [TDW+23] and [TDC+24], respectively. They demonstrate that the closed-loop framework naturally supports incremental and continuous learning, either in a class-wise or sample-wise setting. The reader may refer to these papers for more technical and experimental details.
Shallow vs. deep neural networks, for autoencoding and more.
In Section 5.1.2, we discussed Cybenko’s universal approximation theorem and how it states that in principle, a neural network with a single hidden layer (and suitable elementwise nonlinearities) is sufficient to approximate any suitably regular target function. Of course, in practice, the major architectural reason for the dominance of neural networks in practice has been the refinement of techniques for training deeper neural networks. Why is depth necessary? From a fundamental point of view, the issue of depth separations, which construct settings where a deeper neural network can approximate a given class of target functions with exponentially-superior efficiency relative to a shallow network, has been studied at great length in the theoretical literature: examples include [Tel16, BN20, VJO+21]. The ease of training deeper networks in practice has not received as satisfying an answer from the perspective of theory. ResNets [HZR+16a] represent the pioneering empirical work of making deeper networks more easily trainable, used in nearly all modern architectures in some form. Theoretical studies have focused heavily on trainability of very deep networks, quantified via the initial neural tangent kernel [BGW21, MBD+21], but these studies have not given significant insight into the trainability benefits of deeper networks in middle and late stages of training (but see [YH21] for the root of a line of research attempting to address this).
5.5 Exercises and Extensions
Exercise 5.1 (Conceptual Understanding of Manifold Flattening).
Consider data lying on a curved manifold embedded in (like a curved surface in -dimensional space), as discussed in the manifold flattening subsection of Section 5.1.2. In this exercise, we will describe the basic ingredients of the manifold flattening algorithm from [PPR+24]. A manifold is called flat if it is an open set in Euclidean space (or more generally, an open set in a subspace).
-
1.
Suppose the manifold is a graph: this means that (say), and that there is a function such that
(5.5.1) Give an integer and a map that flattens , and describe the corresponding (lossless) reconstruction procedure from the flattened representation.
-
2.
Now suppose that is a general smooth manifold. Smooth manifolds have the property that they are locally well-approximated by subspaces near each point. Describe in intuitive terms how to flatten the manifold locally at each point, by relating it to a graph. (The algorithm of [PPR+24] performs a refined version of this local flattening process in a way that allows them to be glued together to form a global flattening.)
Exercise 5.2 (Reproduce Closed-Loop Transcription).
Implement a closed-loop transcription pipeline for representation learning on the CIFAR-10 dataset following the methodology in Section 5.2.1. Reference [DTL+22] for useful hyperparameters and architecture settings. Reproduce the result in Figure 5.8.